浙江宁波宁波市2020年数学中考模拟试卷
试卷更新日期:2020-07-17 类型:中考模拟
一、选择题(共10小题,每小题4分,共40分)
-
1. -2020的倒数是( )A、 B、 C、2020 D、-20202. 代数式 在实数范围内有意义,则x的取值范围是( )A、x≠1 B、x≥1 C、x≤1 D、x≥-13. 如图所示,该几何体的左视图是( )
 A、
A、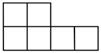 B、
B、 C、
C、 D、
D、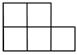 4. 不考虑颜色,对下图的对称性表述,正确的是( )
4. 不考虑颜色,对下图的对称性表述,正确的是( ) A、中心对称图形 B、轴对称图形 C、既是轴对称图形又是中心对称图形 D、既不是轴对称图形又不是中心对称图形5. 为了防控输入性“新冠肺炎”,某医院成立隔离治疗发热病人防控小组,决定从内科3位骨干医师中(含有甲)抽调2人组成.则甲一定会被抽调到防控小组的概率是( )A、 B、 C、 D、6. 明代大数学家程大位著《算法统宗》一书中,记载了这样一道数学题:“八万三千短竹竿,将来要把笔头安,管三套五为期定,问君多少能完成?”用现代的话说就是:有83000根短竹,每根短竹可制成毛笔的笔管3个或笔套5个,怎样安排笔管和笔套的短竹的数量,使制成的1个笔管与1个笔套正好配套?设用于制作笔管的短竹数为x根,用于制作笔套的短竹数为y根,则可列方程为( )A、 B、 C、 D、7. 如图,要焊接一个等腰三角形钢架,钢架的底角为35°,高CD长为3米,则斜梁AC的长为( )
A、中心对称图形 B、轴对称图形 C、既是轴对称图形又是中心对称图形 D、既不是轴对称图形又不是中心对称图形5. 为了防控输入性“新冠肺炎”,某医院成立隔离治疗发热病人防控小组,决定从内科3位骨干医师中(含有甲)抽调2人组成.则甲一定会被抽调到防控小组的概率是( )A、 B、 C、 D、6. 明代大数学家程大位著《算法统宗》一书中,记载了这样一道数学题:“八万三千短竹竿,将来要把笔头安,管三套五为期定,问君多少能完成?”用现代的话说就是:有83000根短竹,每根短竹可制成毛笔的笔管3个或笔套5个,怎样安排笔管和笔套的短竹的数量,使制成的1个笔管与1个笔套正好配套?设用于制作笔管的短竹数为x根,用于制作笔套的短竹数为y根,则可列方程为( )A、 B、 C、 D、7. 如图,要焊接一个等腰三角形钢架,钢架的底角为35°,高CD长为3米,则斜梁AC的长为( ) A、 B、 C、3sin 35° D、8. 已知函数y= ,下列说法:
A、 B、 C、3sin 35° D、8. 已知函数y= ,下列说法:①函数图象分布在第一、三象限;②在每个象限内,y随x的增大而减小;③若A(x1 , y1)、B(x2 , y2)两点在该图象上,且x1+x2=0,则y1=y2。其中说法正确的个数是( )
A、0 B、1 C、2 D、39. 八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线将这八个正方形分成面积相等的两部分,则直线l的解析式为( ) A、y=-x B、y= x C、y= x D、y= x10. 如图,正方形ABCD的边长AB=8,E为平面内一动点,且AE=4,F为CD上一点,CF=2,连接EF,ED,则2EF+ED的最小值为( )
A、y=-x B、y= x C、y= x D、y= x10. 如图,正方形ABCD的边长AB=8,E为平面内一动点,且AE=4,F为CD上一点,CF=2,连接EF,ED,则2EF+ED的最小值为( ) A、12 B、12 C、12 D、10
A、12 B、12 C、12 D、10二、填空题(共6小题,每小题5分,共30分)
-
11. 计算 的结果。12. 当前,新冠状性肺炎疫情已波及全世界200多个国家和地区,截止2020年5月12日14:00,全球确诊人数累计已达4175216人。下表是各大洲的确诊人数,则这组数据的中位数是。
地区
亚洲
欧洲
非洲
大洋洲
北美洲
南美洲
其他
现有确诊(人数)
279660
823853
40950
1300
1101631
190967
48
13. 若一元二次方程x²-2mx+m²=0的一根为x=-1,则m的值为。14. 如图,在平面坐标系中,点A是函数y= 图象上的点,过点A作x轴的垂线交x轴于点B,点C在y轴上,则△ABC的面积为。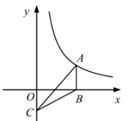 15. 如图,有一条长度为1的线段EF,其端点E、F分别在边长为3的正方形ABCD的四边上滑动。当EF绕着正方形的四边滑动一周时,EF的中点M形成的路径所围成的图形面积是。
15. 如图,有一条长度为1的线段EF,其端点E、F分别在边长为3的正方形ABCD的四边上滑动。当EF绕着正方形的四边滑动一周时,EF的中点M形成的路径所围成的图形面积是。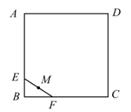 16. 一只电子跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后按图中箭头所示方向跳动,且每秒跳动一个单位,那么第2020秒时电子跳蚤所在位置的坐标是 。
16. 一只电子跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后按图中箭头所示方向跳动,且每秒跳动一个单位,那么第2020秒时电子跳蚤所在位置的坐标是 。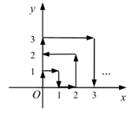
三、解答题(共8题,共80分)
-
17.(1)、解不等式组 ,并把解集在数轴上表示出来。(2)、先化简: ,再从-1≤x≤2的范围内选取一个合适的整数作为x的值代入求值。18. 某市教育局为了了解初一学生参加社会实践活动的天数,随机抽查本市部分初一学生非疫情期间参加社会实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图)。请你根据图中提供的信息,回答下列问题:
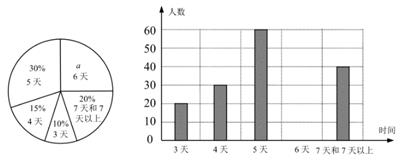 (1)、这次共抽取 ▲ 名学生进行统计调查,补全条形图;(2)、a= , 该扇形所对圆心角的度数为;(3)、如果该市有初一学生20000人,请你估计“活动时间不少于5天”的大约有多少人?19. 如图,在下列5×5的网格中,横、纵坐标均为整点的数叫做格点,例如(0,1)、B(2,1)、C(3,3)都是格点,现仅用无刻度的直尺在网格中做如下操作:
(1)、这次共抽取 ▲ 名学生进行统计调查,补全条形图;(2)、a= , 该扇形所对圆心角的度数为;(3)、如果该市有初一学生20000人,请你估计“活动时间不少于5天”的大约有多少人?19. 如图,在下列5×5的网格中,横、纵坐标均为整点的数叫做格点,例如(0,1)、B(2,1)、C(3,3)都是格点,现仅用无刻度的直尺在网格中做如下操作: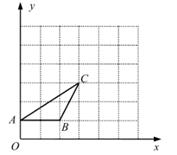
( 1 )直接写出点A关于点B旋转180°后对应点M的坐标 ▲ ;
( 2 )画出线段BE,使BE⊥AC,其中E是格点,并写出点E的坐标 ▲ ;
( 3 )找格点F,使∠EAF=∠CAB,画出∠EAF,并写出点F的坐标 ▲ 。
20. 为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行改建.如图,A、B两地之间有一座山。汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶。已知BC=80千米,∠A=45°,∠B=30°。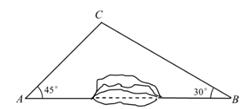 (1)、开通隧道前,汽车从A地到B地大约要走多少千米?(2)、开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据: ≈1.41, ≈1.73)21. 如图,△ABC中,∠C=90°,BD平分∠ABC,点O是边AB上一点,以点O为圆心,以OB为半径作圆,⊙O恰好经过点D。
(1)、开通隧道前,汽车从A地到B地大约要走多少千米?(2)、开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据: ≈1.41, ≈1.73)21. 如图,△ABC中,∠C=90°,BD平分∠ABC,点O是边AB上一点,以点O为圆心,以OB为半径作圆,⊙O恰好经过点D。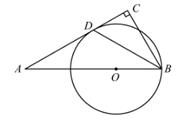 (1)、求证:直线AC是⊙O的切线;(2)、若∠A=30°,⊙O的半径是2,求线段CD的长。22. 为满足市场需求,某大型超市在端午节来临前夕,购进一种品牌的粽子,每袋进价是40元,超市规定每袋售价不得少于45元,根据以往销售经验发现:当售价定为每袋45元时,每天可以卖出700袋,每袋售价每提高1元,每天要少卖出20袋。(1)、试写出每天的销售利润P(元)与每袋涨价x(元)之间的函数关系式及自变量x的取值范围;(2)、当每袋涨价为多少元时,每天的销售利润P最大?最大利润是多少?(3)、如果超市想要每天获得不低于6000元的利润,请求出x的取值范围。23. 如图,已知二次函数的图象过点O(0,0),A(8,4),与x轴交于另一点B,且对称轴是直线x=3。
(1)、求证:直线AC是⊙O的切线;(2)、若∠A=30°,⊙O的半径是2,求线段CD的长。22. 为满足市场需求,某大型超市在端午节来临前夕,购进一种品牌的粽子,每袋进价是40元,超市规定每袋售价不得少于45元,根据以往销售经验发现:当售价定为每袋45元时,每天可以卖出700袋,每袋售价每提高1元,每天要少卖出20袋。(1)、试写出每天的销售利润P(元)与每袋涨价x(元)之间的函数关系式及自变量x的取值范围;(2)、当每袋涨价为多少元时,每天的销售利润P最大?最大利润是多少?(3)、如果超市想要每天获得不低于6000元的利润,请求出x的取值范围。23. 如图,已知二次函数的图象过点O(0,0),A(8,4),与x轴交于另一点B,且对称轴是直线x=3。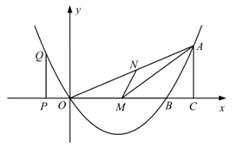 (1)、求该二次函数的解析式;(2)、若M是OB上的一点,作MN∥AB交OA于N,当△ANM面积最大时,求MN的长;(3)、P是x轴上的点,过P作PQ⊥x轴与抛物线交于Q,过A作AC⊥x轴于C(点P不与点C重合),当以O,P,Q为顶点的三角形与以O,A,C为顶点的三角形相似时,求P点的坐标。24. 如图,在菱形ABCD中,AB=α,∠ABC=60°,过点A作AE⊥BC,垂足为E,AF⊥CD,垂足为F。
(1)、求该二次函数的解析式;(2)、若M是OB上的一点,作MN∥AB交OA于N,当△ANM面积最大时,求MN的长;(3)、P是x轴上的点,过P作PQ⊥x轴与抛物线交于Q,过A作AC⊥x轴于C(点P不与点C重合),当以O,P,Q为顶点的三角形与以O,A,C为顶点的三角形相似时,求P点的坐标。24. 如图,在菱形ABCD中,AB=α,∠ABC=60°,过点A作AE⊥BC,垂足为E,AF⊥CD,垂足为F。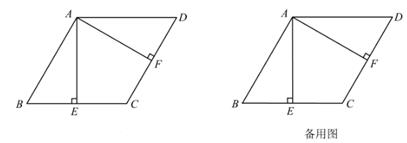 (1)、连接EF,用等式表示线段EF与EC的数量关系,并说明理由;(2)、连接BF,过点A作AK⊥BF,垂足为K,求BK的长(用含a的代数式表示);(3)、延长线段CB到G,延长线段DC到H,且BG=CH,连接AG、CH、AH
(1)、连接EF,用等式表示线段EF与EC的数量关系,并说明理由;(2)、连接BF,过点A作AK⊥BF,垂足为K,求BK的长(用含a的代数式表示);(3)、延长线段CB到G,延长线段DC到H,且BG=CH,连接AG、CH、AH①判断△AGH的形状,并说明理由;
②若a=2,S△ADH= (3+ ),求sin∠GAB的值。