2020年暑期衔接训练青岛版数学八年级下册：第13讲二次根式的性质

试卷更新日期：2020-07-17 类型：复习试卷

进入出卷网下载

一、单选题

1. 要使代数式 $\sqrt{2 x - 3}$ 有意义，则x的取值范围是（）

A、x> $\frac{3}{2}$ B、x＜ $\frac{3}{2}$ C、x≥ $\frac{3}{2}$ D、x≤ $\frac{3}{2}$

查看试题解析
2. 若 $\sqrt{（ a - 1)^{2}}$ =a-1，则（）

A、a<1 B、a≤1 C、a>1 D、a≥1

查看试题解析
3. 下列各式中① $\sqrt{a}$ ；② $\sqrt{b + 1}$ ；③ $\sqrt{a^{2}}$ ；④ $\sqrt{a^{2} + 3}$ ；⑤ $\sqrt{x^{2} - 1}$ ；⑥ $\sqrt{x^{2} + 2 x + 1}$ ，一定是二次根式的有（　　）个．

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 若 $\sqrt{a (5 - a)} = \sqrt{a} \cdot \sqrt{5 - a}$ ，则（）

A、a≤5 B、a≥0 C、0≤a≤5 D、a≥5

查看试题解析
5. 若 $\sqrt{(2 a - 1)^{2}} = 1 - 2 a$ ，则（）.

A、 $a < \frac{1}{2}$ B、 $a \leq \frac{1}{2}$ C、 $a > \frac{1}{2}$ D、 $a \geq \frac{1}{2}$

查看试题解析
6. 若x+y＝3+2 $\sqrt{2}$ ，x﹣y＝3﹣2 $\sqrt{2}$ ，则 $\sqrt{x^{2} - y^{2}}$ 的值为（）

A、4 $\sqrt{2}$ B、1 C、6 D、3﹣2 $\sqrt{2}$

查看试题解析
7. 小明的作业本上有以下四题：① $\sqrt{16 a^{4}}$ ＝4a²；② $\sqrt{5 a} \cdot \sqrt{10 a} = 5 \sqrt{2} a$ ；③ $a \sqrt{\frac{1}{a}} = \sqrt{a^{2} \cdot \frac{1}{a}} = \sqrt{a}$ ；④ $\sqrt{3 a} - \sqrt{2 a} = \sqrt{a}$ ，做错的题有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
8. 若a、b分别是6- $\sqrt{13}$ 的整数部分和小数部分，那么2a-b的值是（）

A、3- $\sqrt{3}$ B、4- $\sqrt{13}$ C、 $\sqrt{13}$ D、4+ $\sqrt{13}$

查看试题解析
9. 已知 $xy=3$ ，那么 $x \sqrt{\frac{y}{x}} + y \sqrt{\frac{x}{y}}$ 的值是（）

A、 $2 \sqrt{3}$ B、 $- 2 \sqrt{3}$ C、 $\pm 2 \sqrt{3}$ D、 $\pm \sqrt{3}$

查看试题解析
10. 已知：m， n是两个连续自然数（m<n），且q=mn，设p= $\sqrt{q + n} + \sqrt{q - m}$ 则p( )

A、总是奇数 B、总是偶数 C、有时奇数，有时偶数 D、有时有理数，有时无理数

查看试题解析

二、填空题

11. 能使等式 $\sqrt{\frac{x}{7 - x}} = \frac{\sqrt{x}}{\sqrt{7 - x}}$ 成立的x的取值范围是.

查看试题解析
12. 观察分析，探求规律，然后填空： $\sqrt{2}$ ， 2， $\sqrt{6}$ ， 2 $\sqrt{2}$ ， $\sqrt{10}$ ， …，（请在横线上写出第100个数）．

查看试题解析
13. 三角形的三边长分别为3、m、5，化简 $\sqrt{{(2 - m)}^{2}}$ ﹣ $\sqrt{{(m - 8)}^{2}}$ =

查看试题解析
14. 计算 $\sqrt{2026^{2} - 2026 + 4252 + 2127}$ = ．

查看试题解析
15. 化简 $m \sqrt{- \frac{1}{m}}$ 的结果为

查看试题解析
16. 当x=时，二次根式 $\sqrt{25 - {(2 + 3 x)}^{2}}$ 有最大值．

查看试题解析
17. 已知0＜a＜1，化简 $\sqrt{a + \frac{1}{a} + 2}$ - $\sqrt{a + \frac{1}{a} - 2}$ =

查看试题解析
18. 如图：A，B，C三点表示的数分别为a，b，c．
利用图形化简： $| a - b | - \sqrt{{(c - b)}^{2}} + \sqrt{{(a - c)}^{2}}$ = ．

查看试题解析

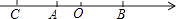
三、解答题

19. 计算：

(1)、 $2 \sqrt{12} + 3 \sqrt{1 \frac{1}{3}} - \sqrt{2} \times \sqrt{6}$

(2)、 $\sqrt{12} \div \sqrt{3} + | 2 - \sqrt{5} | - \frac{\sqrt{8} - \sqrt{6}}{\sqrt{2}}$

查看试题解析
20. 已知M= ${}^{m - 4}{\sqrt{m + 3}}$ 是m+3的算术平方根，N= ${}^{2 m - 4 n + 3}{\sqrt{n - 2}}$ 是n-2的立方根，求：M-N的值的平方根．

查看试题解析
21. 若a，b是一等腰三角形的两边长，且满足等式 $2 \sqrt{3 a - 6} + 3 \sqrt{2 - a} = b - 4$ ，试求此等腰三角形的周长．

查看试题解析
22. 已知实数a满足 $\sqrt{{(2008 - a)}^{2}}$ + $\sqrt{a - 2009}$ =a，求a﹣2008²的值是多少？

查看试题解析
23. 探索规律
先观察下列各式，再回答问题． $\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}}$ =1 $\frac{1}{2}$ ； $\sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}}$ =1 $\frac{1}{6}$ ； $\sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}}$ =1 $\frac{1}{12}$ ．
（1）根据上面三个等式提供的消息，请猜想 $\sqrt{1 + \frac{1}{4^{2}} + \frac{1}{5^{2}}}$ 的结果，不用验证；
（2）按照上面各等式反映的规律，试写出用含n的式子表示的等式（n为正整数），不用验证．

查看试题解析
24. 阅读下面材料，回答问题：
在化简 $\sqrt{5 - 2 \sqrt{6}}$ 的过程中，小张和小李的化简结果不同；

小张的化简如下： $\sqrt{5 - 2 \sqrt{6}} = \sqrt{2 - 2 \sqrt{2 \times 3} + 3} = \sqrt{{(\sqrt{2} - \sqrt{3})}^{2}} = \sqrt{2} - \sqrt{3}$ ；

小李的化简如下： $\sqrt{5 - 2 \sqrt{6}} = \sqrt{2 - 2 \sqrt{2 \times 3} + 3} = \sqrt{{(\sqrt{3} - \sqrt{2})}^{2}} = \sqrt{3} - \sqrt{2}$ ；

(1)、请判断谁的化简结果是正确，谁的化简结果是错误的，并说明理由．

(2)、请你利用上面所学的方法化简 $\sqrt{6 - 2 \sqrt{5}}$ ．

查看试题解析
25. 观察下列各式及其验证过程： $\sqrt{2 + \frac{2}{3}} = 2 \sqrt{\frac{2}{3}}$ ，验证： $\sqrt{2 + \frac{2}{3}} = \sqrt{\frac{8}{3}} = \sqrt{\frac{2^{2} \times 2}{3}} = 2 \sqrt{\frac{2}{3}}$ ． $\sqrt{3 + \frac{3}{8}} = 3 \sqrt{\frac{3}{8}}$ ，验证： $\sqrt{3 + \frac{3}{8}} = \sqrt{\frac{27}{8}} = \sqrt{\frac{3^{2} \times 3}{8}} = 3 \sqrt{\frac{3}{8}}$ ．
（1）按照上述两个等式及其验证过程，猜想 $\sqrt{4 + \frac{4}{15}}$ 的变形结果并进行验证．
（2）针对上述各式反映的规律，写出用a（a为任意自然数，且a≥2）表示的等式，并给出验证．
（3）针对三次根式及n次根式（n为任意自然数，且n≥2），有无上述类似的变形？如果有，写出用a（a为任意自然数，且a≥2）表示的等式，并给出验证．

查看试题解析

2020年暑期衔接训练青岛版数学八年级下册：第13讲 二次根式的性质

一、单选题

二、填空题

三、解答题

2020年暑期衔接训练青岛版数学八年级下册：第13讲二次根式的性质