2020年暑期衔接训练人教版数学七年级下册:第22讲 一元一次不等式组
试卷更新日期:2020-07-17 类型:复习试卷
一、单选题
-
1. 在平面直角坐标系中,若点P(m-3,m+1)在第三象限,则m的取值范围是( )A、-1<m<3 B、m>3 C、m<-1 D、m>-12. 若关于x的一元一次不等式组 的解集是 ,则a的取值范围是( )A、 B、 C、 D、3. 不等式组 的解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、 D、
D、 4. 不等式组 的解集是( )A、0<x≤2 B、0<x≤6 C、x>0 D、x≤25. 若关于x的不等式组 的解集为x<3,则k的取值范围为( )A、k>1 B、k<1 C、k≥1 D、k≤16. 如图,按下面的程序进行运算,规定程序运行到“判断结果是否大于30”为一次运算.若运算进行了3次才停止,则x的取值范围是( )
4. 不等式组 的解集是( )A、0<x≤2 B、0<x≤6 C、x>0 D、x≤25. 若关于x的不等式组 的解集为x<3,则k的取值范围为( )A、k>1 B、k<1 C、k≥1 D、k≤16. 如图,按下面的程序进行运算,规定程序运行到“判断结果是否大于30”为一次运算.若运算进行了3次才停止,则x的取值范围是( ) A、 B、 C、 D、7. 已知整数k使得关于x、y的二元一次方程组 的解为正整数,且关于x的不等式组 有且仅有四个整数解,则所有满足条件的k的和为( )
A、 B、 C、 D、7. 已知整数k使得关于x、y的二元一次方程组 的解为正整数,且关于x的不等式组 有且仅有四个整数解,则所有满足条件的k的和为( )
A、4 B、9 C、10 D、128. △ABC的两条高的长度分别为4和12,若第三条高也为整数,则第三条高的长度是( )
A、4 B、4或5 C、5或6 D、69. 公司计划用不超过500万元的资金购买单价分别为60万元、70万元的甲、乙两种设备.根据需要,甲种设备至少买3套,乙种设备至少买2套,则不同的购买方式共有( )种A、5 B、6 C、7 D、8二、填空题
-
10. 把一些书分给几名同学,如果每人分3本,那么余8本,如果前面的每名同学分5本,那么最后一人分不到3本,那么这些书共有本.11. 不等式组 的最小整数解为.12. 某校今年冬季烧煤取暖时间为4个月,如果每月比计划多烧5吨煤,那么取暖用煤总量将超过100吨;如果每月比计划少烧5吨,那么取暖用煤总量不足68吨,该校计划每月烧煤多少吨?设该校计划每月烧煤 吨,根据题意可列不等式组。13. 关于x的不等式组 的解集中至少有5个整数解,则正数a的最小值是.14. 已知
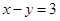 .①若 ,则 的取值范围是;②若 ,且 ,则 的取值范围是 .
.①若 ,则 的取值范围是;②若 ,且 ,则 的取值范围是 . 三、计算题
-
15. 解下面不等式组:(1)、(2)、(3)、
四、解答题
-
16. 解不等式组: ,并把解集表示在数轴上;17. 在今年年初,新型冠状病毒在武汉等地区肆虐,为了缓解湖北地区的疫情,全国各地的医疗队员都纷纷报名支援湖北,某方舱医院需要8组医护人员支援,要求每组分配的人数相同,若按每组人数比预定人数多分配1人,则总数会超过100人,若每组人数比预定人数少分配一人,则总数不够90人,那么预定每组分配的人数是多少人?18. 若关于x、y的二元一次方程组 的解满足 ,求出满足条件的m的所有整数的和
-