苏教版高中数学必修二1.1.1棱柱、棱锥、棱台

试卷更新日期：2020-07-16 类型：同步测试

进入出卷网下载

一、单选题

1. 下列几何体中是棱柱的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
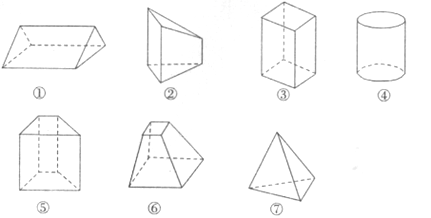
2. 如图所示的简单组合体的结构特征是（）

A、由两个四棱锥组合成的 B、由一个三棱锥和一个四棱锥组合成的 C、由一个四棱锥和一个四棱柱组合成的 D、由一个四棱锥和一个四棱台组合成的

查看试题解析
3. 下列说法中正确的是（）

A、棱柱的面中，至少有两个面互相平行 B、棱柱中两个互相平行的平面一定是棱柱的底面 C、棱柱中一条侧棱就是棱柱的高 D、棱柱的侧面一定是平行四边形，但它的底面一定不是平行四边形

查看试题解析
4. 如图所示，观察四个几何体，其中判断正确的是（）

A、①是棱台 B、②是圆台 C、③是棱锥 D、④不是棱柱

查看试题解析
5. 下列说法中正确的是（）

A、棱柱的面中，至少有两个面互相平行 B、棱柱的两个互相平行的平面一定是棱柱的底面 C、棱柱的一条侧棱的长叫做棱柱的高 D、棱柱的侧面是平行四边形，但它的底面一定不是平行四边形

查看试题解析
6. 有一长方体木块，其顶点为 $A B C D - A_{1} B_{1} C_{1} D_{1}$ ， $A B = 3$ ， $B C = 2$ ， $A A_{1} = 1$ ，一小虫从长方体木块的一顶点A绕其表面爬行到另一顶点 $C_{1}$ ，则小虫爬行的最短距离为 $($ $)$

A、 B、 C、 $2 \sqrt{5}$ D、

查看试题解析
7. 下列三种叙述，正确的有（）
①用一个平面去截棱锥，棱锥底面和截面之间的部分是棱台；
②两个底面平行且相似，其余各面都是梯形的多面体是棱台；
③有两个面互相平行，其余四个面都是等腰梯形的六面体是棱台．

A、0个 B、1个 C、2个 D、3个

查看试题解析
8. 下列说法错误的是（）

A、多面体至少有四个面 B、九棱柱有9条侧棱，9个侧面，侧面为平行四边形 C、长方体、正方体都是棱柱 D、三棱柱的侧面为三角形

查看试题解析
9. 下列关于棱柱的说法中，错误的是（）

A、三棱柱的底面为三角形 B、一个棱柱至少有五个面 C、若棱柱的底面边长相等，则它的各个侧面全等 D、五棱柱有5条侧棱、5个侧面，侧面为平行四边形

查看试题解析
10. 对有两个面互相平行，其余各面都是梯形的多面体，以下说法正确的是（）

A、棱柱 B、棱锥 C、棱台 D、一定不是棱柱、棱锥

查看试题解析
11. 下列命题正确的是( )

A、有两个面平行，其余各面都是四边形的几何体叫棱柱. B、有两个面平行，其余各面都是平行四边形的几何体叫棱柱. C、有两个面平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱. D、用一个平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台.

查看试题解析
12. 如图所示，在棱长为 $6$ 的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，点 $E ， F$ 分别是棱 $C_{1} D_{1} ， B_{1} C_{1}$ 的中点，过 $A ， E ， F$ 三点作该正方体的截面，则截面的周长为（）

A、 $18 + 3 \sqrt{2}$ B、 $6 \sqrt{13} + 3 \sqrt{2}$ C、 $6 \sqrt{5} + 9 \sqrt{2}$ D、 $10 + 3 \sqrt{2} + 4 \sqrt{10}$

查看试题解析
13. 下列结论正确的是（）

A、各个面都是三角形的几何体是三棱锥 B、一平面截一棱锥得到一个棱锥和一个棱台 C、棱锥的侧棱长与底面多边形的边长相等，则该棱锥可能是正六棱锥 D、圆锥的顶点与底面圆周上的任意一点的连线都是母线

查看试题解析
14. 下列关于棱锥、棱台的说法，其中不正确的是（）

A、棱台的侧面一定不会是平行四边形 B、棱锥的侧面只能是三角形 C、由四个面围成的封闭图形只能是三棱锥 D、棱锥被平面截成的两部分不可能都是棱锥

查看试题解析
15. 有下列说法：
①有两个面互相平行，其余各面都是平行四边形的几何体的侧棱一定不相交于一点，故一定不是棱台；②两个互相平行的面是平行四边形，其余各面是四边形的几何体不一定是棱台；③两个互相平行的面是正方形，其余各面是四边形的几何体一定是棱台．
其中正确的说法的序号有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
16. 给出下列命题中正确的是（　　）

A、棱柱被平面分成的两部分可以都是棱柱 B、底面是矩形的平行六面体是长方体 C、棱柱的底面一定是平行四边形 D、棱锥的底面一定是三角形

查看试题解析
17. 下列说法正确的是（）

A、在圆柱的上、下底面的圆周上各取一点，则这两点的连线是圆柱的母线； B、底面为正多边形，且有相邻两个侧面与底面垂直的棱柱是正棱柱； C、棱台的上、下底面可以不相似，但侧棱长一定相等． D、以直角三角形的一边所在直线为轴旋转所得的旋转体是圆锥．

查看试题解析
18. 棱台不具有的性质是（　　）

A、两底面相似 B、侧面都是梯形 C、侧棱都平行 D、侧棱延长后都交于一点

查看试题解析

二、填空题

19. 一个棱柱有10个顶点，所有侧棱长的和为60，则每条侧棱长为.

查看试题解析
20. 如图，在棱长为2的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $E$ 、 $F$ 分别为棱 $A_{1} D_{1}$ 、 $C_{1} D_{1}$ 的中点， $N$ 是线段 $B C_{1}$ 上的点，且 $B N = \frac{1}{4} B C_{1}$ ，若 $P$ 、 $M$ 分别为线段 $D_{1} B$ 、 $E F$ 上的动点，则 $| P M | + | P N |$ 的最小值为．

查看试题解析

三、解答题

21. 如图，在边长为2a的正方形ABCD中，E，F分别为AB，BC的中点，沿图中虚线将3个三角形折起，使点A，B，C重合，重合后记为点P.
问：

(1)、折起后形成的几何体是什么几何体？

(2)、这个几何体共有几个面，每个面的三角形有何特点？

(3)、每个面的三角形面积为多少？

查看试题解析
22. 如图，正方体ABCD－A₁B₁C₁D₁的棱长为a ， M为BD₁的中点，N在A₁C₁上，且满足|A₁N|＝3|NC₁|.

(1)、求MN的长；

(2)、试判断△MNC的形状．

查看试题解析