苏教版高中数学必修一3.4.1函数与方程
试卷更新日期:2020-07-16 类型:同步测试
一、单选题
-
1. 函数 的零点所在的区间是( )A、
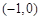 B、
B、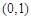 C、
C、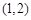 D、
D、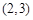 2. 函数 的零点所在区间为 ( )A、
2. 函数 的零点所在区间为 ( )A、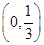 B、
B、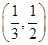 C、
C、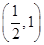 D、
D、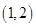 3. 函数 的零点所在的区间是( )A、 B、 C、 D、4. 函数 的零点所在的一个区间是( )A、 B、 C、 D、5. 设a,b∈R , 函数f(x)= ,若函数y=f(x)-ax-b恰有3个零点,则( )A、a<-1,b<0 B、a<-1,b>0 C、 a>-1,b>0 D、a>-1,b>06. 若函数f(x)=alog2(|x|+4)+x2+a2﹣8有唯一的零点,则实数a的值是( )A、﹣4 B、2 C、±2 D、﹣4或27. 已知函数 ,若函数 有两个不同的零点,则 的取值范围( )A、 B、
3. 函数 的零点所在的区间是( )A、 B、 C、 D、4. 函数 的零点所在的一个区间是( )A、 B、 C、 D、5. 设a,b∈R , 函数f(x)= ,若函数y=f(x)-ax-b恰有3个零点,则( )A、a<-1,b<0 B、a<-1,b>0 C、 a>-1,b>0 D、a>-1,b>06. 若函数f(x)=alog2(|x|+4)+x2+a2﹣8有唯一的零点,则实数a的值是( )A、﹣4 B、2 C、±2 D、﹣4或27. 已知函数 ,若函数 有两个不同的零点,则 的取值范围( )A、 B、 C、
C、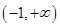 D、
D、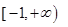 8. 已知函数f(x)=丨x﹣2丨+1,g(x)=kx.若方程f(x)=g(x)有两个不相等的实根,则实数k的取值范围是( )A、(0, ) B、( ,1) C、(1,2) D、(2,+∞)9. 用二分法找函数f(x)=2x+3x﹣7在区间[0,4]上的零点近似值,取区间中点2,则下一个存在零点的区间为( )A、(0,1) B、(0,2) C、(2,3) D、(2,4)10. 方程 的解所在区间是( )A、
8. 已知函数f(x)=丨x﹣2丨+1,g(x)=kx.若方程f(x)=g(x)有两个不相等的实根,则实数k的取值范围是( )A、(0, ) B、( ,1) C、(1,2) D、(2,+∞)9. 用二分法找函数f(x)=2x+3x﹣7在区间[0,4]上的零点近似值,取区间中点2,则下一个存在零点的区间为( )A、(0,1) B、(0,2) C、(2,3) D、(2,4)10. 方程 的解所在区间是( )A、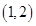 B、
B、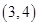 C、
C、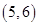 D、
D、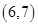 11. 已知函数f(x)=ax3﹣3x2+1,若f(x)存在唯一的零点x0 , 且x0>0,则实数a的取值范围是( )A、(1,+∞) B、(2,+∞) C、(﹣∞,﹣1) D、(﹣∞,﹣2)12. 实数a,b定义运算“ ”; ,设 ,若函数 至少有两个零点,则k的取值范围是( )A、 B、 C、 D、
11. 已知函数f(x)=ax3﹣3x2+1,若f(x)存在唯一的零点x0 , 且x0>0,则实数a的取值范围是( )A、(1,+∞) B、(2,+∞) C、(﹣∞,﹣1) D、(﹣∞,﹣2)12. 实数a,b定义运算“ ”; ,设 ,若函数 至少有两个零点,则k的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 函数 的零点个数是;其所有零点之和为 .14. 函数f(x)=ax2+2ax+c(a≠0)的一个零点为1,则它的另一个零点为 .15. 设 是定义在R上的两个周期函数, 的周期为4, 的周期为2,且 是奇函数.当 时, , ,其中k>0.若在区间(0,9]上,关于x的方程 有8个不同的实数根,则k的取值范围是.16. 已知函数 ,若函数 有两不同的零点,则实数 的取值范围是 .17. 已知 ,函数 若关于 的方程 恰有2个互异的实数解,则 的取值范围是.18. 已知函数f(x)=kx,g(x)= ,如果关于x的方程f(x)=g(x)在区间[ ,e]内有两个实数解,那么实数k的取值范围是 .
三、解答题
-
19. 已知函数 的零点是 和 ,求函数 的零点.20. 已知函数 有两个零点.(1)、若函数的两个零点是 和 ,求 的值;(2)、若函数的两个零点是 和 ,求 的取值范围.21. 已知函数 .(1)、证明 有且只有一个零点;(2)、求这个零点所在的一个区间,使这个区间的长度不大于 .22. 已知函数 .(1)、若f(x)是定义在R上的偶函数,求实数a的值;(2)、在(1)的条件下,若g(x)=f(x)﹣2,求函数g(x)的零点.