上海市长宁区2020年中考数学二模试卷

试卷更新日期：2020-07-16 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列实数中，无理数是（）

A、 $0$ B、 $\sqrt{3}$ C、 $- 3$ D、 $\sqrt{9}$

查看试题解析
2. 下列单项式中，与 $x y^{2}$ 是同类项的是（）

A、 $x^{2} y$ B、 $x^{2} y^{2}$ C、 $2 x y^{2}$ D、 $3 x y$

查看试题解析
3. 关于反比例函数 $y = \frac{2}{x}$ ，下列说法错误的是（）

A、点 $(- 2, - 1)$ 在它的图像上 B、它的图像在第一、三象限 C、它的图像关于原点中心对称 D、 $y$ 的值随着 $x$ 的值的增大而增大

查看试题解析
4. 如图是关于某班同学一周体育锻炼情况的统计图，那么该班学生这一周参加体育锻炼时间的众数、中位数分别是（）

A、 $8$ 、 $9$ B、 $8$ 、 $8.5$ C、 $16$ 、 $8.5$ D、 $16$ 、 $14$

查看试题解析
5. 如果两圆的半径长分别为 $5$ 和 $3$ ，圆心距为 $7$ ，那么这两个圆的位置关系是（）

A、内切 B、外离 C、相交 D、外切

查看试题解析
6. ▱ABCD中，E，F是对角线BD上不同的两点，下列条件中，不能得出四边形AECF一定为平行四边形的是（）

A、BE=DF B、AE=CF C、AF//CE D、∠BAE=∠DCF

查看试题解析

二、填空题

7. 计算： ${(x^{3})}^{2} \div {(- x)}^{2} =$ ．

查看试题解析
8. 方程 $\sqrt{3 - x} = 2$ 的根为．

查看试题解析
9. 不等式组 ${\begin{array}{l} 3 x + 4 \geq 0 \\ \frac{1}{2} x - 2 \leq 1 \end{array}$ 的解集是．

查看试题解析
10. 已知正三角形的边心距为 $1$ ，那么它的边长为．

查看试题解析
11. 如果抛物线 $y = (a - 1) x^{2} - 1$ （ $a$ 为常数）不经过第二象限，那么 $a$ 的取值范围是．

查看试题解析
12. 如果关于 $x$ 的多项式 $x^{2} - 2 x + m$ 在实数范围内因式分解，那么实数 $m$ 的取值范围是．

查看试题解析
13. 从1，2，3，4四个数中任意取出2个数做加法，其和为偶数的概率是．

查看试题解析
14. 我国古代数学著作《九章算术》中有一道阐述“盈不足术”的问题，原文是“今有人共买物，人出八，盈三；人出七，不足四，问人数、物价各几何？大致意思是：“现有几个人共同购买一个物品，每人出 $8$ 元，则多 $3$ 元；每人出 $7$ 元，则差 $4$ 元．问人数、物品的价格各是多少？”如果设共有 $x$ 人，物品的价格为 $y$ 元，那么根据题意可列出方程组为．

查看试题解析
15. 已知甲乙两位运动员在一次射击训练中各打五发，成绩的平均环数相同，甲的方差为 $1.6$ ；乙的成绩（环）为 $7$ 、 $8$ 、 $10$ 、 $6$ 、 $9$ ，那么这两位运动员中的成绩较稳定（填“甲”或“乙”）

查看试题解析
16. 如图，已知在 $Δ A B C$ 中，点 $D$ 在边 $A C$ 上， $A D = 2 D C$ ， $\vec{A B} = \vec{a}$ ， $\vec{A C} = \vec{b}$ ，那么 $\vec{B D} =$ （用含向量 $\vec{a}$ ， $\vec{b}$ 的式子表示）

查看试题解析
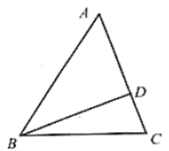17. 如果一个四边形有且只有三个顶点在圆上，那么称这个四边形是该圆的“联络四边形”，已知圆的半径长为 $5$ ，这个圆的一个联络四边形是边长为 $2 \sqrt{5}$ 的菱形，那么这个菱形不在圆上的顶点与圆心的距离是．

查看试题解析
18. 如图，已知在 $Δ A B C$ 中， $∠ C = 90 °$ ， $B C = 2$ ，点 $D$ 是边 $B C$ 的中点， $∠ A B C = ∠ C A D$ ，将 $Δ A C D$ 沿直线 $A D$ 翻折，点 $C$ 落在点 $E$ 处，联结 $B E$ ，那么线段 $B E$ 的长为．

查看试题解析

三、解答题

19. 计算： $\sqrt{4 \frac{1}{2}} + 2^{\frac{1}{2}} + {(\sqrt{2} + 1)}^{- 1} + {(\sqrt{2} - 1)}^{0}$

查看试题解析
20. 解方程： $\frac{x}{x + 3} - \frac{6}{9 - x^{2}} = \frac{1}{x - 3}$

查看试题解析
21. 如图，在梯形 $A B C D$ 中， $A D / / B C$ ， $A D = 2$ ， $B C = 5$ ， $∠ B A C = 45 °$ ， $\cos ∠ A C B = \frac{3}{5}$ ．

(1)、求线段 $A C$ 的长；

(2)、联结 $B D$ ，交对角线 $A C$ 于点 $O$ ，求 $∠ A D O$ 的余切值．

查看试题解析
22. 如图反映了甲、乙两名自行车爱好者同时骑车从 $A$ 地到 $B$ 地进行训练时行驶路程 $y$ （千米）和行驶时间 $x$ （小时）之间关系的部分图像，根据图像提供的信息，解答下列问题：

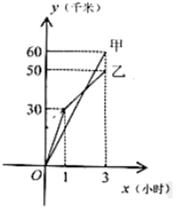(1)、求乙的行驶路程 $y$ 和行驶时间 $x$ $(1 \leq x \leq 3)$ 之间的函数解析式；

(2)、如果甲的速度一直保持不变，乙在骑行 $3$ 小时之后又以第 $1$ 小时的速度骑行，结果两人同时到达 $B$ 地，求 $A$ 、 $B$ 两地之间的距离．

查看试题解析
23. 如图，已知四边形 $A B C D$ 是矩形，点 $E$ 在对角线 $A C$ 上，点 $F$ 在边 $C D$ 上（点 $F$ 与点 $C$ 、 $D$ 不重合）， $B E ⊥ E F$ ，且 $∠ A B E + ∠ C E F = 45 °$ ．

(1)、求证：四边形 $A B C D$ 是正方形；

(2)、联结 $B D$ ，交 $E F$ 于点 $Q$ ，求证： $D Q \cdot B C = C E \cdot D F$ ．

查看试题解析
24. 如图，在平面直角坐标系 $x O y$ 中，已知抛物线 $y = x^{2} + m x + n$ 经过点 $A (2 ， - 2)$ ，对称轴是直线 $x = 1$ ，顶点为点 $B$ ，抛物线与 $y$ 轴交于点 $C$ ．

(1)、求抛物线的表达式和点 $B$ 的坐标；

(2)、将上述抛物线向下平移 $1$ 个单位，平移后的抛物线与 $x$ 轴正半轴交于点 $D$ ，求 $Δ B C D$ 的面积；

(3)、如果点 $P$ 在原抛物线上，且在对称轴的右侧，联结 $B P$ 交线段 $O A$ 于点 $Q$ ， $\frac{B Q}{P Q} = \frac{1}{5}$ ，求点 $P$ 的坐标．

查看试题解析
25. 已知 $A B$ 是 $⊙ O$ 的一条弦，点 $C$ 在 $⊙ O$ 上，联结 $CO$ 并延长，交弦 $A B$ 于点 $D$ ，且 $C D = C B$ ．

(1)、如图1，如果 $B O$ 平分 $∠ A B C$ ，求证： $A B = B C$ ；

(2)、如图2，如果 $A O ⊥ O B$ ，求 $A D ： D B$ 的值；

(3)、延长线段 $A O$ 交弦 $B C$ 于点 $E$ ，如果 $Δ E O B$ 是等腰三角形，且 $⊙ O$ 的半径长等于 $2$ ，求弦 $B C$ 的长．

查看试题解析