上海市嘉定区2020年中考数学二模试卷

试卷更新日期：2020-07-16 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列四个选项，其中的数不是分数的选项是(　　)

A、﹣4 $\frac{1}{2}$ B、 $\frac{22}{7}$ C、 $\frac{π}{2}$ D、50%

查看试题解析
2. 当x≠0时，下列运算正确的是(　　)

A、x³+x²=x⁵ B、x³•x²=x⁶ C、(x³)²=x⁹ D、x³÷x²=x

查看试题解析
3. 下列关于二次函数y=x²﹣3的图象与性质的描述，错误的是(　　)

A、该函数图象的开口向上 B、函数值y随着自变量x的值的增大而增大 C、该函数图象关于y轴对称 D、该函数图象可由函数y=x²的图象平移得到

查看试题解析
4. 一组数据3，4，4，5，若添加一个数4，则发生变化的统计量是（）

A、平均数 B、众数 C、中位数 D、方差

查看试题解析
5. 下列图形，是轴对称图形但不是中心对称图形的是(　　)

A、线段 B、矩形 C、等腰梯形 D、圆

查看试题解析
6. 下列四个命题中，真命题是(　　)

A、一组对边平行，一条对角线被另一条对角线平分的四边形是平行四边形 B、一组对角相等，一条对角线被另一条对角线平分的四边形是平行四边形 C、一组邻边相等，一条对角线被另一条对角线平分的四边形是平行四边形 D、一组对边相等，一条对角线被另一条对角线平分的四边形是平行四边形

查看试题解析

二、填空题

7. 化简 $\frac{2}{x} + \frac{3}{x} =$ ．

查看试题解析
8. 函数y $= \frac{1}{2 x + 3}$ 的定义域是．

查看试题解析
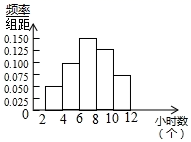
9. 分解因式4x²﹣4x+1＝.

查看试题解析
10. 方程 $\sqrt{x - 2} =$ 3的根是．

查看试题解析
11. 如果反比例函数y $= \frac{k}{x}$ (k≠0)的图象经过点P(1，3)，那么当x＜0时，函数值y随自变量x的值的增大而(从“增大”或“减小”中选择)．

查看试题解析
12. 一个不透明的布袋中有2个红球和4个黑球，它们除颜色外其他都相同，那么从该布袋中随机取出1个球恰好是红球的概率为．

查看试题解析
13. 半径长为2的半圆的弧长为(计算结果保留π)．

查看试题解析
14. 为了调查A学校2400名学生的某一周阅读课外书籍的时间t(单位：时)，一个数学课外活动小组随机调查了A学校120名学生该周阅读课外书籍的时间t(单位：时)，并绘制成如图所示的频率分布直方图(列频数分布表时，执行了“每个小组可含最小值，不含最大值”的约定)．请根据以上信息，估计A学校该周阅读课外书籍的时间位于8≤t＜10之间的学生人数大约为人．

查看试题解析
15. 如图，在正六边形ABCDEF中，如果向量 $\vec{A B} = \vec{a}$ ， $\vec{A F} = \vec{b}$ ，那么向量 $\vec{A D}$ 用向量 $\vec{a}$ ， $\vec{b}$ 表示为．

查看试题解析
16. 如图，点A、B、C在⊙O上，其中点C是劣弧 $\hat{A B}$ 的中点．请添加一个条件，使得四边形AOBC是菱形，所添加的这个条件可以是(使用数学符号语言表达)．

查看试题解析
17. 七巧板由五个等腰直角三角形与两个平行四边形(其中的一个平行四边形是正方形)组成．用七巧板可以拼出丰富多彩的图形，图中的正方形ABCD就是由七巧板拼成的，那么正方形EFGH的面积与正方形ABCD的面积的比值为．

查看试题解析
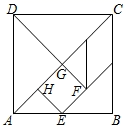18. 定义：如果三角形的两个内角∠α与∠β满足∠α=2∠β，那么，我们将这样的三角形称为“倍角三角形”．如果一个等腰三角形是“倍角三角形”，那么这个等腰三角形的腰长与底边长的比值为．

查看试题解析

三、解答题

19. 计算： $| \sqrt{3} - 1 | - \sqrt{2} \cdot \sqrt{6} + {(\sqrt{3} + 1)}^{2} - {(\sqrt{3})}^{2}$ ．

查看试题解析
20. 解方程： $\frac{x + 2}{x - 2} - \frac{16}{x^{2} - 4} = \frac{1}{x + 2}$ ．

查看试题解析
21. 如图所示的方格纸是由9个大小完全一样的小正方形组成的．点A、B、C、D均在方格纸的格点(即图中小正方形的顶点)上，线段AB与线段CD相交于点E．设图中每个小正方形的边长均为1．

(1)、求证：AB⊥CD；

(2)、求sin∠BCD的值．

查看试题解析
22. 已知汽车燃油箱中的y(单位：升)与该汽车行驶里程数x(单位：千米)是一次函数关系．贾老师从某汽车租赁公司租借了一款小汽车，拟去距离出发地600公里的目的地旅游(出发之前，贾老师往该汽车燃油箱内注满了油)．行驶了200千米之后，汽车燃油箱中的剩余油量为40升；又行驶了100千米，汽车燃油箱中的剩余油量为30升．

(1)、求y关于x的函数关系式(不要求写函数的定义域)；

(2)、当汽车燃油箱中的剩余油量为8升的时候，汽车仪表盘上的燃油指示灯就会亮起来．在燃油指示灯亮起来之前，贾老师驾驶该车可否抵达目的地？请通过计算说明．

查看试题解析
23. 已知：△ABC，AB=AC，∠BAC=90°，点D是边BC的中点，点E在边AB上(点E不与点A、B重合)，点F在边AC上，联结DE、DF．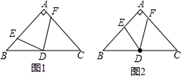

(1)、如图1，当∠EDF=90°时，求证：BE=AF；

(2)、如图2，当∠EDF=45°时，求证： $\frac{D E^{2}}{D F^{2}} = \frac{B E}{C F}$ ．

查看试题解析
24. 在平面直角坐标系xOy中（如图），已知经过点A（﹣3，0）的抛物线y＝ax²+2ax﹣3与y轴交于点C，点B与点A关于该抛物线的对称轴对称，D为该抛物线的顶点．

(1)、直接写出该抛物线的对称轴以及点B的坐标、点C的坐标、点D的坐标；

(2)、联结AD、DC、CB，求四边形ABCD的面积；

(3)、联结AC．如果点E在该抛物线上，过点E作x轴的垂线，垂足为H，线段EH交线段AC于点F．当EF＝2FH时，求点E的坐标．

查看试题解析
25. 如图，在△ABC中，∠C=90°，AB=5cm，cosB $= \frac{4}{5}$ ．动点D从点A出发沿着射线AC的方向以每秒1cm的速度移动，动点E从点B出发沿着射线BA的方向以每秒2cm的速度移动．已知点D和点E同时出发，设它们运动的时间为t秒．联结BD．

(1)、当AD=AB时，求tan∠ABD的值；

(2)、以A为圆心，AD为半径画⊙A；以点B为圆心、BE为半径画⊙B．讨论⊙A与⊙B的位置关系，并写出相对应的t的值．

(3)、当△BDE为直角三角形时，直接写出tan∠CBD的值．

查看试题解析