黑龙江省哈尔滨市2020年中考数学4月模拟试卷

试卷更新日期：2020-07-16 类型：中考模拟

进入出卷网下载

一、单选题

1. 如果|x|＝|－5|，那么x等于（）

A、5 B、－5 C、＋5或－5 D、以上都不对

查看试题解析
2. 下列运算正确的是（）

A、2x²＋x²＝3x⁴ B、x³y·（－3x²）＝－3x⁵y C、（2x³－x²－x）÷（－x）＝－2x²＋x D、（x－y）²＝x²－y²

查看试题解析
3. 下列图案中，既是中心对称图形又是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
4. 如图是由5个完全相同的小正方形搭成的几何体，如果将小正方体A放到小正方体B的正上方，则它的（）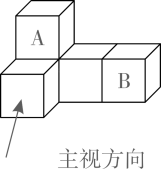

A、主视图会发生改变 B、俯视图会发生改变 C、左视图会发生改变 D、三种视图都会发生改变

查看试题解析
5. 把抛物线y=﹣2x²先向右平移1个单位长度，再向上平移2个单位长度后，所得函数的表达式为（　　）

A、y=﹣2（x+1）²+2 B、y=﹣2（x+1）²﹣2 C、y=﹣2（x﹣1）²+2 D、y=﹣2（x﹣1）²﹣2

查看试题解析
6. 如图，AB和AC与圆O分别相切于点B和点C，点D是圆O上一点，若∠BAC＝74°，则∠BDC等于（　　）

A、46° B、53° C、74° D、106°

查看试题解析
7. 分式方程 $\frac{x - 5}{x - 1} + \frac{2}{x} = 1$ 的解为（）

A、 $x = - 1$ B、 $x = 1$ C、 $x = 2$ D、 $x = - 2$

查看试题解析
8. 若函数y＝ $\frac{m - 3}{x}$ 的图象在第一、三象限内，则m的取值范围是（　　）

A、m＞﹣3 B、m＜﹣3 C、m＞3 D、m＜3

查看试题解析
9. 如图，在菱形ABCD中，对角线AC、BD相交于点O，BD＝24，tan∠ABD＝ $\frac{3}{4}$ ，则线段AB的长为（　　）

A、9 B、12 C、15 D、18

查看试题解析
10. 如图，抛物线y＝a（x+3）（x﹣k）交x轴于点A、B，（A左B右），交y轴于点C，△AOC的周长为12，sin∠CBA＝ $\frac{\sqrt{5}}{5}$ ，则下列结论：①A点坐标（﹣3，0）；②a＝﹣ $\frac{1}{6}$ ；③点B坐标（8，0）；④对称轴x＝ $\frac{5}{2}$ ．其中正确的有（　　）个．

A、4 B、3 C、2 D、1

查看试题解析

二、填空题

11. 港珠澳大桥被英国《卫报》誉为“新世界七大奇迹”之一，它是世界总体跨度最长的跨海大桥，全长55000米.数字55000用科学记数法表示为.

查看试题解析
12. 若代数式 $\frac{\sqrt{1 - x}}{x}$ 有意义，则x的取值范围是.

查看试题解析
13. 分解因式6xy²－9x²y－y³ = .

查看试题解析
14. 对于有理数 $m$ ，我们规定 $[m]$ 表示不大于 $m$ 的最大整数，例如： $[1, 2] = 1$ ， $[3] = 3$ ， $[- 2.5] = - 3$ ，若 $[\frac{x + 2}{3}] = - 5$ ，则整数x的取值是．

查看试题解析
15. 计算 $\sqrt{32} - 4 \sqrt{\frac{1}{8}}$ 的结果是．

查看试题解析
16. 如图，在 $△ A B C$ 中， $∠ A C B = 90^{°}$ ，且 $A C = B C$ .点D是 $△ A B C$ 内的一点，将 $△ A C D$ 以点C为中心顺时针旋转 $90^{°}$ 得到 $△ B C E$ ，若点A、D、E共线，则 $∠ A E B$ 的度数为.

查看试题解析
17. 盒子中装有2个红球和4个绿球，每个球除颜色外都相同，从盒子中任意摸出一个球，是绿球的概率是．

查看试题解析
18. 某扇形的弧长为πcm，面积为3πcm² ，则该扇形的半径为cm

查看试题解析
19. 在⊙O中，若一条弦AB的长等于这个圆的半径，则这条弦AB所对的圆周角是（注意：有两种情况，可不要少填哟！）

查看试题解析
20. 如图，在边长为6的等边△ABC中，AD是BC边上的中线，点E是△ABC内一个动点，且DE＝2，将线段AE绕点A逆时针旋转60°得到AF，则DF的最小值是．

查看试题解析

三、解答题

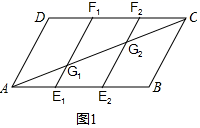
21. 先化简，再求代数式 $\frac{a - 3}{2 a - 4} \div (\frac{5}{a - 2} - a - 2)$ 的值，其中a＝tan60°﹣6sin30°.

查看试题解析
22.

(1)、如图1，在平行四边形ABCD中，点E₁ ， E₂是AB三等分点，点F₁ ， F₂是CD三等分点，E₁F₁ ， E₂F₂分别交AC于点G₁ ， G₂ ，求证：AG₁＝G₁G₂＝G₂C．

(2)、如图2，由64个边长为1的小正方形组成的一个网格图，线段MN的两个端点在格点上，请用一把无刻度的尺子，画出线段MN三等分点P，Q．(保留作图痕迹)

查看试题解析
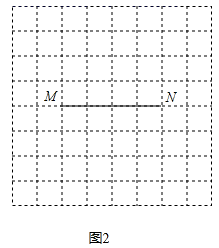23. 某校为了解本校八年级学生数学学习情况，随机抽查该年级若干名学生进行测试，然后把测试结果分为4个等级：A、B、C、D，并将统计结果绘制成两幅不完整的统计图，请根据图中的信息解答下列问题

(1)、补全条形统计图

(2)、等级为D等的所在扇形的圆心角是度

(3)、如果八年级共有学生1800名，请你估算我校学生中数学学习A等和B等共多少人？

查看试题解析
24. 如图，在△ABC中，∠ABC＝90°，AB＝BC，三角形的顶点在相互平行的三条直线l₁ ， l₂ ， l₃上，且l₁ ， l₂之间的距离为2，l₂ ， l₃之间的距离为3，BC交l₂于D点．

(1)、求AB的长．

(2)、求sin∠BAD的值．

查看试题解析
25. 有一段6000米的道路由甲乙两个工程队负责完成．已知甲工程队每天完成的工作量是乙工程队每天完成工作量的2倍，且甲工程队单独完成此项工程比乙工程队单独完成此项工程少用10天．

(1)、求甲、乙两工程队每天各完成多少米？

(2)、如果甲工程队每天需工程费7000元，乙工程队每天需工程费5000元，若甲队先单独工作若干天，再由甲乙两工程队合作完成剩余的任务，支付工程队总费用不超过79000元，则两工程队最多可以合作施工多少天？

查看试题解析
26. 如图，四边形ABCD为菱形，以AD为直径作⊙O交AB于点F，连接DB交⊙O于点H，E是BC上的一点，且BE＝BF，连接DE．

(1)、求证：△DAF≌△DCE．

(2)、求证：DE是⊙O的切线．

(3)、若BF＝2，DH＝ $\sqrt{5}$ ，求四边形ABCD的面积．

查看试题解析
27. 如图1，直线l：y＝ $\frac{1}{2}$ x+2与x轴交于点A，与y轴交于点B．已知点C（﹣2，0）．

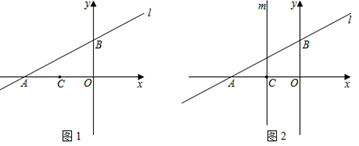(1)、求出点A，点B的坐标．

(2)、P是直线AB上一动点，且△BOP和△COP的面积相等，求点P坐标．

(3)、如图2，平移直线l，分别交x轴，y轴于交于点A₁ ， B₁ ，过点C作平行于y轴的直线m，在直线m上是否存在点Q，使得△A₁B₁Q是等腰直角三角形？若存在，请直接写出所有符合条件的点Q的坐标．

查看试题解析