广东省湛江市2020年中考数学二模试卷
试卷更新日期:2020-07-16 类型:中考模拟
一、单选题
-
1. 在数轴上表示数-1和2018的两点分别为A和B,则A,B两点之间的距离为( )A、2017 B、2018 C、2019 D、20202. 用百度搜索关键词“十九大”,百度为我们找到相关结果约18 600 000个,把18 600 000这个数用科学记数法表示为( )A、0.186×108 B、1.86×107 C、18.6×106 D、186×1053. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
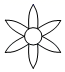 B、
B、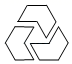 C、
C、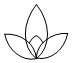 D、
D、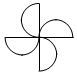 4. 如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是( )
4. 如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是( )
A、30° B、40° C、50° D、60°5. 下列说法正确的是( )A、鞋店老板比较关心的是一周内卖出的鞋的尺码组成的一组数据的众数 B、某种彩票的中奖率是2%,则买50张这种彩票一定会中奖 C、“打开电视,正在播放《新闻联播》”是必然事件 D、若甲组数据方差S甲2=0.06,乙组数据的方差S乙2=0.1,则乙组数据比甲组数据稳定6. 如图,D是△ABC内一点,BD⊥CD,E、F、G、H分别是边AB、BD、CD、AC的中点.若AD=10,BD=8,CD=6,则四边形EFGH的周长是( )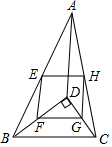 A、24 B、20 C、12 D、107. 如图,在矩形ABCD中,点A的坐标是(﹣1,0),点C的坐标是(2,4),则BD的长是( )
A、24 B、20 C、12 D、107. 如图,在矩形ABCD中,点A的坐标是(﹣1,0),点C的坐标是(2,4),则BD的长是( ) A、6 B、5 C、3 D、48. 如图,AB是⊙O直径,若∠AOC=140°,则∠D的度数是( )
A、6 B、5 C、3 D、48. 如图,AB是⊙O直径,若∠AOC=140°,则∠D的度数是( ) A、20° B、30° C、40° D、70°9. 若a≠b,且 则 的值为( )A、 B、1 C、.4 D、310. 如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )
A、20° B、30° C、40° D、70°9. 若a≠b,且 则 的值为( )A、 B、1 C、.4 D、310. 如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( ) A、
A、 B、
B、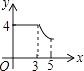 C、
C、 D、
D、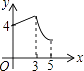
二、填空题
-
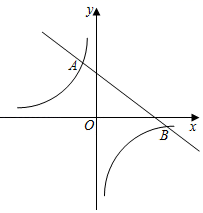
11. 分解因式6xy2-9x2y-y3 = .12. 如果a+3和2a﹣6是一个数的平方根,这个数为 .13. 分式方程 = 的解为.14. 已知圆锥的底面半径为3,母线长为7,则圆锥的侧面积是.15. 如图,反比例函数y1= 与一次函数y2=mx+b(m≠0)的交点为A(﹣1,4.5),B(3,﹣1.5),当y1≥y2时,写出自变量x的取值范围 .
 16. 如果a是不为1的有理数,我们把 称为a的差倒数,如:2的差倒数是 ,-1的差倒数是 ,已知 , 是 的差倒数, 是 的差倒数, 是 的差倒数,…,依此类推,则 .17. 如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N.下列结论:①△APE≌△AME;②PM+PN=AC;③△POF∽△BNF;④当△PMN∽△AMP时,点P是AB的中点,其中一定正确的结论有 . (填上所有正确的序号).
16. 如果a是不为1的有理数,我们把 称为a的差倒数,如:2的差倒数是 ,-1的差倒数是 ,已知 , 是 的差倒数, 是 的差倒数, 是 的差倒数,…,依此类推,则 .17. 如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N.下列结论:①△APE≌△AME;②PM+PN=AC;③△POF∽△BNF;④当△PMN∽△AMP时,点P是AB的中点,其中一定正确的结论有 . (填上所有正确的序号).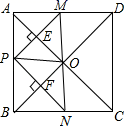
三、解答题
-
18. 计算: .19. 先化简,再求值: ,其中 .20. 如图,正方形网格中的两个小正方形的边长都是 ,每个小正方形的顶点叫格点,一个顶点为格点的三角形称为格点三角形:
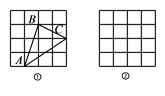 (1)、如图①,已知格点 ,则 (是或不是)直角三角形:(2)、画一个格点 ,使其为钝角三角形,且面积为21. 某初中学校餐厅为了解学生对早餐的要求,随即抽样调查了该校的部分学生,并根据其中两个单选问题的调查结果,绘制了如下尚不完整的统计图表.
(1)、如图①,已知格点 ,则 (是或不是)直角三角形:(2)、画一个格点 ,使其为钝角三角形,且面积为21. 某初中学校餐厅为了解学生对早餐的要求,随即抽样调查了该校的部分学生,并根据其中两个单选问题的调查结果,绘制了如下尚不完整的统计图表.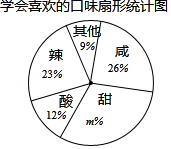
学生能接受的早餐价格统计表
价格分组(单位:元)
频数
频率
0<x≤2
60
0.15
2<x≤4
180
c
4<x≤6
92
0.23
6<x≤8
a
0.12
x>8
20
0.05
合计
b
1
根据以上信息解答下列问题:
(1)、统计表中,a= , b= , c= .(2)、扇形统计图中,m的值为 , “甜”所对应的圆心角的度数是 .(3)、该餐厅计划每天提供早餐2000份,其中咸味大约准备多少份较好?22. 某电器超市销售每台进价分别为2000元、1700元的A、B两种型号的空调,如表是近两周的销售情况:销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
5台
18000元
第二周
4台
10台
31000元
(进价、售价均保持不变,利润=销售总收入进货成本)
(1)、求A、B两种型号的空调的销售单价;(2)、若超市准备用不多于54000元的金额再采购这两种型号的空调共30台,求A种型号的空调最多能采购多少台?23. 矩形ABCD的对角线相交于点O.DE∥AC,CE∥BD. (1)、求证:四边形OCED是菱形;(2)、若∠ACB=30°,菱形OCED的面积为 ,求AC的长.24. 如图,⊙O的直径AB=26,P是AB上(不与点A、B重合)的任一点,点C、D为⊙O上的两点,若∠APD=∠BPC,则称∠CPD为直径AB的“回旋角”.
(1)、求证:四边形OCED是菱形;(2)、若∠ACB=30°,菱形OCED的面积为 ,求AC的长.24. 如图,⊙O的直径AB=26,P是AB上(不与点A、B重合)的任一点,点C、D为⊙O上的两点,若∠APD=∠BPC,则称∠CPD为直径AB的“回旋角”.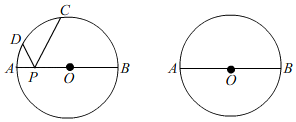 (1)、若∠BPC=∠DPC=60°,则∠CPD是直径AB的“回旋角”吗?并说明理由;(2)、若 的长为 π,求“回旋角”∠CPD的度数;(3)、若直径AB的“回旋角”为120°,且△PCD的周长为24+13 ,直接写出AP的长.25. 如图,在平面直角标系中,抛物线C:y= 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为y轴正半轴上一点.且满足OD= OC,连接BD,
(1)、若∠BPC=∠DPC=60°,则∠CPD是直径AB的“回旋角”吗?并说明理由;(2)、若 的长为 π,求“回旋角”∠CPD的度数;(3)、若直径AB的“回旋角”为120°,且△PCD的周长为24+13 ,直接写出AP的长.25. 如图,在平面直角标系中,抛物线C:y= 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为y轴正半轴上一点.且满足OD= OC,连接BD,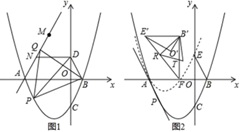 (1)、如图1,点P为抛物线上位于x轴下方一点,连接PB,PD,当S△PBD最大时,连接AP,以PB为边向上作正△BPQ,连接AQ,点M与点N为直线AQ上的两点,MN=2且点N位于M点下方,连接DN,求DN+MN+ AM的最小值(2)、如图2,在第(1)问的条件下,点C关于x轴的对称点为E,将△BOE绕着点A逆时针旋转60°得到△B′O′E′,将抛物线y= 沿着射线PA方向平移,使得平移后的抛物线C′经过点E,此时抛物线C′与x轴的右交点记为点F,连接E′F,B′F,R为线段E’F上的一点,连接B′R,将△B′E′R沿着B′R翻折后与△B′E′F重合部分记为△B′RT,在平面内找一个点S,使得以B′、R、T、S为顶点的四边形为矩形,求点S的坐标.
(1)、如图1,点P为抛物线上位于x轴下方一点,连接PB,PD,当S△PBD最大时,连接AP,以PB为边向上作正△BPQ,连接AQ,点M与点N为直线AQ上的两点,MN=2且点N位于M点下方,连接DN,求DN+MN+ AM的最小值(2)、如图2,在第(1)问的条件下,点C关于x轴的对称点为E,将△BOE绕着点A逆时针旋转60°得到△B′O′E′,将抛物线y= 沿着射线PA方向平移,使得平移后的抛物线C′经过点E,此时抛物线C′与x轴的右交点记为点F,连接E′F,B′F,R为线段E’F上的一点,连接B′R,将△B′E′R沿着B′R翻折后与△B′E′F重合部分记为△B′RT,在平面内找一个点S,使得以B′、R、T、S为顶点的四边形为矩形,求点S的坐标.