广东省深圳市光明区2020年中考数学一模试卷
试卷更新日期:2020-07-16 类型:中考模拟
一、单选题
-
1. 下列四个数中,最大的负数是( )A、-1 B、-2020 C、0 D、20202. 如图的五个甲骨文中,既不是轴对称图形,也不是中心对称图形的有( )
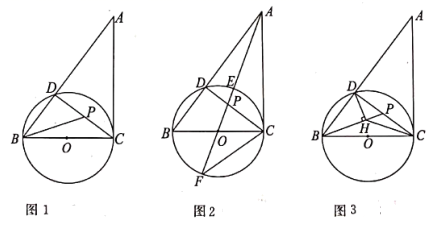
 A、1个 B、2个 C、3个 D、4个3. 自教育部开展“停课不停学”工作以来,截至2020年4月3日,参加在线课程学习的学生达11.8亿人次,将11.8亿用科学记数法表示为( )A、 B、 C、 D、4. 图中所示的几何体的左视图为( )
A、1个 B、2个 C、3个 D、4个3. 自教育部开展“停课不停学”工作以来,截至2020年4月3日,参加在线课程学习的学生达11.8亿人次,将11.8亿用科学记数法表示为( )A、 B、 C、 D、4. 图中所示的几何体的左视图为( )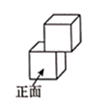 A、
A、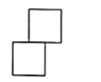 B、
B、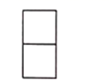 C、
C、 D、
D、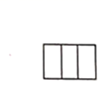 5. 数据1,3,6,5,3,6,8,6的中位数、众数分别为( )A、5.5,6 B、6,5.5 C、6,3 D、5,66. 如图, , , ,则 ( )
5. 数据1,3,6,5,3,6,8,6的中位数、众数分别为( )A、5.5,6 B、6,5.5 C、6,3 D、5,66. 如图, , , ,则 ( ) A、 B、 C、 D、7. 下列运算正确的是( )A、 B、 C、 D、8. 疫情期间居民为了减少外出时间,更愿意使用 在线上买菜,某买菜 今年一月份新进册用户为200万,三月份新注册用户为338万,则二、三两个月新注册用户每月平均增长率是( )A、10% B、15% C、23% D、30%9. 如图,在 中, , 是 的中点,以点 为圆心,大于点E到 的距离为半径画弧,两弧相交于点F,射线 分别与BD, 交于点G,H,若 , ,则 的长为( )
A、 B、 C、 D、7. 下列运算正确的是( )A、 B、 C、 D、8. 疫情期间居民为了减少外出时间,更愿意使用 在线上买菜,某买菜 今年一月份新进册用户为200万,三月份新注册用户为338万,则二、三两个月新注册用户每月平均增长率是( )A、10% B、15% C、23% D、30%9. 如图,在 中, , 是 的中点,以点 为圆心,大于点E到 的距离为半径画弧,两弧相交于点F,射线 分别与BD, 交于点G,H,若 , ,则 的长为( ) A、 B、5 C、 D、1010. 如图,两个三角形纸板 , 能完全重合, , , ,将 绕点 从重合位置开始,按逆时针方向旋转,边 , 分别与 , 交于点 , (点 不与点 , 重合),点 是 的内心,若 ,点 运动的路径为 ,则图中阴影部分的面积为( )
A、 B、5 C、 D、1010. 如图,两个三角形纸板 , 能完全重合, , , ,将 绕点 从重合位置开始,按逆时针方向旋转,边 , 分别与 , 交于点 , (点 不与点 , 重合),点 是 的内心,若 ,点 运动的路径为 ,则图中阴影部分的面积为( )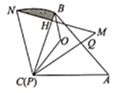 A、 B、 C、 D、11. 二次函数 的图象如图所示,下列结论:
A、 B、 C、 D、11. 二次函数 的图象如图所示,下列结论:① ;② ;③ ;④ .其中正确结论的个数是( )
 A、1 B、2 C、3 D、412. 如图,在正方形 中, 的顶点 , 分别在 , 边上,高 与正方形的边长相等,连接 分别交 , 于点 , ,下列说法:① ;②连接 , ,则 为直角三角形;③ ;④若 , ,则 的长为 ,其中正确结论的个数是( )
A、1 B、2 C、3 D、412. 如图,在正方形 中, 的顶点 , 分别在 , 边上,高 与正方形的边长相等,连接 分别交 , 于点 , ,下列说法:① ;②连接 , ,则 为直角三角形;③ ;④若 , ,则 的长为 ,其中正确结论的个数是( ) A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
13. 分解因式: =;14. 在一个不透明的袋子里装有独立包装的口罩,其中粉色口罩有3个、蓝色口罩有2个,这些口罩除了颜色外全部相同,从中随机依次不放回拿出两个口罩,则两个口罩都是粉色的概率是 .15. 已知 , (其中 和 都表示角度),比如求 ,可利用公式得 ,又如求 ,可利用公式得 ,请你结合材料,若 ( 为锐角),则 的度数是 .16. 如图,把一块含30°角的三角板的直角顶点放在反比例函数y=- (x<0)的图象上的点C处,另两个顶点分别落在原点O和x轴的负半轴上的点A处,且∠CAO=30°,则AC边与该函数图象的另一交点D的坐标为 .

三、解答题
-
17. 计算:18. 先化简: ,再从 的整数中选取一个合适的x的值代入求值.19. 复课返校后,为了让同学们进一步了解“新型冠状病毒”的防控知识,某学校组织了一次关于“新型冠状病毒”的防控知识比赛,从问卷中随机抽查了一部分,对调查结果进行了分组统计,并制作了如下表格与条形统计图:
分组结果
频数
频率
A.完全掌握
30
0.3
B.比较清楚
50
C.不怎么清楚
0.15
D.不清楚
5
0.05

请根据上图完成下面题目:
(1)、总人数为人, , ;(2)、请你补全条形统计图;(3)、若全校有2700人,请你估算一下全校对“新型冠状病毒”的防控知识“完全掌握”的人数有多少.20. 随着疫情逐步得到控制,在疫情防控初期驰援武汉的医护人员已陆续返回,深圳市为返深医护人员在中心区亮灯致敬.某大厦的立面截图如图所示,图中的所有点都在同一平面内,已知高度为 的测量架 在 点处测得 ,将测量架沿 方向前进 到达 点,在 点处测得 ,电子显示屏的底端 与地面的距离 ,请你计算电子显示屏 的高度.(结果精确到1m,其中: , ) 21. 复课返校后,为了拉大学生锻炼的间距,学校决定增购适合独立训练的两种体育器材:跳绳和毽子.如果购进5根跳绳和6个毽子共需196元;购进2根跳绳和5个键子共需120元.(1)、求一根跳绳和一个毽子的售价分别是多少元;(2)、学校计划购买跳绳和键子两种器材共400个,由于受疫情影响,商场决定对这两种器材打折销售,其中跳绳以八折出售,毽子以七五折出售,学校要求跳绳的数量不少于毽子数量的3倍,跳绳的数量不多于310根,请你求出学校花钱最少的购买方案.
21. 复课返校后,为了拉大学生锻炼的间距,学校决定增购适合独立训练的两种体育器材:跳绳和毽子.如果购进5根跳绳和6个毽子共需196元;购进2根跳绳和5个键子共需120元.(1)、求一根跳绳和一个毽子的售价分别是多少元;(2)、学校计划购买跳绳和键子两种器材共400个,由于受疫情影响,商场决定对这两种器材打折销售,其中跳绳以八折出售,毽子以七五折出售,学校要求跳绳的数量不少于毽子数量的3倍,跳绳的数量不多于310根,请你求出学校花钱最少的购买方案.