2020年暑期衔接训练青岛版数学八年级下册：第12讲 第八章《一元一次不等式》单元测试
试卷更新日期：2020-07-16 类型：复习试卷
一、单选题
-
1. 下面给出了五个式子：①5＞0，②3x+y＞0，③x+3≤3，④a﹣1，⑤x≠3；其中不等式有（ ）A、2个 B、3个 C、4个 D、5个2. 若关于x的一元一次不等式组 的解是x＜7，则m的取值范围是（ ）A、m≤7 B、m＜7 C、m≥7 D、m＞73. 关于x的不等式组 有5个整数解，则a的取值范围是（ ）A、1＜a≤2 B、1＜a＜2 C、1≤a＜2 D、﹣1≤a＜04. 下列不等式变形错误的是（ ）A、若 a＞b，则 1﹣a＜1﹣b B、若 a＜b，则 ax2≤bx2 C、若 ac＞bc，则 a＞b D、若 m＞n，则 ＞5. 关于x的不等式组 无解，则a的取值范围是（ ）A、a> B、a≥ C、a< D、a≤6. 甲在集市上先买了 只羊，平均每只 元，稍后又买了 只，平均每只羊 元，后来他以每只 元的价格把羊全卖给了乙，结果发现赔了钱，赔钱的原因是（ ）A、 B、 C、 D、与 、 大小无关7.
设“●”“▲”“■”表示三种不同的物体，现用天平称称了两次，情况如图所示，那么●▲■这三种物体按质量从大到小的顺序排列（ ）
A、■●▲ B、■▲● C、▲●■ D、▲■●8. 若方程组的解满足0＜x+y＜1，则k的取值范围是（ ）
A、-4＜k＜1 B、-4＜k＜0 C、0＜k＜9 D、k＞-49. 用长为40 m的铁丝围成如图所示的图形，一边靠墙，墙的长度AC=30 m，要使靠墙的一边长不小于25 m，那么与墙垂直的一边长x(m)的取值范围为（ ）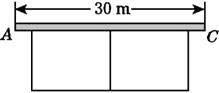
A、0≤x≤5 B、x≥ C、0≤x≤ D、 ≤x≤510. 用锤子以相同的力将铁钉垂直钉入木块，随着铁钉的深入，铁钉所受的阻力也越来越大.当未进入木块的钉子长度足够时，每次钉入木块的钉子长度是前一次的 .已知这个铁钉被敲击3次后全部进入木块(木块足够厚)，且第一次敲击后铁钉进入木块的长度是2 cm，若铁钉总长度为a cm，则a满足（ ）
A、2.5<a<4 B、2.5≤a<3.5 C、3≤a<4 D、3<a≤3.511. 若[m]表示不大于m的最大整数，例如：[5]=5，[﹣3，6]=﹣4，则关于x的方程[ ﹣5]=7的整数解有（ ）A、1个 B、2个 C、3个 D、4个12. 某种肥皂原零售价每块2元，凡购买2块以上（包括2块），商场推出两种优惠销售办法.第一种：一块肥皂按原价，其余按原价的七折销售；第二种：全部按原价的八折销售.你在购买相同数量肥皂的情况下，要使第一种方法比第二种方法得到的优惠多，最少需要买（ ）块肥皂.
A、5 B、4 C、3 D、2二、填空题
-
13.
若
是关于 
的一元一次不等式，则 的取值是。14. 某校今年冬季烧煤取暖时间为4个月，如果每月比计划多烧5吨煤，那么取暖用煤总量将超过100吨；如果每月比计划少烧5吨，那么取暖用煤总量不足68吨，该校计划每月烧煤多少吨？设该校计划每月烧煤 吨，根据题意可列不等式组。15. 如图，在平面直角坐标系中，点M是直线y=﹣x上的动点，过点M作MN⊥x轴，交直线y=x于点N，当MN≤8时，设点M的横坐标为m，则m的取值范围为 ．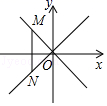
16. 某中学有若干间学生宿舍,若每间宿舍住4人,则有20人没有宿舍住;若每间住8人,则有一间宿舍住不满也不空,则住宿舍的学生人数17. 如果关于 的不等式组 整数解仅有 那么适合这个不等式组的整数 组成的有序数对 共有对.18. 对一个实数x按如图所示的程序进行操作，规定：程序运行从“输入一个实数x”到：“判断结果是否大于190？”为一次操作．如果操作只进行一次就停止，则x的取值范围是 ．
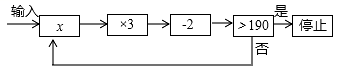19. 我们把 称为二阶行列式，规定它的运算法则为 ，例如 ，如果 ，则 的解集是.20. 一个长方形的两边分别为xcm和20cm，如果它的周长小于120cm面积大于200cm2 ， 则x的取值范围是三、解答题
-
21. 解不等式:22. 解不等式组 ，并将其解集表示在如图所示的数轴上．
23. 某公交公司有A，B型两种客车，它们的载客量和租金如下表：A
B
载客量（人/辆）
45
30
租金（元/辆）
400
280
红星中学根据实际情况，计划租用A，B型客车共5辆，同时送七年级师生到基地参加社会实践活动，设租用A型客车x辆，根据要求回答下列问题：
(1)、用含x的式子填写下表：车辆数（辆）
载客量
租金（元）
A
x
B
(2)、若要保证租车费用不超过1900元，求x的最大值.24. 我县“果菜大王”王大炮收货番茄20吨，青椒12吨．现计划租用甲、乙两种货车共8辆将这批果菜全部运往外地销售，已知一辆甲种货车可装番茄4吨和青椒1吨，一辆乙种货车可装番茄和青椒各2吨．(1)、王灿有几种方案安排甲、乙两种货车可一次性地将果菜运到销售地？(2)、若甲种货车每辆要付运输费300元，乙种货车每辆要付运输费240元，则果农王大炮应选择哪种方案，使运输费最少？最少运费是多少？25. 某小区积极创建环保示范社区，决定在小区内安装垃圾分类的温馨提示牌和垃圾箱，已知温馨提示牌的单价为每个30元，垃圾箱的单价为每个90元，共需购买温馨提示牌和垃圾箱共100个.(1)、若规定温馨提示牌和垃圾箱的个数之比为1:4，求所需的购买费用；(2)、若该小区至多安放48个温馨提示牌，且费用不超过6300元，请列举所有购买方案，并说明理由.26. 宁波某企业新增了一个化工项目，为了节约资源，保护环境，该企业决定购买A、B两种型号的污水处理设备共10台，具体情况如下表：A型
B型
价格（万元/台）
15
12
月污水处理能力（吨/月）
250
200
经预算，企业最多支出136万元购买设备，且要求月处理污水能力不低于2150吨．
(1)、该企业有哪几种购买方案？(2)、哪种方案更省钱？并说明理由．27. 为了提倡低碳环保，北仑区某公司决定购买10台节省能源的新设备，现有甲、乙两种型号的设备可供选购，经调查：购买3台甲型设备比购买2台乙型设备多花16万元，购买2台甲型设备比购买3台乙型设备少花6万元。(1)、求甲、乙两种型号设备的价格；(2)、该公司经预算决定购买节省能源的新设备的资金不超过110万元，你认为该公司共有几种购买方案；(3)、在（2）的条件下，已知甲型设备的产量为240吨/月，乙型设备的产量为180吨/月，若每月要求总产量不低于2040吨，为了节约资金，请你为该公司设计一种最省钱的购买案。