初中数学浙教版八年级上册1.3 证明 同步训练
试卷更新日期:2020-07-15 类型:同步测试
一、单选题
-
1. 以下判断正确的是( )A、三角形的一个外角等于两个内角的和 B、三角形的外角大于任何一个内角 C、一个三角形中,至少有一个角大于或等于60° D、三角形的外角是内角的邻补角2. 如图,将一张含有30°角的三角形纸片的两个顶点叠放在矩形的两条对边上,若∠2=44°,则∠1的大小为( )
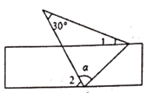 A、14° B、16° C、90°-α D、α-44°3. AD是∠CAE的平分线,∠B=35°,∠DAE=60°,则∠ACD= ( )
A、14° B、16° C、90°-α D、α-44°3. AD是∠CAE的平分线,∠B=35°,∠DAE=60°,则∠ACD= ( )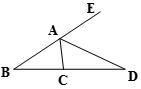 A、25° B、60° C、85° D、95°4. 已知, ,判断 之间的关系满足( )
A、25° B、60° C、85° D、95°4. 已知, ,判断 之间的关系满足( )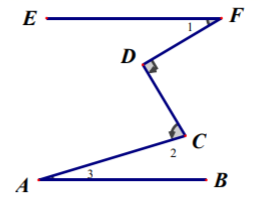 A、 B、 C、 D、5. 如图所示,两条直线AB、CD被第三条直线EF所截,∠1=75°,下列说法正确的( )
A、 B、 C、 D、5. 如图所示,两条直线AB、CD被第三条直线EF所截,∠1=75°,下列说法正确的( ) A、若∠4=75°,则AB∥CD B、若∠4=105°,则AB∥CD C、若∠2=75°,则AB∥CD D、若∠2=155°,则AB∥CD6. 下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容。
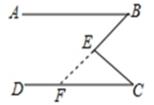
A、若∠4=75°,则AB∥CD B、若∠4=105°,则AB∥CD C、若∠2=75°,则AB∥CD D、若∠2=155°,则AB∥CD6. 下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容。已知:如图,∠BEC=∠B+∠C
求证:AB∥CD
证明:延长BE交※于点F,
则∠BEC=180°-∠FEC=◎+∠C
又∠BEC=∠B+∠C,得∠B=▲
故AB∥CD(@相等,两直线平行)
则回答正确的是( )
A、◎代表∠FEC B、@代表同位角 C、▲代表∠EFC D、※代表AB二、填空题
-
7. 如图所示,边长为1正方形网格中,点A、B、C落在格点上,则 的度数为 .
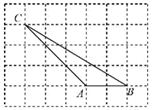 8. 小明在玩“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题,如图,若AB∥CD,∠BAE=92°,∠DCE=121°,则∠AEC=°。
8. 小明在玩“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题,如图,若AB∥CD,∠BAE=92°,∠DCE=121°,则∠AEC=°。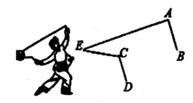 9. 一个零件的形状如图所示,按规定∠A应等于90°,∠B、∠C应分别是21°和32°.当检验工人量得的∠BDC的度数不等于度时,就可判定此零件不合格?
9. 一个零件的形状如图所示,按规定∠A应等于90°,∠B、∠C应分别是21°和32°.当检验工人量得的∠BDC的度数不等于度时,就可判定此零件不合格? 10. 如图,给出下列三个论断:①∠B+∠D=180°;②AB∥CD;③BC∥DE.请你以其中两个论断作为已知条件,填入“已知”栏中,以一个论断作为结论,填入“结论栏中,使之成为一道由已知可得到结论的题目,并说明理由.
10. 如图,给出下列三个论断:①∠B+∠D=180°;②AB∥CD;③BC∥DE.请你以其中两个论断作为已知条件,填入“已知”栏中,以一个论断作为结论,填入“结论栏中,使之成为一道由已知可得到结论的题目,并说明理由.
已知,如图, ,
结论: .
理由: .
11. 如图,在 中, , 和 的平分线交于点 ,得 ; 和 的平分线交于点 ,得 和 的平分线交于点 ,则 度. 12. 请在括号内填写下列证明过程的依据:
12. 请在括号内填写下列证明过程的依据:已知:如图,在△ABC中,CH是外角∠ACD的平分线,BH是∠ABC 的平分线。

求证:∠A=2∠H
证明:∵∠ACD是∠ABC的一个外角,
∴∠ACD=∠ABC+∠A
∠2是△BCH的一个外角,
∠2=∠1+∠H(理由同上)
∵CH是外角∠ACD的平分线,BH是∠ABC的平分线
∴∠1= ∠ABC,∠2= ∠ACD
∴∠A=∠ACD-∠ABC=2(∠2-∠1) (等式的性质)
而∠H=∠2-∠1 (等式的性质)
∴∠A=2∠H
三、解答题
-
13. 如图,点D、E在AB上点F在BC上,点G在AC上,∠1=∠B,∠2=∠3,∠4=80°,求∠ADC的度数.
 14. 已知:如图,在△ABC中,AD∥BC,AD平分外角∠EAC,求证:∠B=∠C.
14. 已知:如图,在△ABC中,AD∥BC,AD平分外角∠EAC,求证:∠B=∠C. 15. 阅读并填空.已知:如图,线 、线 是直线, .试说明 .
15. 阅读并填空.已知:如图,线 、线 是直线, .试说明 .
解: (已知)
()
(已知)
()
(已知)
()
即
()
()
16.(1)、中德关系源远流长,中德经济合作广泛。如图1,是德国较早进入中国内地的汽车公司品牌奔驰的标志.已知A、B、D是圆上的三点,O是圆心
求证:∠ACB=∠AOB+∠CBO+∠CAO。
(2)、如图2,CE和BD相交于点O,若∠EOD=140°,求∠A+∠B+∠C+∠D+∠E+∠F的度数。

