湖北省荆州市松滋市2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2020-07-15 类型：期末考试

进入出卷网下载

一、选择题

1. $\sqrt{1 - m}$ 有意义，m的取值范围是（）

A、m≤0 B、m﹤1 C、m≤1 D、m≥1

查看试题解析
2. 空气是由多种气体混合而成的，为了简明扼要的介绍空气的组成情况，较好的描述数据，最适合使用的统计图是（）

A、扇形图 B、条形图 C、折线图 D、直方图

查看试题解析
3. 下列命题为真命题的是（）

A、同位角相等 B、4的平方根是2 C、经过直线外一点，有且只有一条直线与这条直线平行 D、直线外一点到直线上的某一点的线段长度，叫点到直线的距离

查看试题解析
4. 不等式组 ${\begin{array}{l} - x < 3 ， \\ 2 x - 1 \leq 3 \end{array}$ 的解集在数轴上表示正确的是(　　)

A、 B、 C、 D、

查看试题解析
5. 若将点A（1，3）向左平移2个单位，再向下平移4个单位得到点B，则点B的坐标为（）

A、（﹣1，0） B、（﹣1，﹣1） C、（﹣2，0） D、（﹣2，﹣1）

查看试题解析
6. 为了绿化校园，30名学生共种78棵树苗，其中男生每人种3棵，女生每人种2棵，设男生有x人，女生有y人，根据题意，所列方程组正确的是（）

A、 ${\begin{matrix} x + y = 78 \\ 3 x + 2 y = 30 \end{matrix}$ B、 ${\begin{matrix} x + y = 78 \\ 2 x + 3 y = 30 \end{matrix}$ C、 ${\begin{matrix} x + y = 30 \\ 2 x + 3 y = 78 \end{matrix}$ D、 ${\begin{matrix} x + y = 30 \\ 3 x + 2 y = 78 \end{matrix}$

查看试题解析
7. 如图，直线l₁∥l₂ ， ∠1=20°，则∠2+∠3等于（）

A、150° B、165° C、180° D、200°

查看试题解析
8. 如图，将直角三角形ABC沿斜边BC所在直线向右平移一定的长度得到三角形DEF，DE交AC于G，连接AE和AD.有下列结论：①AC∥DF；②AD∥BE，AD=BE；③∠B=∠DEF；④ED⊥AC.其中正确的结论有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
9. 经过点M（4，－2）与点N（x，y）的直线平行于x轴，且点N到y轴的距离等于5，由点N的坐标是（）

A、（5，2）或（－5，－2） B、（5，－2）或（－5，－2） C、（5，－2）或（－5，2） D、（5，－2）或（－2，－2）

查看试题解析
10. 如图，下列各三角形中的三个数之间均具有相同的规律，根据此规律，最后一个三角形中y与n之间的关系是（）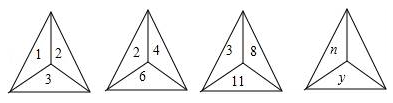

A、y=2n+1 B、y=2ⁿ+n C、y=2ⁿ⁺¹+n D、y=2ⁿ+n+1

查看试题解析

二、填空题

11. 16的算术平方根是.－27的立方根是. $\sqrt{81}$ 的平方根.

查看试题解析
12. 为了了解某校学生进行课外阅读的情况，从全校2200名学生中随机抽取了100名学生，对他们平均每天进行课外阅读的时长进行统计，样本容量是.

查看试题解析
13. 若 ${\begin{array}{l} x = 2 \\ y = - 3 \end{array}$ 和 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ 都是关于x，y的方程y=kx+b的解，则k+2b的值是.

查看试题解析

14. 某公园划船项目收费标准如下：

船型	两人船（限两人）	四人船（限四人）	六人船（限六人）	八人船（限八人）
每船租金（元/时）	70	100	130	150

某班18名同学一起去该公园划船，若每人划船的时间均为1.5小时，则租船的总费用最低为元.

查看试题解析

15. 如图，OC平分∠AOB，D是射线OA上一点，DE∥OB交OC于点E，若∠1=40°，则∠ODE的度数为.

查看试题解析
16. 在平面直角坐标系中，对于任意三点A，B，C的“矩面积”，给出如下定义：“水平底”a：任意两点横坐标差的最大值，“铅垂高”h：任意两点纵坐标差的最大值，则“矩面积”S=ah.例如，三点坐标分别为A（0，3），B（-3，4），C（1，-2），则“水平底”a=4，“铅垂高”h=6，“矩面积”S=ah=24.若D（2，2），E（-2，-1），F（3，m）三点的“矩面积”为20，则m的值为.

查看试题解析

三、解答题

17. 计算与求解：

(1)、 $\sqrt[3]{- 8} - \sqrt{5} - | \sqrt{5} - 3 |$

(2)、解方程组： ${\begin{array}{l} 3 (x- 1) = y + 5 \\ 5 (y- 1) = 3 (x + 5) \end{array}$

查看试题解析
18. 解不等式（组）：

(1)、 $1 - \frac{x - 3}{6} > \frac{x}{3}$

(2)、解不等式组，把解集在数轴上表示出来.并写出它的所有整数解.
${\begin{array}{l} 1 + x > - 2 \\ \frac{2 x - 1}{3} \leq 1 \end{array}$

查看试题解析
19. 根据直尺和三角尺的实物摆放图，解决下列问题.

(1)、如图1，是我们学过的用直尺和三角尺画平行线的方法的示意图，画图的原理是；

(2)、如图2，图中互余的角有，若要使直尺的边缘DE与三角尺的AB边平行，则应满足（填角相等）；

(3)、如图3，若BC∥GH，试判断AC和FG的位置关系，并证明.

查看试题解析

20. 市实验中学学生会准备调查七年级学生参加“球类”“书画类”“棋牌类：”“器乐类”四类校本课程的人数.

(1)、确定调查方式时，甲同学说：“我到七年级（1）班去调查全体同学”；乙同学说：“放学时，我到校门口随机调查部分同学”；丙同学说：“我到七年级每个班随机调查一定数量的同学”.这三位同学的调查方式中，最合理的是（填“甲”“乙”或“丙”）同学的调查方式.

(2)、他们采用了最为合理的调查方法收集数据，并绘制了如图所示的统计表和扇形统计图，请你根据图表提供的信息解答下列问题：

①a= ， b=；

②在扇形统计图中，器乐类所对应的圆心角的度数是；

③若该校七年级有学生660人，请你估计大约有多少学生参加球类校本课程?

类别	频数（人数）	百分比
球类	25
书画类	20	20%
棋牌类	15	b
器乐类
合计	a	100%

查看试题解析

21. 如图，在三角形ABC中，过A作AD⊥BC，垂足为D，E为AB上一点，过点E作EF⊥BC，垂足为点F，过点D作DG∥AB交AC于点G.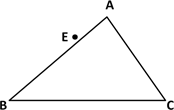

(1)、依题意补全图形；

(2)、求证：∠BEF＝∠ADG

查看试题解析
22. 阅读材料并把解答过程补充完整.
问题：在关于x，y的二元一次方程组 ${\begin{array}{l} x - y = 2 \\ x + y = a \end{array}$ 中，x>1，y<0，求a的取值范围.

分析：在关于x，y的二元一次方程组中，利用参数a的代数式表示x，y，然后根据x>1，y<0列出关于参数a的不等式组即可求得a的取值范围.

解：由 ${\begin{array}{l} x - y = 2 \\ x + y = a \end{array}$ ，解得 ${\begin{array}{l} x = \frac{a + 2}{2} \\ y = \frac{a - 2}{2} \end{array}$ ，又因为x>1，y<0，所以 ${\begin{array}{l} \frac{a + 2}{2} > 1 \\ \frac{a - 2}{2} < 0 \end{array}$ ，解得__▲_.

请你按照上述方法，完成下列问题：

已知x-y=4，x>3，y<1，求x+y的取值范围.

查看试题解析
23. 某商场销售A、B两种品牌的教学设备，这两种教学设备的进价和售价如下表所示：

教学设备

A

B

进价（万元/套）

3

2.4

售价（万元/套）

3.3

2.8

该商场计划购进两种教学设备若干套，共需132万元，全部销售后可获毛利润18万元.

(1)、该商场计划购进A、B两种品牌的教学设备各多少套？

(2)、通过市场调查，该商场决定在原计划的基础上，减少A种设备的购进数量，增加B种设备的购进数量，已知B种设备增加的数量是A种设备减少数量的1.5倍.若用于购进这两种教学设备的总资金不超过138万元，则A种设备购进数量最多减少多少套？

查看试题解析
24. 在平面直角坐标系中，点A，B，C的坐标分别为A（a，3），B（b，6），C（m+6，1），且a，b满足 ${\begin{array}{l} 2 a + 3 b = 5 m + 12 \\ 3 a + b = 4 m + 4 \end{array}$

(1)、请用含m的式子表示A，B两点的坐标；

(2)、如图，点A在第二象限，点B在第一象限，连接A、B、C、O四点；
①若点B到y轴的距离不小于点A到y轴距离的2倍，试求m的取值范围；

②若三角形AOC的面积等于三角形ABC面积的 $\frac{2}{3}$ ，求实数m的值.

查看试题解析

教学设备	A	B
进价（万元/套）	3	2.4
售价（万元/套）	3.3	2.8