湖北省黄石市下陆区2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2020-07-15 类型：期末考试

进入出卷网下载

一、选择题

1. 9的算术平方根是（）

A、 ﹣3 B、±3 C、3 D、 $\sqrt{3}$

查看试题解析
2. 点P（m﹣1，m+3）在直角坐标系的y轴上，则P点坐标为（　　）

A、（﹣4，0） B、（0，﹣4） C、（4，0） D、（0，4）

查看试题解析
3. 已知 $x > y$ ,则下列不等式成立的是（）

A、 $x - 1 < y - 1$ B、 $3 x < 3 y$ C、-x＜-y D、 $\frac{x}{2} < \frac{y}{2}$

查看试题解析
4. 如图，将长方形纸条 $A B C D$ 沿 $E F$ 叠后， $E D$ 与 $B F$ 交于 $G$ 点，若 $∠ E F C = 130^{°}$ ，则 $∠ A E D$ 的度数为（）

A、 $55^{\circ}$ B、 $70^{\circ}$ C、 $75^{\circ}$ D、 $80^{\circ}$

查看试题解析
5. 如图，将△ABC沿BC方向平移2cm得到△DEF，若△ABC的周长为16cm，则四辺形ABFD的周长为（）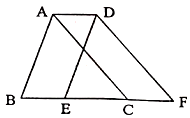

A、16cm B、18cm C、20cm D、22cm

查看试题解析
6. 若方程组 ${\begin{array}{l} \begin{matrix} 3 x + 2 y = a + 4 \\ 2 x + 3 y = a \end{matrix} \end{array}$ 的解x与y的和为2，则a的值为(　　)

A、7 B、3 C、0 D、 $- 3$

查看试题解析
7. 若一元一次不等式组 ${\begin{array}{l} x \leq 7 \\ x - 1 \geq m \end{array}$ 有解，则 $m$ 的取值范围是（）

A、 $m > 6$ B、 $m \geq 6$ C、 $m < 7$ D、 $m \leq 6$

查看试题解析
8. 某种衬衫的进价为400元，出售时标价为550元，由于换季，商店准备打折销售，但要保持利润不低于10%，那么至多打（　　）

A、6折 B、7折 C、8折 D、9折

查看试题解析
9. 如图，已知 $A B / / C D ， ∠ E B F = 2 ∠ A B E ，$ $∠ E D F = 2 ∠ C D E$ ，则 $∠ E$ 与 $∠ F$ 之间满足的数量关系是（）

A、 $∠ E = ∠ F$ B、 $∠ E + ∠ F = 180^{\circ}$ C、 $3 ∠ E + ∠ F = 360^{\circ}$ D、 $2 ∠ E - ∠ F = 90^{\circ}$

查看试题解析
10. 一个质点在第一象限及 $x$ 轴、 $y$ 轴上运动，在第一秒钟，它从原点运动到 $(0 ， 1)$ ，然后接着按图中箭头所示方向运动，且每秒移动一个单位，那么第 $80$ 秒时质点所在位置的坐标是（）

A、 $(0 ， 9)$ B、 $(9 ， 0)$ C、 $(0 ， 8)$ D、 $(8 ， 0)$

查看试题解析

二、填空题

11. 要使 $\sqrt{x - 4}$ 有意义，则x的取值范围是

查看试题解析
12. 为了调查滨湖区八年级学生期末考试数学试卷答题情况，从全区的数学试卷中随机抽取了10本没拆封的试卷作为样本，每本含试卷30份，这次抽样调查的样本容量是．

查看试题解析
13. 若a是 $\sqrt{5}$ 的整数部分，b是它的小数部分，则a+b= .

查看试题解析
14. 已知点 $A (1, 2)$ ， $A C / / x$ 轴， $A C = 5$ ，则点C的坐标是 .

查看试题解析
15. 小明在拼图时，发现 $8$ 个一样大小的长方形，恰好可以拼成一个大的长方形如图(1)；小红看见了，说：“我也来试试.”结果小红七拼八凑，拼成了如图(2)那样的正方形，中间还留下了一个洞，恰好是边长为 $5 m m$ 的小正方形，则每个小长方形的面积为 $m m^{2}$ .

查看试题解析
16. 若不等式组 ${\begin{cases} x < 1 \\ x > m - 2 \end{cases}$ 恰有两个整数解，则m的取值范围是．

查看试题解析

三、解答题

17. 计算

(1)、 $\sqrt{4} + | - 2 | + \sqrt[3]{- 27} + {(- 1)}^{2016}$

(2)、 $\sqrt[3]{- 8} + | \sqrt{3} - 2 | + \sqrt{{(- 3)}^{2}} - (- \sqrt{3})$

查看试题解析
18. 用适当的方法解方程组

(1)、 ${\begin{array}{l} x = 3 - y \\ 3 x + 2 y = 2 \end{array}$

(2)、 ${\begin{array}{l} 3 x - 5 y = 3 \\ \frac{x}{2} - \frac{y}{3} = 1 \end{array}$

查看试题解析
19. 解不等式组 ${\begin{array}{l} 2 x + 1 \geq 1 \\ \frac{1 + 2 x}{3} > x - 1 \end{array}$ ，并把不等式组的解集在数轴上表示出来.

查看试题解析
20. 已知：如图， $A D / / B E$ ， $∠ 1 = ∠ 2$ ，求证： $∠ A = ∠ E$ .

查看试题解析
21. 已知关于 $x 、 y$ 的方程组 ${\begin{array}{l} x + y = - m - 7 \\ x - y = 3 m + 1 \end{array}$ 的解满足 $x \leq 0, y < 0$ .

(1)、求 $m$ 的取值范围:

(2)、在 $m$ 的取值范围内，当 $m$ 为何整数时，不等式 $2 m x + x < 2 m + 1$ 的解为 $x > 1$ ?

查看试题解析
22. 某校为了了解七年级学生体育测试情况，以七年级（1）班学生的体育测试成绩为样本，按A、B、C、D四个等级进行统计，并将统计结果绘制如下的统计图，请你结合图中所给的信息解答下列问题：

（说明：A级：90分~100分；B级：75分~89分；C级：60分~74分；D级：60分以下）

(1)、请把条形统计图补充完整；

(2)、扇形统计图中D级所在的扇形的圆心角度数是；

(3)、若该校七年级有600名学生，请用样本估计体育测试中A级学生人数约为多少人？

查看试题解析
23. 为保护环境，我市公交公司计划购买A型和B型两种环保节能公交车共10辆．若购买A型公交车1辆，B型公交车2辆，共需400万元；若购买A型公交车2辆，B型公交车1辆，共需350万元．

(1)、求购买A型和B型公交车每辆各需多少万元？

(2)、预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次．若该公司购买A型和B型公交车的总费用不超过1200万元，且确保这10辆公交车在该线路的年均载客总和不少于680万人次，则该公司有哪几种购车方案？

(3)、在（2）的条件下，哪种购车方案总费用最少？最少总费用是多少万元？

查看试题解析
24. 如图，在下面直角坐标系中，已知 $A (- 4 ， - 4) ， B (- 8 ， 0)$

(1)、求 $Δ A B O$ 的面积

(2)、若以点 $A 、 B 、 O$ 为顶点画平行四边形，则请你“利用平移的知识”直接写出符合条件的所有的平行四边形的第四个顶点 $C$ 的坐标

(3)、是否存在 $x$ 轴上的点 $M (x ， 0)$ ，使 $Δ A B M$ 的面积是 $Δ A B O$ 的面积的 $2$ 倍，若存在，求出点 $M$ 的坐标；若不存在，请说明理由.

查看试题解析
25. 如图1， $C$ 点是第二象限内一点， $C B ⊥ y$ 轴于 $B$ ，且 $B (0 ， b)$ 是 $y$ 轴正半轴上一点， $A (a ， 0)$ 是x轴负半 $x$ 轴上一点，且 $| a + 2 | + {(b - 3)}^{2} = 0 ， S_{四边形 A O B C} = 9$ .

(1)、 $A$ （）， $B$ （）

(2)、如图2，设 $D$ 为线段 $O B$ 上一动点，当 $A D ⊥ A C$ 时， $∠ O D A$ 的角平分线与 $∠ C A E$ 的角平分线的反向延长线交于点 $P$ ，求 $∠ A P D$ 的度数： (注：三角形三个内角的和为 $180^{\circ}$ )

(3)、如图3，当 $D$ 点在线段 $O B$ 上运动时，作 $D M ⊥ A D$ 交 $C B$ 于 $M ， ∠ B M D ， ∠ D A O$ 的平分线交于 $N$ ，当 $D$ 点在运动的过程中， $∠ N$ 的大小是否变化?若不变，求出其值；若变化，请说明理由.

查看试题解析