湖北省丹江口市2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2020-07-15 类型:期末考试
一、选择题
-
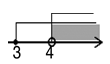
1. 9的算术平方根是( )A、±3 B、3 C、-3 D、62. 不等式组 的解集在数轴上表示为( )A、
 B、
B、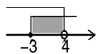 C、
C、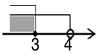 D、
D、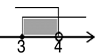 3. 下列调查活动中适合用全面调查的是( )A、“最强大脑”节目的收视率 B、调查乘坐飞机的旅客是否带了违禁物品 C、某种品牌节能灯的使用寿命 D、了解我省中学生课外阅读的情况4. 第二象限内一点 P 到 x 轴的距离等于 2 ,到y轴的距离等于 3 ,则点 P 的坐标为( )A、 B、 C、 D、5. 下列各组数是二元一次方程组 的解的是( )A、 B、 C、 D、6. 已知 ,则下列不等式一定成立的是( )A、 B、 C、 D、7. 如图,在 中, ,高 , 交于点 则 是( )
3. 下列调查活动中适合用全面调查的是( )A、“最强大脑”节目的收视率 B、调查乘坐飞机的旅客是否带了违禁物品 C、某种品牌节能灯的使用寿命 D、了解我省中学生课外阅读的情况4. 第二象限内一点 P 到 x 轴的距离等于 2 ,到y轴的距离等于 3 ,则点 P 的坐标为( )A、 B、 C、 D、5. 下列各组数是二元一次方程组 的解的是( )A、 B、 C、 D、6. 已知 ,则下列不等式一定成立的是( )A、 B、 C、 D、7. 如图,在 中, ,高 , 交于点 则 是( )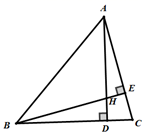 A、 B、 C、 D、8. 从甲地到乙地有一段上坡与一段平路,如果保持上坡每小时走 ,平路每小时走 .下坡每小时走 ,那么从甲地到乙地需 ,从乙地到甲地需 .设从甲地到乙地的上坡路程长 ,平路路程长为 ,依题意列方程组正确的是( )A、 B、 C、 D、9. 如图,在 中, 是边 上点, ,点 是 的中点。连接 , 交于 ,已知 ,则 ( )
A、 B、 C、 D、8. 从甲地到乙地有一段上坡与一段平路,如果保持上坡每小时走 ,平路每小时走 .下坡每小时走 ,那么从甲地到乙地需 ,从乙地到甲地需 .设从甲地到乙地的上坡路程长 ,平路路程长为 ,依题意列方程组正确的是( )A、 B、 C、 D、9. 如图,在 中, 是边 上点, ,点 是 的中点。连接 , 交于 ,已知 ,则 ( ) A、 B、 C、 D、10. 对于有理数 、 ,定义 的含义为:当 时, ,例如: .已知 , ,且 和 为两个连续正整数,则 的立方根为( )A、 B、 C、 D、
A、 B、 C、 D、10. 对于有理数 、 ,定义 的含义为:当 时, ,例如: .已知 , ,且 和 为两个连续正整数,则 的立方根为( )A、 B、 C、 D、二、填空题
-
11. 的绝对值是 .12. 若点 在 轴上.则 点的坐标为.13. 已如等腰 的两边长 , 满足 ,则第三边长 的值为14. 若关于 的不等式组 只有4个正整数解,则 的取值范围为.
三、解答题
-
15. 计算:16. 解方程组、不等式:(1)、解方程组 ;(2)、解不等式 .17. 七年级数学研究学习小组在某十字路口随机调查部分市民对“社会主义核心价值观”的了解情况,统计结果后绘制了如图的两副不完整的统计图,请结合图中相关数据回答下列问题:
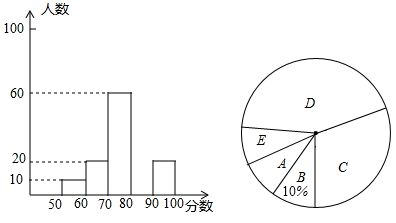
得分
(1)、本次调查的总人数为人, 在扇形统计图中“心所在扇形的圆心角的度数为:(2)、补全频数分布图:(3)、若在这周里,该路口共有 人通过,请估计得分超过 的约有多少人?18. 若点 的横纵坐标同号,且点P到两坐标轴的距离相等,求 的平方根,19. 如图,点F是△ABC的边BC延长线上一点.DF⊥AB,∠A=30°,∠F=40°,求∠ACF的度数.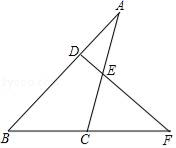 20. 某工前年有员工 人,去年经过结构改革减员 人,全年利润增加 万元,人均创利至少增加 元,前年全年利润至少是多少?21. 已知,以关于 , 的二元次方程组 的解 为坐标的点在第二象限,求 取值范围.22.
20. 某工前年有员工 人,去年经过结构改革减员 人,全年利润增加 万元,人均创利至少增加 元,前年全年利润至少是多少?21. 已知,以关于 , 的二元次方程组 的解 为坐标的点在第二象限,求 取值范围.22.如图,△ABC中,AD⊥BC于点D,BE平分∠ABC,若∠ABC=64°,∠AEB=70°.
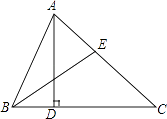 (1)、求∠CAD的度数;(2)、若点F为线段BC上的任意一点,当△EFC为直角三角形时,求∠BEF的度数.23. 某小区准备新建 60 个停车位,以解决小区停车难的问题。已知新建 个地上停车位和 个地下停车位共需 1.7 万元:新建 4 个地上停车位和 2 个地下停车位共需 1.4 万元。(1)、该小区新建 1 个地上停车位和 1个地下停车位各需多少万元?(2)、若该小区新建车位的投资金额超过14 万元而不超过 15万元,问共有几种建造方案?(3)、对(2)中的几种建造方案中,哪种方案的投资最少?并求出最少投资金额.24. 如图1, ,点 , 分别在射线 , 上移动, 是 的平分线, 的反向延长线与 的平分线相交于点 .
(1)、求∠CAD的度数;(2)、若点F为线段BC上的任意一点,当△EFC为直角三角形时,求∠BEF的度数.23. 某小区准备新建 60 个停车位,以解决小区停车难的问题。已知新建 个地上停车位和 个地下停车位共需 1.7 万元:新建 4 个地上停车位和 2 个地下停车位共需 1.4 万元。(1)、该小区新建 1 个地上停车位和 1个地下停车位各需多少万元?(2)、若该小区新建车位的投资金额超过14 万元而不超过 15万元,问共有几种建造方案?(3)、对(2)中的几种建造方案中,哪种方案的投资最少?并求出最少投资金额.24. 如图1, ,点 , 分别在射线 , 上移动, 是 的平分线, 的反向延长线与 的平分线相交于点 .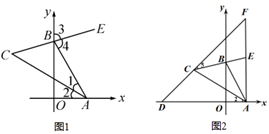 (1)、试问 的大小是否发生变化,如果保持不变,请求出 的度数,如果随点 , 的移动发生变化,请求出变化的范围(2)、如图2,点 在 轴负半轴上,过点 作 轴交 与点 ,交 的延长线于点 ,若 试问 与 有何关系?请证明你的结论.
(1)、试问 的大小是否发生变化,如果保持不变,请求出 的度数,如果随点 , 的移动发生变化,请求出变化的范围(2)、如图2,点 在 轴负半轴上,过点 作 轴交 与点 ,交 的延长线于点 ,若 试问 与 有何关系?请证明你的结论.