湖北省安陆市2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2020-07-15 类型:期末考试
一、选择题
-
1. 在﹣3, ,0,1四个数中,是无理数的是( )A、﹣3 B、 C、0 D、12. 面积为 的正方形的边长是( )A、 开平方的结果 B、 的平方根 C、 的立方根 D、 的算术平方根3. 要反映台州市某一周每天的最高气温的变化趋势,宜采用( )A、条形统计图 B、扇形统计图 C、折线统计图 D、频数分布统计图4. 如图,直线a∥b,直线l与a,b分别交于点A,B,过点A作AC⊥b于点C,若∠1=50°,则∠2的度数为( )
 A、130° B、50° C、40° D、25°5. 如果点P(2x+6,x-4)在平面直角坐标系的第四象限内,那么x的取值范围在数轴上可表示为A、
A、130° B、50° C、40° D、25°5. 如果点P(2x+6,x-4)在平面直角坐标系的第四象限内,那么x的取值范围在数轴上可表示为A、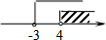 B、
B、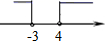 C、
C、 D、
D、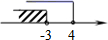 6. 已知关于x、y的二元一次方程组 的解是 ,则 的值是( )A、1 B、2 C、﹣1 D、07. 如图,若△DEF是由 平移后得到的,已知点 之间的距离为1, 则 ( )
6. 已知关于x、y的二元一次方程组 的解是 ,则 的值是( )A、1 B、2 C、﹣1 D、07. 如图,若△DEF是由 平移后得到的,已知点 之间的距离为1, 则 ( )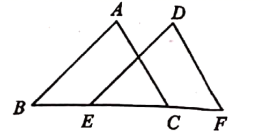 A、1 B、2 C、3 D、不确定8. 已知点 ,当 两点间的距离最短时, 的值为( )A、 B、 C、 D、9. 若不等式组 无解,则 的取值范围为( )A、 B、 C、 D、10. 如表,已知表格中竖直、水平、对角线上的三个数的和都相等,则 ( )
A、1 B、2 C、3 D、不确定8. 已知点 ,当 两点间的距离最短时, 的值为( )A、 B、 C、 D、9. 若不等式组 无解,则 的取值范围为( )A、 B、 C、 D、10. 如表,已知表格中竖直、水平、对角线上的三个数的和都相等,则 ( )m
-3
4
3
1
n
A、 B、 C、 D、11. 如果关于 的不等式 的解集为 ,写出一个满足条件的 的值:.12. 结合下图,用符号语言表达定理“同旁内角互补,两直线平行”的推理形式:∵ ,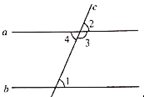 13. 一般地,如果 ,则称 为 的四次方根,一个正数 的四次方根有两个.它们互为相反数,记为 ,若 ,则 .14. 《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”译文大致是:“用一根绳子去量一根木条,绳子剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?”如果设木条长x尺,绳子长y尺,可列方程组为;15. 已知三元一次方程组 ,则 .16. 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“ ”方向排列,如 ….根据这个规律探索可得,第 个点的坐标为.
13. 一般地,如果 ,则称 为 的四次方根,一个正数 的四次方根有两个.它们互为相反数,记为 ,若 ,则 .14. 《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”译文大致是:“用一根绳子去量一根木条,绳子剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?”如果设木条长x尺,绳子长y尺,可列方程组为;15. 已知三元一次方程组 ,则 .16. 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“ ”方向排列,如 ….根据这个规律探索可得,第 个点的坐标为.
二、解答题
-
17. 解不等式,并把它的解集在数轴上表示出来.
 18. 数学课上老师要求学生解方程组:
18. 数学课上老师要求学生解方程组:同学甲的做法是:
由①,得a=- + b.③
把③代入②,得3b=11-3(- + b),解得b= .
把b= 代入③,解得a=2.
所以原方程组的解是
老师看了同学甲的做法说:“做法正确,但是方法复杂,要是能根据题目特点,采用更加灵活简便的方法解此题就更好了.”请你根据老师提供的思路解此方程组.
19. 已知关于 , 的二元一次方程组 的解满足 ,其中 是非负整数,求 的值.20. 争创全国文明城市,从我做起,某学校在七年级开设了文明礼仪校本课程,为了解学生的学习情况,学校随机抽取30名学生进行测试,成绩如下(单位:分):78 83 86 86 90 94 97 92 89 86 84 81 81 84 86 88 92 89 86 83 81 81 85 86 89 93 93 89 85 93,整理上面的数据得到频数分布表和频数分布直方图:成绩(分)
频数
5
11
2
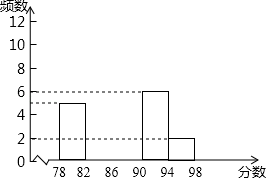
回答下列问题:
(1)、以上30个数据中,中位数是;频数分布表中a=;b=;(2)、补全频数分布直方图;(3)、若成绩不低于86分为优秀,估计该校七年级300名学生中,达到优秀等级的人数.21. 平行四边形可以看成是线段平移得到的图形,如图将线段 沿 的方向平移 个单位至 处,就可以得到平行四边形 ,或者将线段 沿 的方向平移 个单位至 处,也可以得到平行四边形 .如图2在 的方格纸(每个小正方形的边长都为 )中,点 都在格点上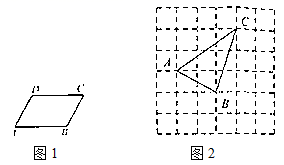 (1)、按要求画图:在图中找出格点 ,使以 为顶点的四边形是平行四边形,并画出平行四边形;(2)、在(1)中所画出的平行四边形的面积为.22. 如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的相伴方程.(1)、在方程 ①, ②, ③中,写出是不等式组 的相伴方程的序号.(2)、写出不等式组 的一个相伴方程,使得它的根是整数:.(3)、若方程 都是关于 的不等式组 的相伴方程,求 的取值范围.23. 某公司组织退休职工组团前往某景点游览参观,参加人员共70人.旅游景点规定:①门票每人60元,无优惠;②上山游览必须乘坐景点安排的观光车游览,观光车有小型车和中型车两类,分别可供4名和11名乘客乘坐;且小型车每辆收费60元,中型车每人收费10元.若70人正好坐满每辆车且参观游览的总费用不超过5000元,问景点安排的小型车和中型车各多少辆?24. 探究题:已知:如图, , .求证: .
(1)、按要求画图:在图中找出格点 ,使以 为顶点的四边形是平行四边形,并画出平行四边形;(2)、在(1)中所画出的平行四边形的面积为.22. 如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的相伴方程.(1)、在方程 ①, ②, ③中,写出是不等式组 的相伴方程的序号.(2)、写出不等式组 的一个相伴方程,使得它的根是整数:.(3)、若方程 都是关于 的不等式组 的相伴方程,求 的取值范围.23. 某公司组织退休职工组团前往某景点游览参观,参加人员共70人.旅游景点规定:①门票每人60元,无优惠;②上山游览必须乘坐景点安排的观光车游览,观光车有小型车和中型车两类,分别可供4名和11名乘客乘坐;且小型车每辆收费60元,中型车每人收费10元.若70人正好坐满每辆车且参观游览的总费用不超过5000元,问景点安排的小型车和中型车各多少辆?24. 探究题:已知:如图, , .求证: .
老师要求学生在完成这道教材上的题目证明后,尝试对图形进行变形,继续做拓展探究,看看有什么新发现?
(1)、小颖首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小颖用到的平行线性质可能是.(2)、接下来,小颖用《几何画板》对图形进行了变式,她先画了两条平行线 ,然后在平行线间画了一点 ,连接 后,用鼠标拖动点 ,分别得到了图 ,小颖发现图 正是上面题目的原型,于是她由上题的结论猜想到图 和 图中的与 之间也可能存在着某种数量关系.于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.请你在小颖操作探究的基础上,继续完成下面的问题:
(ⅰ)猜想图 中 与 之间的数量关系并加以证明;
(ⅱ)补全图 ,直接写出 与 之间的数量关系:.