河南省南阳市唐河县2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2020-07-15 类型:期末考试
一、选择题
-
1. 若x>y,则下列式子中错误的是( )A、 B、 C、 D、2. 在这些汽车标识中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图, 经过平移得到 ,其中点A的对应点是点D,则下列结论不一定正确的是( )
3. 如图, 经过平移得到 ,其中点A的对应点是点D,则下列结论不一定正确的是( ) A、 B、 C、 D、4. 如图所示,一个正方形水池的四周恰好被4个正n边形地板砖铺满,则 等于( )
A、 B、 C、 D、4. 如图所示,一个正方形水池的四周恰好被4个正n边形地板砖铺满,则 等于( )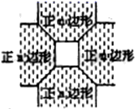 A、6 B、8 C、9 D、105. 如图,香港特别行政区标志紫荆花图案绕中心旋转n°后能与原来的图案互相重合,则n的最小值为( )
A、6 B、8 C、9 D、105. 如图,香港特别行政区标志紫荆花图案绕中心旋转n°后能与原来的图案互相重合,则n的最小值为( ) A、45 B、60 C、72 D、1446. 若关于x的方程x﹣2+3k= 的解是正数,则k的取值范围是( )
A、45 B、60 C、72 D、1446. 若关于x的方程x﹣2+3k= 的解是正数,则k的取值范围是( )
A、k> B、k≥ C、k< D、k≤7. 把一些书分给几名同学,若______;若每人分11本,则有剩余.依题意,设有 名同学,可列不等式 ,则横线的信息可以是( )A、每人分7本,则剩余8本 B、每人分7本,则可多分8个人 C、每人分8本,则剩余7本 D、其中一个人分7本,则其他同学每人可分8本8. 下列各图形分别绕某个点旋转 后不能与自身重合的是( ).A、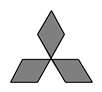 B、
B、 C、
C、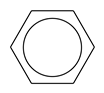 D、
D、 9. 《九章算术》中记载:“今有共买羊,人出五,不足四十五人出七,不足三,问人数、羊价各几何?”其大意是:今有人合伙买羊,若每人出 钱,还差 钱;若每人出 钱,还差 钱,问合伙人数、羊价各是多少?设合伙人数为 人,羊价为 钱,根据题意,可列方程组为( ).A、 B、 C、 D、10. 如图所示,小明从 点出发,沿直线前进8米后左转 ,再沿直线前进8米,又左转 ,照这样走下去,他第一次回到出发点 时,一共走了( )米.
9. 《九章算术》中记载:“今有共买羊,人出五,不足四十五人出七,不足三,问人数、羊价各几何?”其大意是:今有人合伙买羊,若每人出 钱,还差 钱;若每人出 钱,还差 钱,问合伙人数、羊价各是多少?设合伙人数为 人,羊价为 钱,根据题意,可列方程组为( ).A、 B、 C、 D、10. 如图所示,小明从 点出发,沿直线前进8米后左转 ,再沿直线前进8米,又左转 ,照这样走下去,他第一次回到出发点 时,一共走了( )米. A、70 B、72 C、74 D、76
A、70 B、72 C、74 D、76二、填空题
-
11. 已知三角形的三边长分别为2,x﹣1,3,则三角形周长y的取值范围是 .
12. 如图所示, . 13. 若不等式组 的解集是-1<x<1,则(a+b)2019= .14. 一组“数值转换机”按下面的程序计算,如果输入的数是36,则输出的结果为106,要使输出的结果为127,则输入的最小正整数是.
13. 若不等式组 的解集是-1<x<1,则(a+b)2019= .14. 一组“数值转换机”按下面的程序计算,如果输入的数是36,则输出的结果为106,要使输出的结果为127,则输入的最小正整数是. 15. 如图,在直角三角尺 与 中, , , .三角尺 不动,将三角尺 的 边与 边重合,然后绕点 按顺时针方向任意转动一个角度.当 ( )等于多少度时,这两块三角尺各有一条边互相垂直,写出 所有可能的值是.
15. 如图,在直角三角尺 与 中, , , .三角尺 不动,将三角尺 的 边与 边重合,然后绕点 按顺时针方向任意转动一个角度.当 ( )等于多少度时,这两块三角尺各有一条边互相垂直,写出 所有可能的值是.
三、解答题
-
16. 解下列方程(组):(1)、(2)、17. 解不等式组 并将解集在数轴上表示出来.18.(1)、如图是一个4×4的正方形网格,每个小正方形的边长均为1.请在网格中以左上角的三角形为基本图形,通过平移、对称或旋转,设计两个精美图案,使其满足:①既是轴对称图形,又能以点 为旋转中心旋转而得到;②所作图案用阴影标识,且阴影部分面积为4.
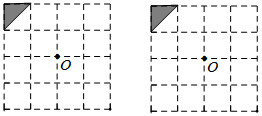 (2)、如图, 的三个顶点和点 都在正方形网格的格点上,每个小正方形的边长都为1.
(2)、如图, 的三个顶点和点 都在正方形网格的格点上,每个小正方形的边长都为1.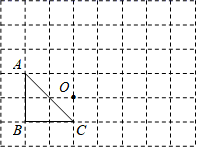
①将 先向右平移4个单位,再向上平移2个单位得到 ,请画出 ;
②请画出 ,使 和 关于点 成中心对称;
19. 某公交公司决定更换节能环保的新型公交车 购买的数量和所需费用如下表所示:A型数量 辆
B型数量 辆
所需费用 万元
3
1
450
2
3
650
(1)、求A型和B型公交车的单价;(2)、该公司计划购买A型和B型两种公交车共10辆,已知每辆A型公交车年均载客量为60万人次,每辆B型公交车年均载客量为100万人次,若要确保这10辆公交车年均载客量总和不少于670万人次,则A型公交车最多可以购买多少辆?20. 如图,观察每个正多边形中 的变化情况,解答下列问题: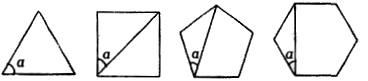 ……(1)、将下面的表格补充完整:
……(1)、将下面的表格补充完整:正多边形的边数
3
4
5
6
……
的度数
……
(2)、根据规律,是否存在一个正 边形,使其中的 ?若存在,写出 的值;若不存在,请说明理由.(3)、根据规律,是否存在一个正 边形,使其中的 ?若存在,写出 的值;若不存在,请说明理由.21. 如图,四边形ABCD是正方形,△ADF按顺时针方向旋转一定角度后得到△ABE,点E落在AD边上,若AF=4.AB=7. (1)、旋转中心为;旋转角度为;(2)、求DE的长度;(3)、指出BE与DF的关系如何?并说明理由.22. 去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.(1)、求饮用水和蔬菜各有多少件?(2)、现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;(3)、在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?23.
(1)、旋转中心为;旋转角度为;(2)、求DE的长度;(3)、指出BE与DF的关系如何?并说明理由.22. 去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.(1)、求饮用水和蔬菜各有多少件?(2)、现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;(3)、在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?23. (1)、思考探究:如图①, 的内角 的平分线与外角 的平分线相交于 点,请探究 与 的关系是.(2)、类比探究:如图②,四边形 中,设 , , ,四边形 的内角 与外角 的平分线相交于点 .求 的度数.(用 , 的代数式表示)(3)、拓展迁移:如图③,将(2)中 改为 ,其它条件不变,请在图③中画出 ,并直接写出 .(用 , 的代数式表示)
(1)、思考探究:如图①, 的内角 的平分线与外角 的平分线相交于 点,请探究 与 的关系是.(2)、类比探究:如图②,四边形 中,设 , , ,四边形 的内角 与外角 的平分线相交于点 .求 的度数.(用 , 的代数式表示)(3)、拓展迁移:如图③,将(2)中 改为 ,其它条件不变,请在图③中画出 ,并直接写出 .(用 , 的代数式表示)