河南省南阳市南召县2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2020-07-15 类型：期末考试

进入出卷网下载

一、选择题

1. 已知x＝－2是方程2x＋m－4＝0的一个根，则m的值是（）

A、8 B、－8 C、0 D、2

查看试题解析
2. 已知 ${\begin{cases} x = 2 \\ y = - 1 \end{cases}$ 是关于x，y的二元一次方程的解，则的值为（）

A、3 B、-3 C、 $\frac{9}{2}$ D、-11

查看试题解析
3. 不等式 $\frac{1}{2} x - 1 > x$ 的解集是（　　）

A、 $x > 1$ B、 $x > - 2$ C、 $x < \frac{1}{2}$ D、 $x < - 2$

查看试题解析
4. 已知三角形的三边长分别为1，2，x，则x的取值范围在数轴上表示为(　　)

A、 B、 C、 D、

查看试题解析
5. 一个正多边形的内角和为540°，则这个正多边形的每一个外角等于（）

A、108° B、90° C、72° D、60°

查看试题解析
6. 关于x的不等式x-b>0恰有两个负整数解，则b的取值范围是

A、 $- 3 \leq b < - 2$ B、 $- 3 < b \leq - 2$ C、 $- 3 \leq b \leq - 2$ D、 $-3<b<-2$

查看试题解析
7. 如图，ABCD四点在同一条直线上，△ACE≌△BDF，则下列结论正确的是（　　）

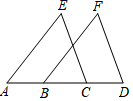A、△ACE和△BDF成轴对称 B、△ACE经过旋转可以和△BDF重合 C、△ACE和△BDF成中心对称 D、△ACE经过平移可以和△BDF重合

查看试题解析
8. 如图，将周长为4的△ABC沿BC方向向右平移1个单位得到△DEF，则四边形ABFD的周长为（）

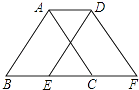A、5 B、6 C、7 D、8

查看试题解析
9. 如图，在6×4的方格纸中，格点三角形甲经过旋转后得到格点三角形乙，则其旋转中心是（）

A、点M B、格点N C、格点P D、格点Q

查看试题解析
10. 如图，在△ABC中，∠CAB＝75°，在同一平面内，将△ABC绕点A逆时针旋转到△AB′C′的位置，使得CC′∥AB，则∠CAC′为（）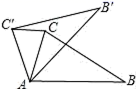

A、30° B、35° C、40° D、50°

查看试题解析

二、填空题

11. 若3x+2与﹣2x+1互为相反数，则x﹣2的值是．

查看试题解析
12. 写出不等式组 ${\begin{array}{l} x \geq - 1 ， \\ x < 1 \end{array}$ 的整数解为.

查看试题解析
13. 甲、乙、丙三种商品，若购买甲3件、乙2件、丙1件，共需130元钱，购甲1件、乙2件、丙3件共需210元钱，那么购甲、乙、丙三种商品各一件共需元.

查看试题解析
14. 如图，将三角板 $A B C$ 沿 $B C$ 方向平移，得到三角形 $A' C C'$ .已知 $∠ B = 30 °$ ， $∠ A C B = 90 °$ ，则 $∠ B A A'$ 的度数为.

查看试题解析
15. 如图，在△ABC中， $B C = 6 c m$ ，将△ABC以每秒2cm的速度沿 $B C$ 所在直线向右平移，所得图形对应为△DEF，设平移时间为t秒，若要使 $A D = 2 C E$ 成立，则 $t$ 的值为秒.

查看试题解析

三、解答题

16. 解方程组： ${\begin{cases} 3 x + 2 y ＝ 8 \\ 2 x - y ＝ 3 \end{cases}$ .

查看试题解析
17. 解不等式组： ${\begin{array}{l} 2 x > 3 x - 2 ① \\ \frac{2 x - 1}{3} \geq \frac{1}{2} x - \frac{2}{3} ② . \end{array}$

查看试题解析
18. 已知等式y=ax²+bx+1.当x=-1时，y=4；当x=2时，y=25；则当x=-3时，求y的值.

查看试题解析
19. 如图，在2×2的正方形格纸中，△ABC是以格点为顶点的三角形也称为格点三角形，请你在该正方形格纸中找出与△ABC成轴对称的格点三角形（用阴影描出3个即可）.

查看试题解析
20. 如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（三角形顶点是网格线的交点）和△A₁B₁C₁ ，且△ABC与△A₁B₁C₁ ，成中心对称.

①画出△ABC和△A₁B₁C₁的对称中心 $O$ ；
②将△A₁B₁C₁沿直线 $E D$ 方向向上平移6格，得到△A₂B₂C₂ ，画出△A₂B₂C₂；
③将△A₂B₂C₂绕点C₂顺时针方向旋转90°，得到△A₃B₃C₃ ，画出△A₃B₃C₃.
①连接BB₁、CC₁ ，线段BB₁与线段CC₁的交点为O，点O就是所求的对称中心.
②如图△A₂B₂C₂就是所求的三角形.
③如图△A₃B₃C₃就是所求的三角形.

查看试题解析
21. 为了更好的治理西流湖水质，保护环境，市治污公司决定购买10台污水处理设备．现有A、B两种型号的设备，其中每台的价格，月处理污水量如下表：

A型

B型

价格（万元/台）

a

b

处理污水量（吨／月）

240

200

经调查：购买一台A型设备比购买一台B型设备多2万元，购买2台A型设备比购买3台B型设备少6万元．

(1)、求a，b的值；

(2)、经预算：市治污公司购买污水处理设备的资金不超过105万元，你认为该公司有哪几种购买方案；

(3)、在（2）问的条件下，若每月要求处理西流湖的污水量不低于2040吨，为了节约资金，请你为治污公司设计一种最省钱的购买方案．

查看试题解析
22. 我们知道，可以单独用正三角形、正方形或正六边形铺满地面，如果我们要同时用两种不同的正多边形铺满地面，可以设计出几种不同的组合方案？

(1)、问题解决：
猜想1：是否可以同时用正方形、正八边形两种正多边形组合铺满地面？

验证1并完成填空：在铺地面时，设围绕某一个点有x个正方形和y个正八边形的内角可以拼成一个周角.根据题意：可得方程①：，

整理得②：，

我们可以找到方程的正整数解为③：.

(2)、结论1：铺满地面时，在一个顶点周围围绕着④ ▲ 个正方形和⑤ ▲ 个正八边形的内角可以拼成一个周角，所以同时用正方形和正八边形两种正多边形组合可以铺满地面.
猜想2：是否可以同时用正三角形和正六边形两种正多边形组合铺满地面？若能，请按照上述方法进行验证，并写出所有可能的方案；若不能，请说明理由.

查看试题解析
23. 探究与发现：

(1)、探究一：我们知道，三角形的一个外角等于与它不相邻的两个内角的和.那么，三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢？

已知：如图1，∠FDC与∠ECD分别为△ADC的两个外角，试探究∠A与∠FDC+∠ECD的数量关系.

(2)、探究二：三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系？
已知：如图2，在△ADC中，DP、CP分别平分∠ADC和∠ACD，试探究∠P与∠A的数量关系.

(3)、探究三：若将△ADC改为任意四边形ABCD呢？
已知：如图3，在四边形ABCD中，DP、CP分别平分∠ADC和∠BCD，试利用上述结论探究∠P与∠A+∠B的数量关系.

(4)、探究四：若将上题中的四边形ABCD改为六边形ABCDEF（图4）呢？
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系： ▲ .

查看试题解析

	A型	B型
价格（万元/台）	a	b
处理污水量（吨／月）	240	200