河南省洛阳市2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2020-07-15 类型:期末考试
一、选择题
-
1. 下列各数中最大的数是A、 B、 C、 D、02. 下列说法正确的是( )A、无限小数都是无理数 B、9的立方根是3 C、数轴上的每一个点都对应一个有理数 D、平方根等于本身的数是03. 下列调查,比较适合全面调查方式的是A、乘坐地铁的安检 B、长江流域水污染情况 C、某品牌圆珠笔笔芯的使用寿命 D、端午节期间市场上的粽子质量情况4. 已知点P(0,a)在y轴的负半轴上,则点Q(﹣a2﹣1,﹣a+1)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图,a∥b,点B在直线b上,且AB⊥BC,若∠1=34°,则∠2的大小为( )
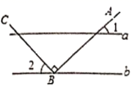 A、34° B、54° C、56° D、66°6. 以下说法中正确的是( )A、若a>|b|,则a2>b2 B、若a>b,则 < C、若a>b,则ac2>bc2 D、若a>b,c>d,则a﹣c>b﹣d7. 《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架. 它的代数成就主要包括开方术、正负术和方程术. 其中方程术是《九章算术》最高的数学成就. 《九章算术》中记载:“今有人共买鸡,人出八,盈三;人出七,不足四. 问人数、鸡价各几何?”译文:“今天有几个人共同买鸡,每人出8钱,多余3钱,每人出7钱,还缺4钱. 问人数和鸡的价钱各是多少?”
A、34° B、54° C、56° D、66°6. 以下说法中正确的是( )A、若a>|b|,则a2>b2 B、若a>b,则 < C、若a>b,则ac2>bc2 D、若a>b,c>d,则a﹣c>b﹣d7. 《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架. 它的代数成就主要包括开方术、正负术和方程术. 其中方程术是《九章算术》最高的数学成就. 《九章算术》中记载:“今有人共买鸡,人出八,盈三;人出七,不足四. 问人数、鸡价各几何?”译文:“今天有几个人共同买鸡,每人出8钱,多余3钱,每人出7钱,还缺4钱. 问人数和鸡的价钱各是多少?”设人数有 人,鸡的价钱是 钱,可列方程组为
 A、 B、 C、 D、8. 已知点M(2m﹣1,1﹣m)在第四象限,则m的取值范围在数轴上表示正确的是( )A、
A、 B、 C、 D、8. 已知点M(2m﹣1,1﹣m)在第四象限,则m的取值范围在数轴上表示正确的是( )A、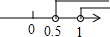 B、
B、 C、
C、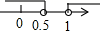 D、
D、 9. 如图所示, ,则 , , 关系正确的是
9. 如图所示, ,则 , , 关系正确的是 A、 B、 C、 D、10. 某公园划船项目收费标准如下:
A、 B、 C、 D、10. 某公园划船项目收费标准如下:船型
两人船
(限乘两人)
四人船
(限乘四人)
六人船
(限乘六人)
八人船
(限乘八人)
每船租金
(元/小时)
90
100
130
150
某班18名同学一起去该公园划船,若每人划船的时间均为1小时,则租船的总费用最低为( )元.
A、370 B、380 C、390 D、410二、填空题
-
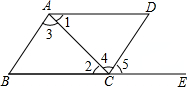
11. 计算: .12. 如图,下列条件中:
①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5;
则一定能判定AB∥CD的条件有(填写所有正确的序号).
 13. 如图,某校根据学生上学方式的一次抽样调查结果,绘制出一个未完成的扇形统计图,若该校共有学生1000人,则根据此估计步行上学的有人.
13. 如图,某校根据学生上学方式的一次抽样调查结果,绘制出一个未完成的扇形统计图,若该校共有学生1000人,则根据此估计步行上学的有人. 14. 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2019次运动后,动点P的坐标是 .
14. 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2019次运动后,动点P的坐标是 . 15. 我市中学生足球比赛,比赛规则是:胜一场积3分,平一场积1分;负一场积0分. 某校足球队共比赛11场,以负1场的成绩夺得了冠军,已知该校足球队最后的积分不少于25分,则该校足球队获胜的场次最少是场.
15. 我市中学生足球比赛,比赛规则是:胜一场积3分,平一场积1分;负一场积0分. 某校足球队共比赛11场,以负1场的成绩夺得了冠军,已知该校足球队最后的积分不少于25分,则该校足球队获胜的场次最少是场.三、解答题
-
16. 计算:(1)、(2)、17.(1)、解方程组:(2)、解不等式组: ,并把解集表示在数轴上.
 18. 已知:如图, , , . 求证: .
18. 已知:如图, , , . 求证: .
请你把书写过程补充完整.
证明:∵ , ,
∴ .
∴__▲_ .
∴ _▲_(_▲_).
∵ ,
∴ .
∴_▲_ _▲_(_▲_).
∴ . (_▲_)
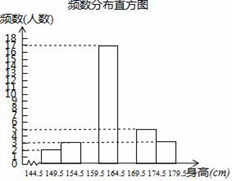
19. 在平面直角坐标系中, 、 、 三点的坐标分别为 , , (1)、在如图的坐标系中画出 ;(2)、 的面积为;(3)、将 平移得到 ,点 经过平移后的对应点为 ,在坐标系内画出 并写出点 , 的坐标.20. 为了解同学们的身体发育情况,学校体卫办公室对七年级全体学生进行了身高测量(精确到1cm),并从中抽取了部分数据进行统计,请根据尚未完成的频数分布表和频数分布直方图解答下列问题:
(1)、在如图的坐标系中画出 ;(2)、 的面积为;(3)、将 平移得到 ,点 经过平移后的对应点为 ,在坐标系内画出 并写出点 , 的坐标.20. 为了解同学们的身体发育情况,学校体卫办公室对七年级全体学生进行了身高测量(精确到1cm),并从中抽取了部分数据进行统计,请根据尚未完成的频数分布表和频数分布直方图解答下列问题:频率分布表
分组
频数
百分比
144.5~149.5
2
4%
149.5~154.5
3
6%
154.5~159.5
a
16%
159.5~164.5
17
34%
164.5~169.5
b
n%
169.5~174.5
5
10%
174.5~179.5
3
6%
 (1)、求a、b、n的值;(2)、补全频数分布直方图;(3)、学校准备从七年级学生中选拔护旗手,要求身高不低于170cm,如果七年级有学生350人,护旗手的候选人大概有多少?21. 今年第37届洛阳牡丹文化节期间龙门石窟旅游景点共接待游客92. 4万人次,和去年同时期相比,游客总数增加了 ,其中省外游客增加了 ,省内游客增加了 .(1)、求该景点去年牡丹文化节期间接待的省外游客和省内游客各是多少万人?(2)、若省外游客每位门票均价约为100元,省内游客每位门票均价约为80元,则今年文化节期间该景点的门票收入大约是多少万元?22. 如图, 、 是直线, , , ,
(1)、求a、b、n的值;(2)、补全频数分布直方图;(3)、学校准备从七年级学生中选拔护旗手,要求身高不低于170cm,如果七年级有学生350人,护旗手的候选人大概有多少?21. 今年第37届洛阳牡丹文化节期间龙门石窟旅游景点共接待游客92. 4万人次,和去年同时期相比,游客总数增加了 ,其中省外游客增加了 ,省内游客增加了 .(1)、求该景点去年牡丹文化节期间接待的省外游客和省内游客各是多少万人?(2)、若省外游客每位门票均价约为100元,省内游客每位门票均价约为80元,则今年文化节期间该景点的门票收入大约是多少万元?22. 如图, 、 是直线, , , ,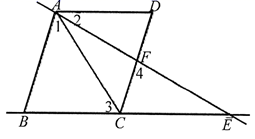 (1)、试判断 与 是否平行,说说你的理由.(2)、若 , ,求 的度数.23. 目前节能灯在城市已基本普及,为响应号召,某商场计划购进甲,乙两种节能灯共200只,这两种节能灯的进价、售价如下表:
(1)、试判断 与 是否平行,说说你的理由.(2)、若 , ,求 的度数.23. 目前节能灯在城市已基本普及,为响应号召,某商场计划购进甲,乙两种节能灯共200只,这两种节能灯的进价、售价如下表:进价(元/只)
售价(元/只)
甲型
20
30
乙型
30
45
(1)、若购进甲,乙两种节能灯共用去5200元,求甲、乙两种节能灯各进多少只?(2)、若商场准备用不多于5400元购进这两种节能灯,问甲型号的节能灯至少进多少只?(3)、在(2)的条件下,该商场销售完200只节能灯后能否实现盈利超过2690元的目标?若能请你给出相应的采购方案;若不能说明理由.