江苏省苏州市昆山市2019-2020学年高一下学期数学期中考试试卷
试卷更新日期:2020-07-15 类型:期中考试
一、单选题
-
1. 直线 的倾斜角为( )A、30° B、60° C、120° D、150°2. 在 中,角 , , 的对边分别为 , , , , , ,则 ( )A、 B、 C、 D、3. 在平面直角坐标系 中,矩形 的顶点坐标分别为 ,则矩形 的外接圆方程是( )A、 B、 C、 D、4. 古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米2016石,验得米内夹谷,抽样取米一把,数得270粒内夹谷30粒,则这批米内夹谷约为( )A、222石 B、224石 C、230石 D、232石5. 已知直线 ,直线 ,若 ,则实数a的值为( )A、 B、4 C、 D、06. 已知 ,点P在x轴上,且使得 取最小值,则点P的坐标为( )A、 B、 C、 D、7. 如图,某侦察飞机在恒定高度沿直线 匀速飞行.在A处观测地面目标A,测得俯角 .经2分钟飞行后在B处观测地面目标P,测得俯角 .又经过一段时间飞行后在 处观察地面目标 ,测得俯角 且 ,则该侦察飞机由B至C的飞行时间为( )
 A、1.25分钟 B、1.5分钟 C、1.75分钟 D、2分钟8. 已知圆C的方程为: ,若直线 上存在一点P,使得在圆C上总存在不同的两点 ,使得 ,则圆C的半径r的取值范围是( )A、 B、 C、 D、
A、1.25分钟 B、1.5分钟 C、1.75分钟 D、2分钟8. 已知圆C的方程为: ,若直线 上存在一点P,使得在圆C上总存在不同的两点 ,使得 ,则圆C的半径r的取值范围是( )A、 B、 C、 D、二、多选题
-
9. 抛掷一枚硬币三次,若记出现“三个正面”、“三个反面”、“二正一反”、“一正二反”的概率分别为 ,则下列结论中正确的是( )A、 B、 C、 D、10. 在同一直角坐标系中,直线 与圆 的位置可能是( )A、
 B、
B、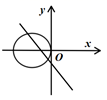 C、
C、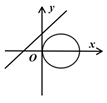 D、
D、 11. 对于 ,有如下判断,其中正确的是( )A、若 ,则 必为等腰三角形 B、若 ,则 C、若 ,则符合条件的 有两个 D、若 ,则 必为钝角三角形12. 在平面直角坐标系 中,已知曲线C的方程是 ,则下列结论正确的是( )A、曲线C关于 对称 B、 的最小值为 C、曲线C的周长为 D、曲线C围成的图形面积为
11. 对于 ,有如下判断,其中正确的是( )A、若 ,则 必为等腰三角形 B、若 ,则 C、若 ,则符合条件的 有两个 D、若 ,则 必为钝角三角形12. 在平面直角坐标系 中,已知曲线C的方程是 ,则下列结论正确的是( )A、曲线C关于 对称 B、 的最小值为 C、曲线C的周长为 D、曲线C围成的图形面积为三、填空题
-
13. 随机抽取圆柱形零件样本5件,测量其直径依次为5.1,4.9,5.2,4.7,5.1(单位: ),则数据5.1,4.9,5.2,4.7,5.1的方差为 .14. 在 中,已知 , , ,则 .15. 在平面直角坐标 中,已知 、 、 ,平面内的点P满足 ,则点P的坐标为 .
四、双空题
-
16. 在平面直角坐标系 内,已知 ,若点P满足 ,则 面积的最大值为;若点 还同时满足 ,则点P的横坐标等于 .
五、解答题
-
17. 在 中,已知 ,且 边的中点M在y轴上, 边的中点N在x轴上.(1)、求顶点C的坐标;(2)、求 的面积.18. 某校高一某班50名学生参加防疫知识竞赛,将所有成绩制作成频率分布表如下:
分组
频数
频率
0.06
35
0.070
6
0.12
4
(1)、求频率分布表中 的值;(2)、从成绩在 的学生中选出2人,请写出所有不同的选法,并求选出2人的成绩都在 中的概率.19. 在锐角 中,角 的对边分別为 ,且 .(1)、求角C的大小;(2)、若 ,且 的面积为 ,求a+b的值.20. 某调查机构为了了解某产品年产量 (吨)对价格 (千元/吨)和年利润 的影响,对近五年该产品的年产量和价格统计如下表,若 .1
2
3
4
5
8
7
6
4
(1)、求表格中c的值;(2)、求y关于x的线性回归方程 ;(3)、若每吨该产品的成本为2千元,假设该产品可全部卖出,预测当年产量为多少时,年利润 取得最大值?
-


