2020年暑期衔接训练青岛版数学八年级下册:第9讲 第七章《实数》单元测试
试卷更新日期:2020-07-15 类型:复习试卷
一、单选题
-
1. 已知 ,则 的值为( )A、 B、 C、 D、2. 将面积为2π的半圆与两个正方形A和正方形B拼接如图所示,这两个正方形面积的和为( )
 A、4 B、8 C、2π D、163. 勾股定理是人类最伟大的科学发现之一,在我国古代算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大的正方形内.若知道图中阴影部分的面积,则一定能求出( )
A、4 B、8 C、2π D、163. 勾股定理是人类最伟大的科学发现之一,在我国古代算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大的正方形内.若知道图中阴影部分的面积,则一定能求出( )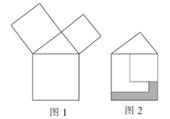 A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和4. 下列等式成立的是( )A、 B、 C、 D、5. 下列说法中正确的有( )
A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和4. 下列等式成立的是( )A、 B、 C、 D、5. 下列说法中正确的有( )①负数没有平方根,但负数有立方根;②一个数的立方根等于它本身,则这个数是0或1;
③无理数与数轴上的点一一对应;④ 的平方根是±2;⑤- 一定是负数
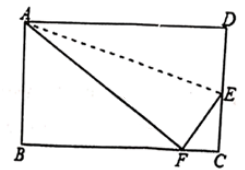
A、1个 B、2个 C、3个 D、4个6. 在△ABC中,∠A,∠B,∠C的对边分别是a、b、c,下列条件中,能判断△ABC是直角三角形( )A、a=2,b=3,c=4 B、a:b:c= C、∠A+∠B=2∠C D、∠A=2∠B=3∠C7. 在实数 ,3.14159, , ,1.010010001···, ,0. 中,无理数的个数是( )A、1 B、2 C、3 D、48. 如图所示的“赵爽弦圈”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为n,较短直角边长为b.若nb=8,大正方形的面积为25,则小正方形的边长为( )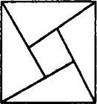 A、9 B、6 C、4 D、39. 如图,将两个大小、形状完全相同的△ABC 和△A′B′C′拼在一起,其中点 A′与点 A 重合,点 C′ 落在边 AB 上,连接 B′C.若∠ACB=∠AC′B′=90°,AC=BC=3,则 B′C 的长为( )
A、9 B、6 C、4 D、39. 如图,将两个大小、形状完全相同的△ABC 和△A′B′C′拼在一起,其中点 A′与点 A 重合,点 C′ 落在边 AB 上,连接 B′C.若∠ACB=∠AC′B′=90°,AC=BC=3,则 B′C 的长为( )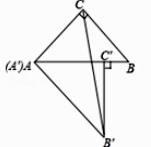 A、 B、6 C、 D、10. 已知:在△ABC中,三边长a,b,c满足等式a2-16b2-c2+6ab+10bc=0,则( )
A、 B、6 C、 D、10. 已知:在△ABC中,三边长a,b,c满足等式a2-16b2-c2+6ab+10bc=0,则( )
A、a<b<c B、a+c=2b C、c<b<a D、a+c与2b的大小关系不能确定11. 把两个同样大小的含45°角的三角尺按如图所示的方式放置,其中一个锐角顶点与另一个的直角顶点重合于点A,且另外三个锐角顶点B,C,D在同一条直线上,若AB= ,则CD的长为( )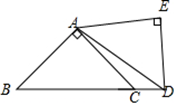 A、
A、 B、
B、 C、
C、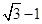 D、
12. 如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→……,白甲壳虫爬行的路线是AB→BB1→……,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数).那么当黑、白两个甲壳虫各爬行完第2018条棱分别停止在所到的正方体顶点处时,它们之间的距离是( )
D、
12. 如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→……,白甲壳虫爬行的路线是AB→BB1→……,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数).那么当黑、白两个甲壳虫各爬行完第2018条棱分别停止在所到的正方体顶点处时,它们之间的距离是( ) A、0 B、
A、0 B、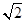 C、
D、1
C、
D、1
二、填空题
-
13. 已知的整数部分为a,小数部分为b,则a-b= .
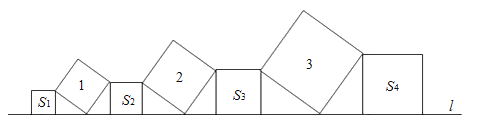
14.在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是S1 , S2 , S3 , S4 , 则S1+S2+S3+S4=
 15. 程大位所著《算法统宗》是一部中国传统数学重要的著作.在《算法统宗》中记载:“平地秋千未起,踏板离地一尺.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”【注释】1步=5尺.
15. 程大位所著《算法统宗》是一部中国传统数学重要的著作.在《算法统宗》中记载:“平地秋千未起,踏板离地一尺.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”【注释】1步=5尺.译文:“当秋千静止时,秋千上的踏板离地有1尺高,如将秋千的踏板往前推动两步(10尺)时,踏板就和人一样高,已知这个人身高是5尺.美丽的姑娘和才子们,每天都来争荡秋千,欢声笑语终日不断.好奇的能工巧匠,能算出这秋千的绳索长是多少吗?”
如图,假设秋千的绳索长始终保持直线状态,OA是秋千的静止状态,A是踏板,CD是地面,点B是推动两步后踏板的位置,弧AB是踏板移动的轨迹.已知AC=1尺,CD=EB=10尺,人的身高BD=5尺.设绳索长OA=OB=x尺,则可列方程为 .
 16. 已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积 .
16. 已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积 . 17. 如图,在高3米,坡面线段AB长为5米的楼梯表面铺地毯,已知楼梯宽1.5米,地毯售价为40元/平方米,若将楼梯表面铺满地毯,则至少需元.
17. 如图,在高3米,坡面线段AB长为5米的楼梯表面铺地毯,已知楼梯宽1.5米,地毯售价为40元/平方米,若将楼梯表面铺满地毯,则至少需元.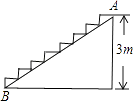 18. 如图,要使宽为2米的矩形平板车ABCD通过宽为2 米的等宽的直角通道,平板车的长不能超过米.
18. 如图,要使宽为2米的矩形平板车ABCD通过宽为2 米的等宽的直角通道,平板车的长不能超过米. 19. 如图1,Rt△ABC中,∠ACB=90°,AC=1,BC=2,将△ABC放置在平面直角坐标系中,使点A与原点重合,点C在x轴正半轴上.将△ABC按如图2方式顺时针滚动(无滑动),则滚动2017次后,点B的坐标为 .
19. 如图1,Rt△ABC中,∠ACB=90°,AC=1,BC=2,将△ABC放置在平面直角坐标系中,使点A与原点重合,点C在x轴正半轴上.将△ABC按如图2方式顺时针滚动(无滑动),则滚动2017次后,点B的坐标为 . 20. 分析探索题:细心观察如图,认真分析各式,然后解答问题.
20. 分析探索题:细心观察如图,认真分析各式,然后解答问题.OA22=()2+1=2 S1=;
OA32=()2+1=3 S2=;
OA42=()2+1=4 S3=…
(1)请用含有n(n为正整数)的等式Sn= ;
(2)推算出OA10=
(3)求出 S12+S22+S32+…+S102的值.

三、计算题
-
21. 求x的值:(1)、(x﹣2)2=81(2)、(2x﹣1)3+27=0(3)、计算: ;22. 已知2是 的平方根, 是 的立方根,求 的平方根.23. 课堂上老师讲解了比较 和 的方法,观察发现11-10=15-14=1,于是比较这两个数的倒数:
因为 ,所以 ,则有 ,
请你设计一种方法比较 与 的大小,
四、作图题
-
24. 如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫格点.
 (1)、在图1中以格点为顶点画一个直角三角形,使它的三边长都为整数;(2)、在图2中以格点为顶点画一个直角三角形,使它的三边长都为无理数;(3)、在图3中以格点为顶点画一个面积为10的正方形.
(1)、在图1中以格点为顶点画一个直角三角形,使它的三边长都为整数;(2)、在图2中以格点为顶点画一个直角三角形,使它的三边长都为无理数;(3)、在图3中以格点为顶点画一个面积为10的正方形.五、解答题
-
25. 如图所示,北部湾海面有一艘解放军军舰正在基地 的正东方向且距 地40海里的 处训练,突然接到基地命令,要该舰前往 岛接送一名患病的渔民到基地 的医院救治.已知 岛在基地 的北偏东58°方向且距基地 32海里,在 处的北偏西32°的方向上.军舰从 处出发,平均每小时行驶40海里,问至少需要多长时间能把患病渔民送到基地医院?
 26. 如图,在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13米,此人以0.5米每秒的速度收绳,10秒后船移动到点D的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号)
26. 如图,在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13米,此人以0.5米每秒的速度收绳,10秒后船移动到点D的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号)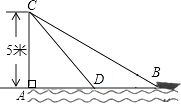
-