天津市津南区2020年中考数学一模试卷
试卷更新日期:2020-07-14 类型:中考模拟
一、单选题
-
1. 计算 的值是( )A、-12 B、-2 C、35 D、-352. tan60°的值等于( )A、 B、 C、 D、3. 2019年10月1日上午,庆祝中华人民共和国成立70周年在北京天安门广场隆重举行阅兵活动.由人民解放军、武警部队和民兵预备役部队约15000名官兵接受检阅.将15000用科学记数法可表示为( )A、 B、 C、 D、4. 下列图形中,可以看作轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5.
5.如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )
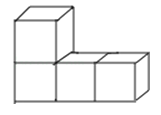 A、
A、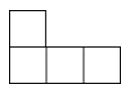 B、
B、 C、
C、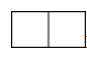 D、
D、 6. 估计 的值在( )A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间7. 计算 的结果为( )A、1 B、2 C、 D、8. 方程组 的解是( )A、 B、 C、 D、9. 若点 , , 都在反比例函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、10. 如图,四边形 为平行四边形,A , C两点的坐标分别是 , ,则平行四边形 的周长等于( )
6. 估计 的值在( )A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间7. 计算 的结果为( )A、1 B、2 C、 D、8. 方程组 的解是( )A、 B、 C、 D、9. 若点 , , 都在反比例函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、10. 如图,四边形 为平行四边形,A , C两点的坐标分别是 , ,则平行四边形 的周长等于( )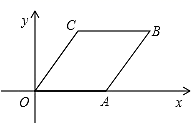 A、 B、 C、 D、11. 如图,将 沿 方向平移得到 ,使点B的对应点E恰好落在边 的中点上,点C的对应点F在 的延长线上,连接 .下列结论一定正确的是( )
A、 B、 C、 D、11. 如图,将 沿 方向平移得到 ,使点B的对应点E恰好落在边 的中点上,点C的对应点F在 的延长线上,连接 .下列结论一定正确的是( )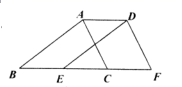 A、 B、 C、 D、 平分12. 二次函数 ( , , 是常数, )的自变量x与函数值y的部分对应值如下表:
A、 B、 C、 D、 平分12. 二次函数 ( , , 是常数, )的自变量x与函数值y的部分对应值如下表:…
-1
0
1
3
…
…
3
3
…
且当 时,与其对应的函数值 .有下列结论:① ;②3是关于 的方程 的一个根;③ .其中,正确结论的个数是( )
A、0 B、1 C、2 D、3二、填空题
-
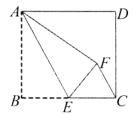
13. 计算 的结果等于 .14. 计算 的结果等于 .15. 不透明袋子中装有12个球,其中有5个红球、4个绿球和3个蓝球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是红球的概率是 .16. 一次函数 ,y随x的增大而减小,则k的值可以是(写出一个即可).17. 如图,正方形纸片 的边长为5,E是边 的中点,连接 .沿 折叠该纸片,使点B落在F点.则 的长为 .
三、解答题
-
18. 如图,在每个小正方形的边长为1的网格中, 的顶点 , , 均在格点上.
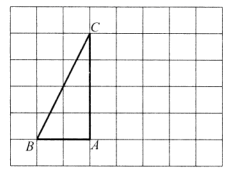 (1)、 的长等于;(2)、在如图所示的网格中,将 绕点A旋转,使得点B的对应点 落在边 上,得到 ,请用无刻度的直尺,画出 ,并简要说明这个三角形的各个顶点是如何找到的(不要求证明).19. 解不等式组
(1)、 的长等于;(2)、在如图所示的网格中,将 绕点A旋转,使得点B的对应点 落在边 上,得到 ,请用无刻度的直尺,画出 ,并简要说明这个三角形的各个顶点是如何找到的(不要求证明).19. 解不等式组请结合题意填空,完成本题的解答.
(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来: (4)、原不等式组的解集为 .20. 在某中学开展的“好书伴我成长”读书活动中,为了解八年级320名学生读书情况,随机调查了八年级部分学生读书的册数.根据调查结果绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
(4)、原不等式组的解集为 .20. 在某中学开展的“好书伴我成长”读书活动中,为了解八年级320名学生读书情况,随机调查了八年级部分学生读书的册数.根据调查结果绘制出如下的统计图①和图②.请根据相关信息,解答下列问题: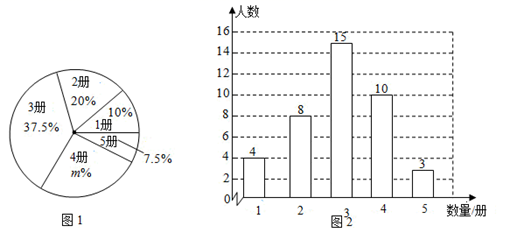 (1)、本次接受调查的学生人数为 , 图①中m的值为;(2)、求统计的这组数据的平均数、众数和中位数;(3)、根据统计的样本数据,估计该校读书超过3册的学生人数.21. 已知: 内接于 , ,P是 外一点.
(1)、本次接受调查的学生人数为 , 图①中m的值为;(2)、求统计的这组数据的平均数、众数和中位数;(3)、根据统计的样本数据,估计该校读书超过3册的学生人数.21. 已知: 内接于 , ,P是 外一点. (1)、如图①,点P在 上,若 ,求 和 的大小;(2)、如图②,点P在 外, 是 的直径, 与 相切于点B , 若 ,求 的大小.22. 数学兴趣小组活动课上测量电线杆的高度.在位于电线杆同侧的A、B处(点A、B及电线杆底部F在同一条直线上),测得电线杆顶部E的仰角分别为36°和45°(如图所示).已知测量仪器距离地面都是1.5m,两测点A、B的距离是12m,求电线杆 的高度( ,结果精确到0.1m)
(1)、如图①,点P在 上,若 ,求 和 的大小;(2)、如图②,点P在 外, 是 的直径, 与 相切于点B , 若 ,求 的大小.22. 数学兴趣小组活动课上测量电线杆的高度.在位于电线杆同侧的A、B处(点A、B及电线杆底部F在同一条直线上),测得电线杆顶部E的仰角分别为36°和45°(如图所示).已知测量仪器距离地面都是1.5m,两测点A、B的距离是12m,求电线杆 的高度( ,结果精确到0.1m)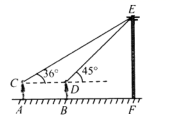 23. 某剧院举行专场音乐会,成人票每张20元,学生票每张5元.暑假期间,为了丰富广大师生的业余文化生活,影剧院制定了两种优惠方案,方案一:购买一张成人票赠送一张学生票;方案二:按总价的90%付款.某校有4名老师带队,与若干名(不少于4人)学生一起听音乐会.设学生人数为x人, (x为整数).(1)、根据题意填表:
23. 某剧院举行专场音乐会,成人票每张20元,学生票每张5元.暑假期间,为了丰富广大师生的业余文化生活,影剧院制定了两种优惠方案,方案一:购买一张成人票赠送一张学生票;方案二:按总价的90%付款.某校有4名老师带队,与若干名(不少于4人)学生一起听音乐会.设学生人数为x人, (x为整数).(1)、根据题意填表:学生人数/人
4
10
20
…
方案一付款金额/元
80
110
…
方案二付款金额/元
90
117
…
(2)、设方案一付款总金额为 元,方案二付款总金额为 元,分别求 , 关于x的函数解析式;(3)、根据题意填空:①若用两种方案购买音乐会的花费相同,则听音乐会的学生有人;
②若有60名学生听音乐会,则用方案购买音乐会票的花费少;
③若用一种方案购买音乐会票共花费了450元,则用方案购买音乐会票,使听音乐的学生人数多.
24. 将一个矩形纸片 放置在平面直角坐标系中,点 ,点 ,点E , F分别在边 , 上.沿着 折叠该纸片,使得点A落在 边上,对应点为 ,如图①.再沿 折叠,这时点E恰好与点C重合,如图②.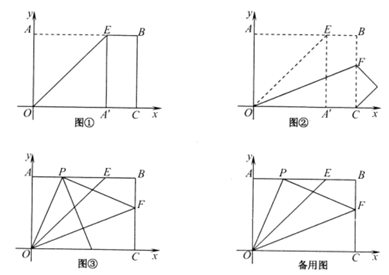 (1)、求点C的坐标;(2)、将该矩形纸片展开,再折叠该矩形纸片,使点O与点F重合,折痕与 相交于点P , 展开矩形纸片,如图③.
(1)、求点C的坐标;(2)、将该矩形纸片展开,再折叠该矩形纸片,使点O与点F重合,折痕与 相交于点P , 展开矩形纸片,如图③.①求 的大小;
②点M , N分别为 , 上的动点,当 取得最小值时,求点N的坐标(直接写出结果即可).
25. 已知抛物线 ,与x轴交于两点A , B(点A在点B的左侧),与y轴交于点C .(1)、求点A , B和点C的坐标;(2)、已知P是线段 上的一个动点.①若 轴,交抛物线于点Q , 当 取最大值时,求点P的坐标;
②求 的最小值.