天津市河东区2020年中考数学一模试卷
试卷更新日期:2020-07-14 类型:中考模拟
一、单选题
-
1. 计算:(﹣3)×5的结果是( )A、﹣15 B、15 C、﹣2 D、22. 的值为( )A、 B、 C、 D、3. 下面图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 我国最长的河流长江全长约为6400千米,用科学记数法表示为( )A、 米 B、 米 C、 米 D、 米5. 下列几何体是由4个相同的小正方体搭成的,其中左视图与主视图相同的是A、
4. 我国最长的河流长江全长约为6400千米,用科学记数法表示为( )A、 米 B、 米 C、 米 D、 米5. 下列几何体是由4个相同的小正方体搭成的,其中左视图与主视图相同的是A、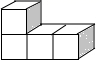 B、
B、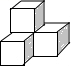 C、
C、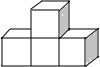 D、
D、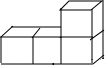 6. 下列整数中,与 最接近的是( )A、4 B、5 C、6 D、77. 化简 的结果是( )A、A B、a+1 C、a﹣1 D、a2﹣18. 如图,已知在平面直角坐标系中,四边形ABCD是菱形,其中B点坐标是(8,2),D点坐标是(0,2),点A在x轴上,则菱形ABCD的周长是( )
6. 下列整数中,与 最接近的是( )A、4 B、5 C、6 D、77. 化简 的结果是( )A、A B、a+1 C、a﹣1 D、a2﹣18. 如图,已知在平面直角坐标系中,四边形ABCD是菱形,其中B点坐标是(8,2),D点坐标是(0,2),点A在x轴上,则菱形ABCD的周长是( ) A、2 B、8 C、8 D、129. 关于 , 的方程组 的解为 则( )A、 , B、 , C、 , D、 ,10. 已知点 , , 都在反比例函数 的图象上,那么 , 与 的大小关系是( )A、 B、 C、 D、11. 如图,矩形ABCD中,AB=8,BC=6,将矩形ABCD绕点A逆时针旋转得到矩形AEFG,AE,FG分别交射线CD于点PH,连结AH,若P是CH的中点,则△APH的周长为( )
A、2 B、8 C、8 D、129. 关于 , 的方程组 的解为 则( )A、 , B、 , C、 , D、 ,10. 已知点 , , 都在反比例函数 的图象上,那么 , 与 的大小关系是( )A、 B、 C、 D、11. 如图,矩形ABCD中,AB=8,BC=6,将矩形ABCD绕点A逆时针旋转得到矩形AEFG,AE,FG分别交射线CD于点PH,连结AH,若P是CH的中点,则△APH的周长为( )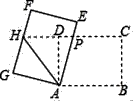 A、15 B、18 C、20 D、2412. 如图所示,已知二次函数 的图象与 轴交于点 ,与 轴交于点 , ,对称轴为直线 ,则下列结论:① ;② ;③ ;④ 是关于 的一元二次方程 的一个根.其中正确的有( )
A、15 B、18 C、20 D、2412. 如图所示,已知二次函数 的图象与 轴交于点 ,与 轴交于点 , ,对称轴为直线 ,则下列结论:① ;② ;③ ;④ 是关于 的一元二次方程 的一个根.其中正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
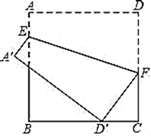
13. 若 .14. 计算 .15. 为庆祝新中国成立70周年,某校开展以“我和我亲爱的祖国”为主题的“快闪”活动,七年级准备从两名男生和三名女生中选出一名同学领唱,如果每一位同学被选中的机会均等,则选出的恰为女生的概率是 .16. 若直线 经过点 ,则该直线不经过第象限.17. 如图,正方形 的边长是9,点 是 边上的一个动点,点 是 边上一点, ,连接 ,把正方形 沿 折叠,使点 , 分别落在点 , 处,当点 落在线段 上时,线段 的长为 .
 18. 如图,在由边长都为1的小正方形组成的网格中,点 , , 均为格点, , , , 为 中点, 为 上的一个动点.
18. 如图,在由边长都为1的小正方形组成的网格中,点 , , 均为格点, , , , 为 中点, 为 上的一个动点. (1)、当点 为线段 中点时, 的长度等于;(2)、将点 绕点 逆时针旋转90°得到点 ,连 ,当线段 取得最小值时,请借助无刻度直尺在给定的网格中画出点 ,点 ,并简要说明你是怎么画出点 ,点 的:.
(1)、当点 为线段 中点时, 的长度等于;(2)、将点 绕点 逆时针旋转90°得到点 ,连 ,当线段 取得最小值时,请借助无刻度直尺在给定的网格中画出点 ,点 ,并简要说明你是怎么画出点 ,点 的:.三、解答题
-
19. 解不等式组
请结合题意填空,完成本题的解答.
(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上分别表示出来: (4)、原不等式组的解集为 .20. 某校为了解全校学生假期主题阅读的情况(要求每名学生的文章阅读篇数,最少3篇,最多7篇),随机抽查了部分学生在某一周主题阅读文章的篇数,并制成下列统计图表.
(4)、原不等式组的解集为 .20. 某校为了解全校学生假期主题阅读的情况(要求每名学生的文章阅读篇数,最少3篇,最多7篇),随机抽查了部分学生在某一周主题阅读文章的篇数,并制成下列统计图表.某校抽查的学生文章阅读的篇数统计表
文章阅读的篇数(篇)
3
4
5
6
7
人数(人)
20
28
16
12

请根据统计图表中的信息,解答下列问题:
(1)、求被抽查的学生人数和 的值;(2)、求本次抽查的学生文章阅读篇数的中位数和众数;(3)、若该校共有800名学生,根据抽查结果,估计该校学生读书总数.21. 如图,在 中,点 为弧 的中点,过点 作 的切线 ,交弦 的延长线于点 .(1)、如图①,连接 ,若 ,求 的大小; (2)、如图②,连接 ,若 , ,求 的度数.
(2)、如图②,连接 ,若 , ,求 的度数. 22. 如图,某办公楼AB的右边有一建筑物CD,在建设物CD离地面2米高的点E处观测办公楼顶A点,测得的仰角 = ,在离建设物CD 25米远的F点观测办公楼顶A点,测得的仰角 = (B,F,C在一条直线上).
22. 如图,某办公楼AB的右边有一建筑物CD,在建设物CD离地面2米高的点E处观测办公楼顶A点,测得的仰角 = ,在离建设物CD 25米远的F点观测办公楼顶A点,测得的仰角 = (B,F,C在一条直线上).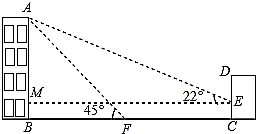 (1)、求办公楼AB的高度;(2)、若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.(参考数据: )23. 下表中给出 , , 三种手机通话的收费方式.
(1)、求办公楼AB的高度;(2)、若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.(参考数据: )23. 下表中给出 , , 三种手机通话的收费方式.收费方式
月通话费/元
包时通话时间/
超时费/(元/ )
不限时
(1)、设月通话时间为 小时,则方案 , , 的收费金额 , , 都是 的函数,请分别求出这三个函数解析式.(2)、填空:若选择方式 最省钱,则月通话时间 的取值范围为;
若选择方式 最省钱,则月通话时间 的取值范围为;
若选择方式 最省钱,则月通话时间 的取值范围为;
(3)、小王、小张今年 月份通话费均为 元,但小王比小张通话时间长,求小王该月的通话时间.24. 平面直角坐标系中, 是等边三角形,点 ,点 ,点 是 边上的一个动点(与点 、 不重合).直线 是经过点 的一条直线,把 沿直线 折叠,点 的对应点是点 .(1)、如图①,当 时,若直线 ,求点 的坐标; (2)、如图②,当点 在 边上运动时,若直线 ,求 的面积;
(2)、如图②,当点 在 边上运动时,若直线 ,求 的面积; (3)、当 时,在直线 变化过程中,求 面积的最大值(直接写出结果即可).25. 如图,抛物线 与 轴分别交于点 , ,与 轴交于点 .
(3)、当 时,在直线 变化过程中,求 面积的最大值(直接写出结果即可).25. 如图,抛物线 与 轴分别交于点 , ,与 轴交于点 . (1)、求抛物线的解析式;(2)、设点 在第一象限的抛物线上,连接 , .试问,在对称轴左侧的抛物线是否存在一点 ,满足 ?如果存在,请求出点 的坐标:如果不存在,请明理由;(3)、存在正实数 , ( ),当 时,恰好满足 ,求 , 的值.
(1)、求抛物线的解析式;(2)、设点 在第一象限的抛物线上,连接 , .试问,在对称轴左侧的抛物线是否存在一点 ,满足 ?如果存在,请求出点 的坐标:如果不存在,请明理由;(3)、存在正实数 , ( ),当 时,恰好满足 ,求 , 的值.