天津市和平区2020年中考数学二模试卷
试卷更新日期:2020-07-14 类型:中考模拟
一、单选题
-
1. 计算(﹣2)3﹣(﹣2)2的结果是( )A、﹣4 B、4 C、12 D、﹣122. 2sin60°的值等于( )A、1 B、 C、 D、3. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、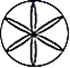 C、
C、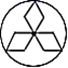 D、
D、 4. 2016年某市用于资助贫困学生的助学金总额是9680000元,将9680000用科学记数法表示为( )A、96.8×105 B、9.68×106 C、9.68×107 D、0.968×1085. 在水平的讲台上放置圆柱形水杯和长方体形粉笔盒(如图),则从正面看得到的平面图形是( )
4. 2016年某市用于资助贫困学生的助学金总额是9680000元,将9680000用科学记数法表示为( )A、96.8×105 B、9.68×106 C、9.68×107 D、0.968×1085. 在水平的讲台上放置圆柱形水杯和长方体形粉笔盒(如图),则从正面看得到的平面图形是( )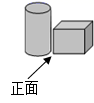 A、
A、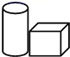 B、
B、 C、
C、 D、
D、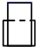 6. 估计 的值在( )A、5和6之间 B、6和7之间 C、7和8之间 D、8和9之间7. 化简 的结果是( )A、x+1 B、 C、x﹣1 D、8. 已知 是方程组 的解,则 的值是( )A、﹣1 B、1 C、﹣5 D、59. 如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( )
6. 估计 的值在( )A、5和6之间 B、6和7之间 C、7和8之间 D、8和9之间7. 化简 的结果是( )A、x+1 B、 C、x﹣1 D、8. 已知 是方程组 的解,则 的值是( )A、﹣1 B、1 C、﹣5 D、59. 如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( ) A、 B、6 C、4 D、510. 反比例函数 图象上有三个点(x1 , y1),(x2 , y2),(x3 , y3),其中x1<x2<0<x3 , 则y1 , y2 , y3的大小关系是( )A、 B、 C、 D、11. 如右图,正方形ABCD的边长为2,点E是BC边上一点,以AB为直径在正方形内作半圆O,将△DCE沿DE翻折,点C刚好落在半圆O的点F处,则CE的长为( )
A、 B、6 C、4 D、510. 反比例函数 图象上有三个点(x1 , y1),(x2 , y2),(x3 , y3),其中x1<x2<0<x3 , 则y1 , y2 , y3的大小关系是( )A、 B、 C、 D、11. 如右图,正方形ABCD的边长为2,点E是BC边上一点,以AB为直径在正方形内作半圆O,将△DCE沿DE翻折,点C刚好落在半圆O的点F处,则CE的长为( )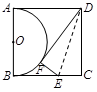 A、 B、 C、 D、12. 已知二次函数y1=mx2+4mx﹣5m(m≠0),一次函数y2=2x﹣2,有下列结论:
A、 B、 C、 D、12. 已知二次函数y1=mx2+4mx﹣5m(m≠0),一次函数y2=2x﹣2,有下列结论:①当x>﹣2时,y随x的增大而减小;
②二次函数y1=mx2+4mx﹣5m(m≠0)的图象与x轴交点的坐标为(﹣5,0)和(1,0);
③当m=1时,y1≤y2;
④在实数范围内,对于x的同一个值,这两个函数所对应的函数值y2≤y1均成立,则m .
其中,正确结论的个数是( )
A、0 B、1 C、2 D、3二、填空题
-
13. 计算 的结果等于.14. 计算 的结果等于.15. 一枚质地均匀的骰子的6个面上分别刻有1〜6的点数,抛掷这枚骰子1次,向上一面的点数大于2且小于5的概率是.16. 如图,在平面直角坐标系中,点O为坐标原点,菱形ABCD的顶点B在x轴的正半轴上,点A坐标为(-4,0),点D的坐标为(-1,4),反比例函数 的图象恰好经过点C,则k的值为.
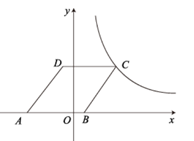 17. 如图,△ABC是等边三角形,AB=3,点E在AC上,AE AC , D是BC延长线上一点,将线段DE绕点E逆时针旋转90°得到线段FE , 当AF∥BD时,线段AF的长为 .
17. 如图,△ABC是等边三角形,AB=3,点E在AC上,AE AC , D是BC延长线上一点,将线段DE绕点E逆时针旋转90°得到线段FE , 当AF∥BD时,线段AF的长为 .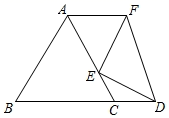
三、解答题
-
18. 如图,在每个小正方形的边长为1的网格中, , , 为格点, 为小正方形边的中点.
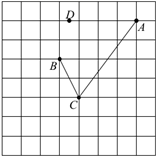 (1)、 的长等于;(2)、点 , 分别为线段 , 上的动点,当 取得最小值时,请在如图所示的网格中,用无刻度的直尺,画出线段 , ,并简要说明点 和点 的位置是如何找到的(不要求证明).19. 解不等式组
(1)、 的长等于;(2)、点 , 分别为线段 , 上的动点,当 取得最小值时,请在如图所示的网格中,用无刻度的直尺,画出线段 , ,并简要说明点 和点 的位置是如何找到的(不要求证明).19. 解不等式组请结合题意填空,完成本题的解答.
(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来: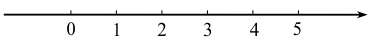 (4)、原不等式组的解集为.20. 某校对九年一班50名学生进行长跑项目的测试,根据测试成绩制作了两个统计图.
(4)、原不等式组的解集为.20. 某校对九年一班50名学生进行长跑项目的测试,根据测试成绩制作了两个统计图.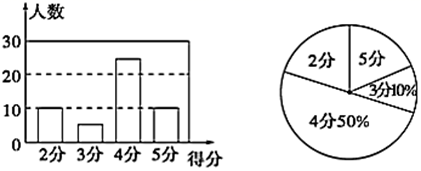
请根据相关信息,解答下列问题:
(1)、本次测试的学生中,得3分的学生有人,得4分的学生有人;(2)、求这50个数据的平均数、众数和中位数.21. 如图,AC是⊙O的直径,PA、PB是⊙O的切线,切点分别是点A、B (1)、如图1,若∠BAC=25°,求∠P的度数.(2)、如图2,若M是劣弧AB上一点,∠AMB=∠AOB , 求∠P的度数.22. 如图,两座建筑物的水平距离 为 .从 点测得 点的仰角 为53° ,从 点测得 点的俯角 为37° ,求两座建筑物的高度(参考数据:
(1)、如图1,若∠BAC=25°,求∠P的度数.(2)、如图2,若M是劣弧AB上一点,∠AMB=∠AOB , 求∠P的度数.22. 如图,两座建筑物的水平距离 为 .从 点测得 点的仰角 为53° ,从 点测得 点的俯角 为37° ,求两座建筑物的高度(参考数据: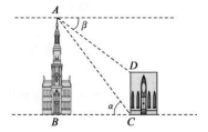 23. 某游泳馆推出了两种收费方式.
23. 某游泳馆推出了两种收费方式.方式一:顾客先购买会员卡,每张会员卡200元,仅限本人一年内使用,凭卡游泳,每次游泳再付费30元.
方式二:顾客不购买会员卡,每次游泳付费40元.
设小亮在一年内来此游泳馆游泳的次数为 次( 为正整数).
(1)、根据题意,填写下表:游泳次数
5
10
15
…
方式一的总费用(元)
350
650
…
方式二的总费用(元)
200
400
…
(2)、若小亮计划今年游泳的总费用为2000元,选择哪种付费方式,他游泳的次数比较多;(3)、当 时,小亮选择哪种付费方式更合算.并说明理由.24. 在平面直角坐标系中,△ABC是直角三角形,∠ABC=90°,∠CAB=60°,点O(0,0),点A(1,0),点B(﹣1,0),点C在第二象限,点P(﹣2, ).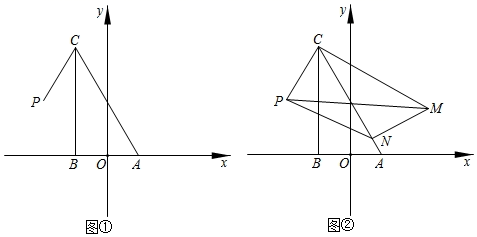 (1)、如图①,求C点坐标及∠PCB的大小;(2)、将△ABC绕C点逆时针旋转得到△MNC,点A,B的对应点分别为点M,N,S为△PMN的面积.
(1)、如图①,求C点坐标及∠PCB的大小;(2)、将△ABC绕C点逆时针旋转得到△MNC,点A,B的对应点分别为点M,N,S为△PMN的面积.①如图②,当点N落在边CA上时,求S的值;
②求S的取值范围(直接写出结果即可).
25. 在平面直角坐标系中,抛物线 经过点 和点 .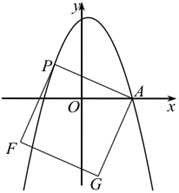 (1)、求抛物线的解析式;(2)、 为抛物线上的一个动点,点 关于原点的对称点为 .当点 落在该抛物线上时,求 的值;(3)、 是抛物线上一动点,连接 ,以 为边作图示一侧的正方形 ,随着点 的运动,正方形的大小与位置也随之改变,当顶点 或 恰好落在 轴上时,求对应的 点坐标.
(1)、求抛物线的解析式;(2)、 为抛物线上的一个动点,点 关于原点的对称点为 .当点 落在该抛物线上时,求 的值;(3)、 是抛物线上一动点,连接 ,以 为边作图示一侧的正方形 ,随着点 的运动,正方形的大小与位置也随之改变,当顶点 或 恰好落在 轴上时,求对应的 点坐标.