天津市北辰区2020年中考数学二模试卷

试卷更新日期：2020-07-14 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算：(﹣3)×5的结果是（）

A、﹣15 B、15 C、﹣2 D、2

查看试题解析
2. cos60°的值等于（）

A、 $\sqrt{3}$ B、1 C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{1}{2}$

查看试题解析
3. 下面的图形，既可以看作是轴对称图形，又可以看作是中心对称图形的是（）.

A、 B、 C、 D、

查看试题解析
4. 1970年4月24日，我国自行设计、制造的第一颗人造地球卫星“东方红一号”成功发射，它的运行轨道，距地球最近点为439000 m，将439000用科学记数法表示应为（）.

A、 $0.439 \times 10^{6}$ B、 $x \leq 3$ C、 $43.9 \times 10^{4}$ D、 $439 \times 10^{3}$

查看试题解析
5. 如图是由4个相同的小正方体组成的立体图形，它的主视图是（）

A、 B、 C、 D、

查看试题解析
6. 估计 $\sqrt{38}$ 的值在（）

A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间

查看试题解析
7. 计算 $\frac{2 a}{a + 1} + \frac{2}{a + 1}$ 的结果是（）.

A、 $2$ B、 $a + 1$ C、 $\frac{2}{a + 1}$ D、 $\frac{1}{a + 1}$

查看试题解析
8. 方程组 ${\begin{array}{l} x - y = 1 \\ x + 3 y = 9 \end{array}$ 的解是（）.

A、 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ B、 ${\begin{array}{l} x = 3 \\ y = 2 \end{array}$ C、 ${\begin{array}{l} x = 4 \\ y = 3 \end{array}$ D、 ${\begin{array}{l} x = 2 \\ y = 3 \end{array}$

查看试题解析
9. 已知点A（ $- 1$ ， $y_{1}$ ），B（ $2$ ， $y_{2}$ ），C（ $3$ ， $y_{3}$ ）在反比例函数 $y = - \frac{6}{x}$ 的图象上，则， $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）.

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{2} < y_{3} < y_{1}$ C、 $y_{3} < y_{2} < y_{1}$ D、 $y_{2} < y_{1} < y_{3}$

查看试题解析
10. 如图，在菱形ABCD中，对角线AC，BD相交于点O，AC=16，BD=4. 平移 $△ A O D$ ，使点D与点B 重合，点A的对应点E落在CB的延长线上，点O的对应点F落在DB的延长线上，则DE的长是（）

A、6 B、8 C、10 D、12

查看试题解析
11. 如图，在 Rt△ABC 中，∠ACB=90°，CD⊥AB，D为垂足. E是AB边上的一个动点，以CE，BE为邻边画平行四边形CEBF，则下列线段的长等于对角线EF最小值的是（）.

A、AC B、BC C、CD D、 $\frac{1}{2}$ AB

查看试题解析
12. 抛物线 $y = a x^{2} + b x + c$ （ $a$ ， $b$ ， $c$ 是常数， $a \neq 0$ ）经过点A（ $1$ ， $0$ ）和点B （ $0$ ， $- 2$ ），且抛物线的对称轴在 $y$ 轴的左侧. 下列结论： ① $a b c < 0$ ； ② 方程 $a x^{2} + (b - 1) x + c = 0$ 有两个不等的实数根； ③ $- 2 < a - b < 2$ . 其中，正确结论的个数是（）

A、0 B、1 C、2 D、3

查看试题解析

二、填空题

13. 计算 $a^{6} \div a^{3}$ 的结果等于.

查看试题解析
14. 计算 $(4 + \sqrt{3}) (4 - \sqrt{3})$ 的结果等于．

查看试题解析
15. 不透明袋子中有2个红球、3个绿球和4个蓝球，这些球除颜色外无其他差别.从袋子中随机取出一个球，则取出的这个球是红球的概率是.

查看试题解析
16. 一次函数 $y = 2 x + 3$ 的图象可由直线 $y = 2 x$ 向上平移得到，则平移的单位长度是.

查看试题解析
17. 如图，矩形纸片ABCD中，AB=4，BC=10，G是BC边上一点，沿AG折叠△ABG，点B的落点为P，GP交AD于点E. 若E是AD的中点，则BG的长是.

查看试题解析

三、解答题

18. 如图，在每个小正方形的边长为 $1$ 的网格中，点A，B，C在格点上，以点A为圆心、AC为半径的半圆交AB于点 E．

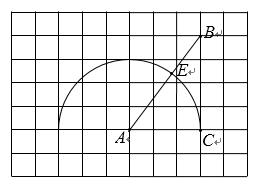(1)、BE的长为；

(2)、请用无刻度的直尺，在如图所示的网格中，找一点P（点P，C 在AB两侧），使PA=5，PE与半圆相切. 简要说明点P的位置是如何找到的．

查看试题解析
19. 解不等式组 ${\begin{array}{l} x + 1 \leq 2 \dots ① \\ 4 x \leq 5 x + 2 \dots ② \end{array}$ 请结合题意填空，完成本题的解答．

(1)、解不等式①，得；

(2)、解不等式②，得；

(3)、把不等式①和②的解集在数轴上表示出来：

(4)、原不等式组的解集为.

查看试题解析
20. 学校为了解全校学生参加社会实践活动情况，随机调查了部分学生一学期参加社会实践活动的时间（单位：天），并用得到的数据绘制了统计图（1）和图（2）. 请根据图中提供的信息，回答下列问题：

(1)、本次随机调查的学生人数是，图（1）中m的值是；

(2)、求调查获取的学生社会实践活动时间样本数据的众数、中位数和平均数；

(3)、该校有480名学生，根据获取的社会实践活动时间样本数据，估计该校一学期社会实践活动时间大于10天的学生人数．

查看试题解析
21. 在⊙O中，半径OA丄OB，点D在OA或OA的延长线上（不与点O，A重合），直线BD交⊙O于点C，过C作⊙O的切线交直线OA于点P.

(1)、如图（1），点D在线段OA上，若∠OBC=15°，求∠OPC的大小；

(2)、如图（2），点D在OA的延长线上，若∠OBC=65°，求∠OPC的大小.

查看试题解析
22. 如图，某旅游景区为方便游客，修建了一条东西走向的栈道AB，栈道AB与景区道路CD平行．在C处测得栈道一端A位于北偏西45°方向，在D处测得栈道另一端B位于北偏东32°方向．已知AC＝60 m ，CD＝46 m，求栈道AB的长（结果保留整数）．参考数据：sin32° ≈ 0.53，cos32° ≈ 0.85，tan32° ≈ 0.62， $\sqrt{2}$ ≈ 1.414.

查看试题解析
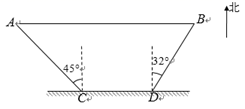23. 甲、乙两个种子店都销售“黄金1号”玉米种子．在甲店，该种子的价格为5元/kg，如果一次购买2kg以上的种子，超过2kg部分的种子的价格打8折．在乙店，不论一次购买该种子的数量是多少，价格均为4.5元/kg．

(1)、根据题意，填写下表：

(2)、设一次购买种子的数量为 $x$ kg（ $x \geq 0$ ）.在甲店购买的付款金额记为 $y_{1}$ 元，在乙店购买的付款金额为 $y_{2}$ 元，分别求 $y_{1}$ ， $y_{2}$ 关于 $x$ 的函数解析式；

(3)、若在同一店中一次购买种子的付款金额是36元，则最多可购买种子kg.若在同一店中一次购买种子10kg，则最少付款金额是元.

查看试题解析
24. 平面直角坐标系中，四边形OABC是正方形，点A，C 在坐标轴上，点B（ $6$ ， $6$ ），P是射线OB上一点，将 $△ A O P$ 绕点A顺时针旋转90°，得 $△ A B Q$ ，Q是点P旋转后的对应点.

(1)、如图（1）当OP = $2 \sqrt{2}$ 时，求点Q的坐标；

(2)、如图（2），设点P（ $x$ ， $y$ ）（ $0 < x < 6$ ）， $△ A P Q$ 的面积为S. 求S与 $x$ 的函数关系式，并写出当S取最小值时，点P的坐标；

(3)、当BP+BQ = $8 \sqrt{2}$ 时，求点Q的坐标（直接写出结果即可）

查看试题解析
25. 在平面直角坐标系中，抛物线 $y = - m x^{2} + 2 m x + 3 m$ （ $m > 0$ ）与 $x$ 轴交于A、B两点（点B在A的右侧），与 $y$ 轴交于点C，D是抛物线的顶点.

(1)、当 $m = 1$ 时，求顶点D的坐标

(2)、若OD=OB，求 $m$ 的值；

(3)、设E为A，B两点间抛物线上的一个动点（含端点A，B），过点E作EH⊥ $x$ 轴，垂足为H，交直线BC于点F. 记线段EF的长为t，若t的最大值为 $\frac{9}{2}$ ，求 $m$ 的值.

查看试题解析