河北省2020年中考数学二模试卷
试卷更新日期:2020-07-14 类型:中考模拟
一、单选题
-
1. 下列运算结果为正数的是( )
A、(﹣3)2 B、﹣3÷2 C、0×(﹣2017) D、2﹣32. 世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.00 000 0076克,用科学记数法表示是A、7.6×108克 B、7.6×10-7克 C、7.6×10-8克 D、7.6×10-9克3. 如图所示,能用 , , 三种方法表示同一个角的图形是( )A、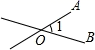 B、
B、 C、
C、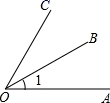 D、
D、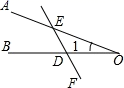 4. 计算: 得( )A、- B、- C、- D、5. 下列图形中,不是中心对称图形的是( )A、
4. 计算: 得( )A、- B、- C、- D、5. 下列图形中,不是中心对称图形的是( )A、 B、
B、 C、
C、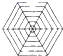 D、
D、 6. 对于 -2,下列说法中正确的是( )A、它是一个无理数 B、它比0小 C、它不能用数轴上的点表示出来 D、它的相反数为 +27. 下列结论中,错误的有:( )
6. 对于 -2,下列说法中正确的是( )A、它是一个无理数 B、它比0小 C、它不能用数轴上的点表示出来 D、它的相反数为 +27. 下列结论中,错误的有:( )①所有的菱形都相似;②放大镜下的图形与原图形不一定相似;
③等边三角形都相似;④有一个角为110度的两个等腰三角形相似;⑤所有的矩形不一定相似.
A、1个 B、2个 C、3个 D、4个8. 如图所示的几何体,它的左视图是( )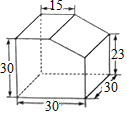 A、
A、 B、
B、 C、
C、 D、
D、 9. 如图,菱形ABCD的对角线AC , BD相交于点O , 过点A作AH⊥BC于点H , 连接OH , 若OB=4,S菱形ABCD=24,则OH的长为( )
9. 如图,菱形ABCD的对角线AC , BD相交于点O , 过点A作AH⊥BC于点H , 连接OH , 若OB=4,S菱形ABCD=24,则OH的长为( )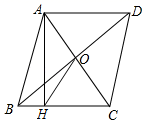 A、3 B、4 C、5 D、610. 在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的大小为( )
A、3 B、4 C、5 D、610. 在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的大小为( )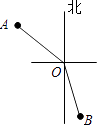 A、69° B、111° C、141° D、159°11. 一个正方形周长与一个等腰三角形的周长相等,若等腰三角形的两边长为 和 ,则这个正方形的对角线长为( )A、 B、 C、 D、12. 下列各式,其中错误的个数有( )A、1个 B、2个 C、3个 D、4个13. 化简 ,其结果为( )A、 B、 C、 D、14. 甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表如图,比较5月份两组家庭用水量的中位数,下列说法正确的是( )
A、69° B、111° C、141° D、159°11. 一个正方形周长与一个等腰三角形的周长相等,若等腰三角形的两边长为 和 ,则这个正方形的对角线长为( )A、 B、 C、 D、12. 下列各式,其中错误的个数有( )A、1个 B、2个 C、3个 D、4个13. 化简 ,其结果为( )A、 B、 C、 D、14. 甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表如图,比较5月份两组家庭用水量的中位数,下列说法正确的是( )甲组12户家庭用水量统计表
用水量(吨)
4
5
6
9
户数
4
5
2
1
 A、甲组比乙组大 B、甲、乙两组相同 C、乙组比甲组大 D、无法判断15. 已知抛物线 与x轴没有交点,则函数 的大致图象是( )A、
A、甲组比乙组大 B、甲、乙两组相同 C、乙组比甲组大 D、无法判断15. 已知抛物线 与x轴没有交点,则函数 的大致图象是( )A、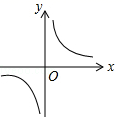 B、
B、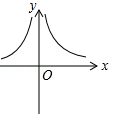 C、
C、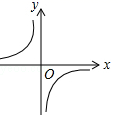 D、
D、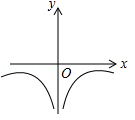 16. 已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示.按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;……在这样连续6次旋转的过程中,点B , M间的距离不可能是( )
16. 已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示.按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;……在这样连续6次旋转的过程中,点B , M间的距离不可能是( )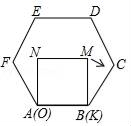 A、0.5 B、0.6 C、0.7 D、0.8
A、0.5 B、0.6 C、0.7 D、0.8二、填空题
-
17. 如图,在四边形ABDC中,E、F、G、H分别为AB、BC、CD、DA的中点,并且E、F、G、H四点不共线.当AC=6,BD=8时,四边形EFGH的周长是 .
 18. 如图,已知线段AB=2,作BD⊥AB , 使BD= AB;连接AD , 以D为圆心,BD长为半径画弧交AD于点E , 以A为圆心,AE长为半径画弧交AB于点C , 则AC长为 .
18. 如图,已知线段AB=2,作BD⊥AB , 使BD= AB;连接AD , 以D为圆心,BD长为半径画弧交AD于点E , 以A为圆心,AE长为半径画弧交AB于点C , 则AC长为 . 19. 如图,抛物线 与直线 的两个交点坐标分别为 , ,则关于x的方程 的解为.
19. 如图,抛物线 与直线 的两个交点坐标分别为 , ,则关于x的方程 的解为.
三、解答题
-
20. 阅读下面材料:点A、B在数轴上分别表示有理数a、b , A、B两点之间的距离表示为AB , 在数轴上A、B两点之间的距离AB=|a﹣b|.回答下列问题:(1)、数轴上表示﹣3和1两点之间的距离是 , 数轴上表示﹣2和3的两点之间的距离是;(2)、数轴上表示x和﹣1的两点之间的距离表示为;(3)、若x表示一个有理数,则|x﹣2|+|x+3|有最小值吗?若有,请求出最小值;若没有,请说明理由.
 21. 某班50名学生参加“迎国庆,手工编织‘中国结’”活动,要求每人编织4~7枚,活动结束后随机抽查了20名学生每人的编织量,并将各类的人数绘制成扇形统计图(如图1)和条形统计图(如图2),
21. 某班50名学生参加“迎国庆,手工编织‘中国结’”活动,要求每人编织4~7枚,活动结束后随机抽查了20名学生每人的编织量,并将各类的人数绘制成扇形统计图(如图1)和条形统计图(如图2),
注:A代表4枚;B代表5枚;C代表6枚;D代表7枚.经确认扇形图是正确的,而条形统计图尚有一处不符合题意.
回答下列问题:
(1)、写出条形图中存在的不符合题意:;(2)、写出这20名学生每人编织‘中国结’数量的众数、中位数、平均数;(3)、求这50名学生中编织‘中国结’个数不少于6的人数;(4)、若从这50名学生中随机选取一名,求其编织‘中国结’个数为C的概率.22. 阅读:已知a、b、c为△ABC的三边长,且满足a2c2﹣b2c2=a4﹣b4 , 试判断△ABC的形状.解:因为a2c2﹣b2c2=a4﹣b4 , ①
所以c2(a2﹣b2)=(a2﹣b2)(a2+b2).②
所以c2=a2+b2 . ③
所以△ABC是直角三角形.④
请据上述解题回答下列问题:
(1)、上述解题过程,从第步(该步的序号)开始出现不符合题意,错的原因为;(2)、请你将正确的解答过程写下来.23. 如图, ,点 为 的中点,点 在线段 上(不与点 重合),将 绕点 顺时针旋转270°后得到大扇形 , 分别与优弧 相切于点 ,且点 在 的异侧. (1)、求证: ;(2)、当 时,求弧 的长.(结果保留π)24. 如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为 ,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
(1)、求证: ;(2)、当 时,求弧 的长.(结果保留π)24. 如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为 ,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
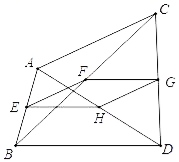
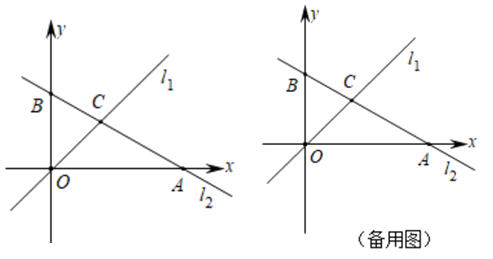 (1)、求点A、点B、点C的坐标,并求出△COB的面积;(2)、若直线l2上存在点P(不与B重合),满足S△COP=S△COB , 请求出点P的坐标;(3)、在y轴右侧有一动直线平行于y轴,分别与l1 , l2交于点M、N,且点M在点N的下方,y轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.25. 如图,在矩形ABCD中,AB=3,BC=4,将对角线AC绕对角线交点O旋转,分别交边AD、BC于点E、F,点P是边DC上的一个动点,且保持DP=AE,连接PE、PF,设AE=x(0<x<3).
(1)、求点A、点B、点C的坐标,并求出△COB的面积;(2)、若直线l2上存在点P(不与B重合),满足S△COP=S△COB , 请求出点P的坐标;(3)、在y轴右侧有一动直线平行于y轴,分别与l1 , l2交于点M、N,且点M在点N的下方,y轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.25. 如图,在矩形ABCD中,AB=3,BC=4,将对角线AC绕对角线交点O旋转,分别交边AD、BC于点E、F,点P是边DC上的一个动点,且保持DP=AE,连接PE、PF,设AE=x(0<x<3).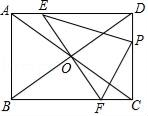 (1)、填空:PC= , FC=(用含x的代数式表示)(2)、求△PEF面积的最小值;(3)、在运动过程中,PE⊥PF是否成立?若成立,求出x的值;若不成立,请说明理由.26. 春节临近,由于我市城区执行严禁燃放烟花炮竹令,某商店发现了商机经销一种安全、无污染的电子鞭炮已知这种电子鞭炮的成本价每盒80元,市场调查发现春节期间,该种电子鞭炮每天的销售量y(盒)与销售单价x(元)有如下关系:y=﹣2x+320(80≤x≤160).设这种电子鞭炮每天的销售利润为w元.(1)、求w与x的函数关系式;(2)、该种电子鞭炮的销售单价定为多少元时,每天销售利润最大?最大利润是多少元?(3)、若该商店销售这种电子鞭炮要想每天获得销售利润2400元,应如何定价?
(1)、填空:PC= , FC=(用含x的代数式表示)(2)、求△PEF面积的最小值;(3)、在运动过程中,PE⊥PF是否成立?若成立,求出x的值;若不成立,请说明理由.26. 春节临近,由于我市城区执行严禁燃放烟花炮竹令,某商店发现了商机经销一种安全、无污染的电子鞭炮已知这种电子鞭炮的成本价每盒80元,市场调查发现春节期间,该种电子鞭炮每天的销售量y(盒)与销售单价x(元)有如下关系:y=﹣2x+320(80≤x≤160).设这种电子鞭炮每天的销售利润为w元.(1)、求w与x的函数关系式;(2)、该种电子鞭炮的销售单价定为多少元时,每天销售利润最大?最大利润是多少元?(3)、若该商店销售这种电子鞭炮要想每天获得销售利润2400元,应如何定价?