河北省唐山市开平区2020年中考数学一模试卷
试卷更新日期:2020-07-14 类型:中考模拟
一、单选题
-
1. 下列图形中,只有一条对称轴的是( )A、等腰三角形
 B、菱形
B、菱形  C、正五边形
C、正五边形  D、矩形
D、矩形  2. 如图是某手机用户微信支付情况, 月 日显示 的意思( )
2. 如图是某手机用户微信支付情况, 月 日显示 的意思( ) A、转出了 元 B、收入了 元 C、转入 元 D、抢了 元红包3. 已知三角形的三边长为 , , .如果 是整数,则 的值不可能是( )A、 B、 C、 D、4. 一辆匀速行驶的汽车在 点 分的时候距离某地 ,若汽车需要在 点以前经过某地,设汽车在这段路上的速度为 ( 小时),列式表示正确的是( )A、 B、 C、 D、5. 如图四边形 是菱形, ,则 ( )
A、转出了 元 B、收入了 元 C、转入 元 D、抢了 元红包3. 已知三角形的三边长为 , , .如果 是整数,则 的值不可能是( )A、 B、 C、 D、4. 一辆匀速行驶的汽车在 点 分的时候距离某地 ,若汽车需要在 点以前经过某地,设汽车在这段路上的速度为 ( 小时),列式表示正确的是( )A、 B、 C、 D、5. 如图四边形 是菱形, ,则 ( )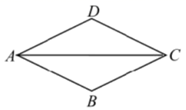 A、 B、 C、 D、6. 三位同学在计算: ,用了不同的方法,
A、 B、 C、 D、6. 三位同学在计算: ,用了不同的方法,小小说: 的 , 和 分别是 , 和 ,所以结果应该是 ;
聪聪说:先计算括号里面的数, ,再乘以 得到 ;
明明说:利用分配律,把 与 , 和 分别相乘得到结果是-
对于三个同学的计算方式,下面描述正确的是( )
A、三个同学都用了运算律 B、聪聪使用了加法结合律 C、明明使用了分配律 D、小小使用了乘法交换律7. 去年年末,武汉市发生新型冠状病毒引起的传染病,这种病毒非常的小,直径约为 (纳米), ,则 新冠病毒直径大小用科学记数法表示为( )A、 B、 C、 D、8. 如图,直线 和直线 被直线 所截,且 , ,则 ,下面推理过程错误的是( )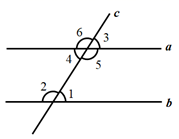 A、 ,又 (邻补角定义), B、 ,又 (邻补角定义), C、 又 (邻补角定义), D、 ,∵∠3+∠4=180°(邻补角定义)9. 如图,正五边形 绕点 旋转了 ,当 时,则 ( )
A、 ,又 (邻补角定义), B、 ,又 (邻补角定义), C、 又 (邻补角定义), D、 ,∵∠3+∠4=180°(邻补角定义)9. 如图,正五边形 绕点 旋转了 ,当 时,则 ( ) A、 B、 C、 D、10. 小王和小李两名同学研究本班女同学的身高情况,两人分别统计了一组数据,
A、 B、 C、 D、10. 小王和小李两名同学研究本班女同学的身高情况,两人分别统计了一组数据,小王
小李
经过计算得到两组数据的方差,小王一组的方差为 ,小李一组的方差为 ;则下列说法正确的是( )
A、小王统计的一组数据比较稳定 B、小李统计的一组数据比较稳定 C、两组数据一样稳定 D、不能比较稳定性11. 某地为了促进旅游业的发展,要在如图所示的三条公路 , , 围成的一块地上修建一个度假村,要使这个度假村到 , 两条公路的距离相等,且到 , 两地的距离相等,下列选址方法绘图描述正确的是( ) A、画 的平分线,再画线段 的垂直平分线,两线的交点符合选址条件 B、先画 和 的平分线,再画线段 的垂直平分线,三线的交点符合选址条件 C、画三个角 , 和 三个角的平分线,交点即为所求 D、画 , , 三条线段的垂直平分线,交点即为所求12. 如图,数轴上 , , , , 五个点表示连续的五个整数 , , , , ,且 ,则下列说法正确的有( )
A、画 的平分线,再画线段 的垂直平分线,两线的交点符合选址条件 B、先画 和 的平分线,再画线段 的垂直平分线,三线的交点符合选址条件 C、画三个角 , 和 三个角的平分线,交点即为所求 D、画 , , 三条线段的垂直平分线,交点即为所求12. 如图,数轴上 , , , , 五个点表示连续的五个整数 , , , , ,且 ,则下列说法正确的有( )①点 表示的数字是
②
③
④
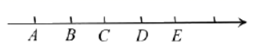 A、都之前 B、只有①③正确 C、只有①②③正确 D、只有③错误13. 使分式 和分式 相等的x值是( )A、 B、 C、 D、14. 一透明的敞口正方体容器 装有一些液体,棱 始终在水平桌面上,容器底部的倾斜角为 ( ,如图1所示).如图1,液面刚好过棱 ,并与棱 交于点 ,此时液体的形状为直三棱柱,其三视图及尺寸如图2所示.则此时 的长为( )
A、都之前 B、只有①③正确 C、只有①②③正确 D、只有③错误13. 使分式 和分式 相等的x值是( )A、 B、 C、 D、14. 一透明的敞口正方体容器 装有一些液体,棱 始终在水平桌面上,容器底部的倾斜角为 ( ,如图1所示).如图1,液面刚好过棱 ,并与棱 交于点 ,此时液体的形状为直三棱柱,其三视图及尺寸如图2所示.则此时 的长为( ) A、 B、 C、 D、15. 如图所示的直角坐标系内,双曲线的解析式为 ,若将原坐标系的 轴向上平移两个单位,则双曲线 在新坐标系内的解析式为( )
A、 B、 C、 D、15. 如图所示的直角坐标系内,双曲线的解析式为 ,若将原坐标系的 轴向上平移两个单位,则双曲线 在新坐标系内的解析式为( ) A、 B、 C、 D、16. 课外小组的同学们,在校内准备测量墙外一手机发射塔的高度,小组的同学们首先在校内宽敞处选定一点 ,在 点测得到塔顶 的仰角为 ,然后他们沿与 和塔底 连线 垂直的方向走了 米到达 点,在 点观测塔顶 的仰角为 ,小组根据这些数据计算出发射塔的高度最接近的数值是( )
A、 B、 C、 D、16. 课外小组的同学们,在校内准备测量墙外一手机发射塔的高度,小组的同学们首先在校内宽敞处选定一点 ,在 点测得到塔顶 的仰角为 ,然后他们沿与 和塔底 连线 垂直的方向走了 米到达 点,在 点观测塔顶 的仰角为 ,小组根据这些数据计算出发射塔的高度最接近的数值是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
17. 当 且 时,如果 ,则n= .18. 在实数范围定义一种新运算 (加减乘除是普通的运算),例如: ,计算 , 若 ,则 .19. 有一边长为 的等边 游乐场,某人从边 中点 出发,先由点 沿平行于 的方向运动到 边上的点 ,再由 沿平行于 方向运动到 边上的点 ,又由点 沿平行于 方向运动到 边上的点 ,则此人至少要运动 ,才能回到点 .如果此人从 边上意一点出发,按照上面的规律运动,则此人至少走 ,就能回到起点.
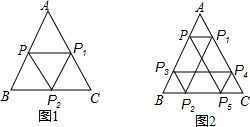
三、解答题
-
20. 小盛和丽丽在学完了有理数后做起了数学游戏(1)、规定用四个不重复(绝对值小于 )的正整数通过加法运算后结果等于
小盛: ;丽丽: ,问是否还有其他的算式,如果有请写出来一个,如果没有,请简单说明理由;
(2)、规定用四个不重复(绝对值小 )的整数通过加法运算后结果等小盛: ;丽丽: ;请根据要求再写出一个与他们不同的算式.
(3)、用(2)中小盛和丽丽的算式继续排列下去组成一个数列,使相邻的四个数的和都等于 ,小盛: , , , ,丽丽: , , , ,
则 ; . 求丽丽写出的数列的前 项的和.
21. 在一个不透明的口袋中放入 个大小形状几乎完全相同实验用的鸡蛋,鸡蛋的质量有微小的差距(用手感觉不到差异),质量分别为 、 、 克,已知随机的摸出一个鸡蛋,摸到 克和 克的鸡蛋的概率是相等的.(1)、求这四个鸡蛋质量的众数和中位数(2)、小明做实验需要拿走一个鸡蛋,芳芳在小明拿走后从剩下的三个鸡蛋中随机的拿走一个①通过计算分析小明拿走一个鸡蛋后,剩下的三个鸡蛋质量的中位数是多少?
②假设小明拿走的鸡蛋质量为 克,芳芳随机的拿出一个鸡蛋后又放回,之后再随机的拿出一个鸡蛋,请用树状图求芳芳两次拿到都是 克的鸡蛋的概率?
22. 完全平方公式是初中数学的重要公式之一: ,完全平方公式既可以用来进行整式计算又可以用来进行分解因式,在学习中芳芳同学发现 也可以用完全平方公式进行分解因式, ;根据以上发现解决问题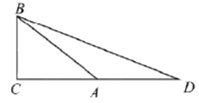 (1)、写出一个上面相同的式子,并进行分解因式;(2)、若 ,请用 , 表示 ,(3)、如图在 中, , , ,延长 至点 ,使 ,求 的长(参考上面提供的方法把结果进行化简)23. 有甲,乙两个电子团队整理一批电脑数据,整理电脑的台数为 (台)与整理需要的时间 之间关系如下图所示,请依据图象提供的信息解答下列问题:
(1)、写出一个上面相同的式子,并进行分解因式;(2)、若 ,请用 , 表示 ,(3)、如图在 中, , , ,延长 至点 ,使 ,求 的长(参考上面提供的方法把结果进行化简)23. 有甲,乙两个电子团队整理一批电脑数据,整理电脑的台数为 (台)与整理需要的时间 之间关系如下图所示,请依据图象提供的信息解答下列问题: (1)、乙队工作 小时整理台电脑,工作 时两队一共整理了台;(2)、求甲、乙两队 与 的关系式.(3)、甲、乙两队整理电脑台数相等时,直接写出 的值.24. 如图, 中, , ,将 绕点 按逆时针方向旋转 .得到 ,连接 , 交于点 .
(1)、乙队工作 小时整理台电脑,工作 时两队一共整理了台;(2)、求甲、乙两队 与 的关系式.(3)、甲、乙两队整理电脑台数相等时,直接写出 的值.24. 如图, 中, , ,将 绕点 按逆时针方向旋转 .得到 ,连接 , 交于点 .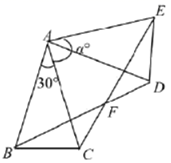 (1)、求证: ;(2)、用 表示 的度数;(3)、若使四边形 是菱形,求 的度数,25. 已知,如图,二次函数 (其中 , 是常数, 为正整数)
(1)、求证: ;(2)、用 表示 的度数;(3)、若使四边形 是菱形,求 的度数,25. 已知,如图,二次函数 (其中 , 是常数, 为正整数) (1)、若 经过点 求 的值.(2)、当 ,若 与 轴有公共点时且公共点的横坐标为非零的整数,确定 的值;(3)、在(2)的条件下将 的图象向下平移 个单位,得到函数图象 ,求 的解析式;(4)、在(3)的条件下,将 的图象在 轴下方的部分沿 轴翻折,图象的其余部分保持不变,得到一个新的图象 ,请结合新的图象解答问题,若直线 与 有两个公共点时,请直接写出 的取值范围.26. 如图,点 在矩形 的边 上, , ,连接 ,线段 绕点 旋转 ,得到线段 ,以线段 为直径做 .
(1)、若 经过点 求 的值.(2)、当 ,若 与 轴有公共点时且公共点的横坐标为非零的整数,确定 的值;(3)、在(2)的条件下将 的图象向下平移 个单位,得到函数图象 ,求 的解析式;(4)、在(3)的条件下,将 的图象在 轴下方的部分沿 轴翻折,图象的其余部分保持不变,得到一个新的图象 ,请结合新的图象解答问题,若直线 与 有两个公共点时,请直接写出 的取值范围.26. 如图,点 在矩形 的边 上, , ,连接 ,线段 绕点 旋转 ,得到线段 ,以线段 为直径做 .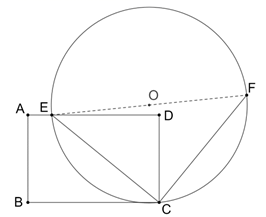
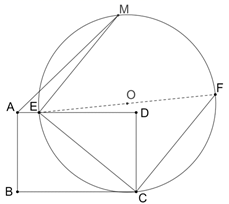 (1)、请说明点 一定在 上的理由,(2)、①点 在 上, 为 的直径,求证:点 到 的距离等于线段 的长.
(1)、请说明点 一定在 上的理由,(2)、①点 在 上, 为 的直径,求证:点 到 的距离等于线段 的长.②当 面积取得最大值时,求 半径的长.
(3)、当 与矩形 的边相切时,计算扇形 的面积.