2020年暑期衔接训练青岛版数学八年级下册：第8讲勾股定理的逆定理

试卷更新日期：2020-07-14 类型：复习试卷

进入出卷网下载

一、单选题

1. 以下列各组数为边的三角形中，是直角三角形的有（）
（ 1 ）3，4，5；（2） $\sqrt{3}$ ， $\sqrt{4}$ ， $\sqrt{5}$ ；（3） $3^{2}$ ， $4^{2}$ ， $5^{2}$ ；（4）0.03，0.04，0.05.

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列说法不能得到直角三角形的（）

A、三个角度之比为 1：2：3 的三角形 B、三个边长之比为 3：4：5 的三角形 C、三个边长之比为 8：16：17 的三角形 D、三个角度之比为 1：1：2 的三角形

查看试题解析
3. 将直角三角形的各边都缩小或扩大同样的倍数后，得到的三角形是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、不确定

查看试题解析
4. 下列三角形中，不是直角三角形的是（）

A、△ABC中,∠A=∠B-∠C B、△ABC中,a:b:c=1:2:3 C、△ABC中,a²=c²-b² D、△ABC中,三边的长分别为m²+n²,m²-n²,2mn(m>n>0)

查看试题解析
5. $△ A B C$ 的三边 $B C = a, A C = b, A B = c$ ，且 $(a + c) (a - c) - b^{2} = 0$ ，下列结论正确的是（）

A、 $△ A B C$ 是等腰直角三角形且 $∠ C = 90 °$ B、 $△ A B C$ 是直角三角形或等腰三角形 C、 $△ A B C$ 是直角三角形，且 $∠ C = 90 °$ D、 $△ A B C$ 是直角三角形，且 $∠ A = 90 °$

查看试题解析
6. 有下面的判断：
①若△ABC中，a²＋b²≠c² ，则△ABC不是直角三角形；②△ABC是直角三角形，∠C=90°，则a²＋b²=c²；③若△ABC中，a²－b²=c² ，则△ABC是直角三角形；④若△ABC是直角三角形，则(a＋b)(a－b)=c².其中判断正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
7. 有六根细木棒，它们的长度分别是2，4，6，8，10，12（单位：cm），从中取出三根首尾顺次连接搭成一个直角三角形，则这三根木棒的长度分别为（）

A、2，4，8 B、4，8，10 C、6，8，10 D、8，10，12

查看试题解析
8. 已知a、b、c是三角形的三边长，如果满足（a﹣6）²+ $\sqrt{b - 8}$ +|c﹣10|=0，则三角形的形状是（）

A、直角三角形 B、等边三角形 C、钝角三角形 D、底与腰不相等的等腰三角形

查看试题解析
9. 已知：△ABC中，AB=4，AC=3，BC= $\sqrt{7}$ ，则△ABC的面积是（　　）

A、6 B、5 C、 $\frac{3 \sqrt{7}}{2}$ D、2 $\sqrt{7}$

查看试题解析
10. 下列命题：
①如果a、b、c为一组勾股数，那么4a、4b、4c仍是勾股数；
②如果直角三角形的两边是3，4，那么斜边必是5；
③如果一个三角形的三边是12，25，21，那么此三角形必是直角三角形；
④一个等腰直角三角形的三边是a、b、c，（a＞b=c），那么a²：b²：c²=2：1：1．
其中正确的是（　　）

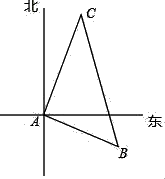
A、①② B、①③ C、①④ D、②④

查看试题解析
11.
一艘轮船和一艘渔船同时沿各自的航向从港口O出发，如图所示，轮船从港口O沿北偏西20°的方向行60海里到达点M处，同一时刻渔船已航行到与港口O相距80海里的点N处，若M、N两点相距100海里，则∠NOF的度数为（　　）

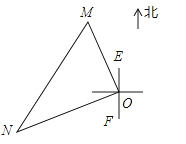A、50° B、60° C、70° D、80°

查看试题解析
12. 已知：在△ABC中，a、b、c分别为∠A、∠B、∠C的对边，则下列条件中：
①a=3，b=4，c= $\sqrt{7}$ ；
②a²：b²：c²=6：8：10；
③∠A：∠B：∠C=3：4：5；
④∠A=2∠B，∠C=3∠B．
其中能判断△ABC是直角三角形的条件为（）

A、①② B、①④ C、②④ D、②③

查看试题解析

二、填空题

13. 已知三角形的三边长分别为 $\sqrt{6}$ ， $\sqrt{6}$ ， $2 \sqrt{3}$ ，则此三角形的最长边上的高等于。

查看试题解析
14. 分别以△ABC的各边为一边向三角形外部作正方形，若这三个正方形的面积分别为6cm²、8cm²、10cm² ，则△ABC直角三角形.（填“是”或“不是”）

查看试题解析
15. 用长度相同的火柴棒首尾相连摆直角三角形，你认为至少要用根才能摆成．

查看试题解析
16. 有一根长24cm的小木棒，把它分成三段，组成一个直角三角形，且每段的长度都是偶数，则三段小木棒的长度分别是 cm， cm， cm．

查看试题解析
17. 某花园小区有一空地（如图所示的△ABC），为美化小区，居委会准备将其开发种植花草，经测量AB=13m，BC=10m，BC边上的中线AD=12m，如果种植每平方米花草需要50元，那么种植这块三角形空地需要元．

查看试题解析
18. 探索勾股数的规律：
观察下列各组数：（3，4，5），（5，12，13），（7，24，25），（9，40，41）…可发现，4= $\frac{3^{2} - 1}{2}$ ，12= $\frac{5^{2} - 1}{2}$ ，24= $\frac{7^{2} - 1}{2}$ …请写出第5个数组：．

查看试题解析
19. 如图，在四边形ABCD中，对角线AC、BD相交于点E，∠CBD=90°，BC=4，BE=ED=3，AC=10，则四边形ABCD的面积为．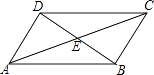

查看试题解析
20. 如图所示，在△ABC中，AB：BC：CA=3：4：5，且周长为36cm，点P从点A开始沿AB边向B点以每秒1cm的速度移动；点Q从点B沿BC边向点C以每秒2cm的速度移动，如果同时出发，则过3秒时，△BPQ的面积为 cm² ．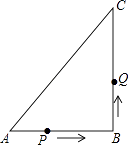

查看试题解析

三、作图题

21. 如图，正方形网格中，每个小正方形的边长均为1，每个小正方形的顶点叫格点．

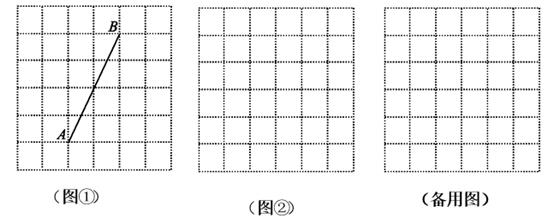(1)、在图①中，求线段AB的长度；若在图中画出以C为直角顶点的Rt△ABC ，使点C在格点上，请在图中画出所有点C；

(2)、在图②中，以格点为顶点，请先用无刻度的直尺画正方形ABCD ，使它的面积为13；再画一条直线PQ（不与正方形对角线重合），使PQ恰好将正方形ABCD的面积二等分(保留作图痕迹）.

查看试题解析

四、解答题

22. 在△ABC中，三条边长分别为a、b、c，且a=n， $b = \frac{n^{2}}{4} - 1, c = \frac{n^{2}}{4} + 1$ (n是大于2的偶数)，求证: △ABC是直角三角形.

查看试题解析
23. 如图是一块地的平面图，AD＝4 m，CD＝3 m，AB＝13 m，BC＝12 m，∠ADC＝90°，求这块地的面积．

查看试题解析
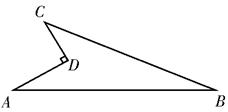24. 一个零件的形状如图，按规定这个零件的∠A与∠BDC都要是直角，工人师傅量得零件各边尺寸：AD=4，AB=3，DC=12，BC=13，BD=5．这个零件符合要求吗？

查看试题解析
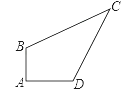25. 如果ΔABC的三边分别为a、b、c，且满足a²+b²+c²+50=6a+8b+10c，判断ΔABC的形状。

查看试题解析
26. 如图，在△ABC中，∠ABC=90°，AB=6cm，AD=24cm，BC与CD的长度之和为34cm，其中C是直线l上的一个动点，请你探究当C离点B有多远时，△ACD是以DC为斜边的直角三角形．

查看试题解析
27. 如图，有一艘货船和一艘客船同时从港口A出发，客船每小时比货船多走5海里，客船与货船速度的比为4：3，货船沿东偏南10°方向航行，2小时后货船到达B处，客船到达C处，若此时两船相距50海里.

(1)、求两船的速度分别是多少？

(2)、求客船航行的方向.

查看试题解析
28. 阅读：能够成为直角三角形的三边长的三个正整数a，b，c，称为勾股数．世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》，其勾股数组的公式为 ${\begin{matrix} \begin{array}{l} a = \frac{1}{2} (m^{2} - n^{2}) \\ b = m n \end{array} \\ c = \frac{1}{2} (m^{2} + n^{2}) \end{matrix}$ 其中m＞n＞0，m，n是互质的奇数．
应用：当n＝1时，求有一边长为5的直角三角形的另外两条边的长．

查看试题解析

2020年暑期衔接训练青岛版数学八年级下册：第8讲 勾股定理的逆定理

一、单选题

二、填空题

三、作图题

四、解答题

2020年暑期衔接训练青岛版数学八年级下册：第8讲勾股定理的逆定理