河北省唐山市丰润区2020年中考数学一模试卷
试卷更新日期:2020-07-14 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、 B、 C、5 D、-52. 若 ,则 的余角等于( )A、 B、 C、 D、3. 使得式子 有意义的x的取值范围是( )A、x≥4 B、x>4 C、x≤4 D、x<44. 已知正多边形的一个外角为36°,则该正多边形的边数为( ).A、12 B、10 C、8 D、65. 下列运算正确的是( )A、 B、 C、 D、6. 如图是由四个相同的小正方体组成的立体图形,它的俯视图为( )
 A、
A、 B、
B、 C、
C、 D、
D、 7. 用科学记数法表示的数 ,原来是( )A、 B、 C、 D、8. 化简: ( )A、 B、 C、 D、9. 如图,直线 ,点A在直线 上,以点A为圆心,适当长度为半径画弧,分别交直线 、 于B、C两点,连结AC、BC.若 ,则 的大小为( )
7. 用科学记数法表示的数 ,原来是( )A、 B、 C、 D、8. 化简: ( )A、 B、 C、 D、9. 如图,直线 ,点A在直线 上,以点A为圆心,适当长度为半径画弧,分别交直线 、 于B、C两点,连结AC、BC.若 ,则 的大小为( )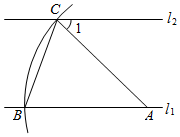 A、 B、 C、 D、10. 甲、乙二人做某种机械零件,已知每小时甲比乙少做8个,甲做120个所用的时间与乙做150个所用的时间相等,设甲每小时做x个零件,下列方程正确的是( )A、 B、 C、 D、11. 如图,在 中,将 沿AC折叠后,点D恰好落在DC的延长线上的点E处.若 , ,则 的周长为( )
A、 B、 C、 D、10. 甲、乙二人做某种机械零件,已知每小时甲比乙少做8个,甲做120个所用的时间与乙做150个所用的时间相等,设甲每小时做x个零件,下列方程正确的是( )A、 B、 C、 D、11. 如图,在 中,将 沿AC折叠后,点D恰好落在DC的延长线上的点E处.若 , ,则 的周长为( )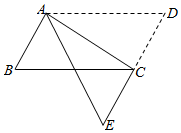 A、12 B、15 C、18 D、2112. 如图, 内接于圆 , , ,若 ,则弧 的长为( )
A、12 B、15 C、18 D、2112. 如图, 内接于圆 , , ,若 ,则弧 的长为( )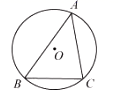 A、 B、 C、 D、13. 小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为( )
A、 B、 C、 D、13. 小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为( )
 A、 B、 C、 D、14. 如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )
A、 B、 C、 D、14. 如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )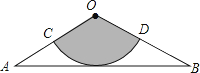 A、10cm B、15cm C、10 cm D、20 cm15. 定义新运算: ,例如: , ,则 的图像是( )A、
A、10cm B、15cm C、10 cm D、20 cm15. 定义新运算: ,例如: , ,则 的图像是( )A、 B、
B、 C、
C、 D、
D、 16. 如图, 的斜边在 轴上, ,含 角的顶点与原点重合,直角顶点 在第二象限,将 绕原点顺时针旋转 后得到 ,则 点的对应点 的坐标是( )
16. 如图, 的斜边在 轴上, ,含 角的顶点与原点重合,直角顶点 在第二象限,将 绕原点顺时针旋转 后得到 ,则 点的对应点 的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
17. 如图,数轴上A、B两点所表示的数分别是-4和2, 点C是线段AB的中点,则点C所表示的数是.
 18. 如图,在平面直角坐标系中,已知 经过原点 ,与 轴、 轴分别交于 、 两点,点 坐标为 , 与 交于点 , ,则圆中阴影部分的面积为.
18. 如图,在平面直角坐标系中,已知 经过原点 ,与 轴、 轴分别交于 、 两点,点 坐标为 , 与 交于点 , ,则圆中阴影部分的面积为. 19. 如图,在平面直角坐标系中,函数 和 的图象分别为直线 ,过 上的点A1(1, )作x轴的垂线交 于点A2 , 过点A2作y轴的垂线交 于点A3 , 过点A3作x轴的垂线交 于点A4…,一次进行下去,则点 的横坐标为 .
19. 如图,在平面直角坐标系中,函数 和 的图象分别为直线 ,过 上的点A1(1, )作x轴的垂线交 于点A2 , 过点A2作y轴的垂线交 于点A3 , 过点A3作x轴的垂线交 于点A4…,一次进行下去,则点 的横坐标为 .
三、解答题
-
20. 计算:(1)、(2)、分解因式: + (2x-5)21. 如图,菱形 中,作 、 ,分别交 、 的延长线于点 .
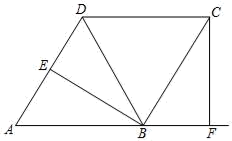 (1)、求证: ;(2)、若点 恰好是 的中点, ,求 的值.22. 高尔基说:“书,是人类进步的阶梯.”阅读可以丰富知识、拓展视野、充实生活等诸多益处.为了解学生的课外阅读情况,某校随机抽查了部分学生阅读课外书册数的情况,并绘制出如下统计图.其中条形统计图因为破损丢失了阅读5册书数的数据.
(1)、求证: ;(2)、若点 恰好是 的中点, ,求 的值.22. 高尔基说:“书,是人类进步的阶梯.”阅读可以丰富知识、拓展视野、充实生活等诸多益处.为了解学生的课外阅读情况,某校随机抽查了部分学生阅读课外书册数的情况,并绘制出如下统计图.其中条形统计图因为破损丢失了阅读5册书数的数据.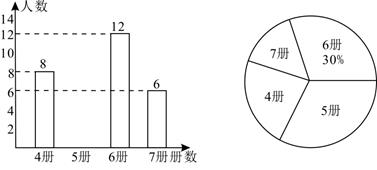 (1)、求条形图中丢失的数据,并写出阅读书册数的众数和中位数;(2)、根据随机抽查的这个结果,请估计该校1200名学生中课外阅读5册书的学生人数;(3)、若学校又补查了部分同学的课外阅读情况,得知这部分同学中课外阅读最少的是6册,将补查的情况与之前的数据合并后发现中位数并没有改变,试求最多补查了多少人?23. 在一次海上救援中,两艘专业救助船 同时收到某事故渔船的求救讯息,已知此时救助船 在 的正北方向,事故渔船 在救助船 的北偏西30°方向上,在救助船 的西南方向上,且事故渔船 与救助船 相距120海里.
(1)、求条形图中丢失的数据,并写出阅读书册数的众数和中位数;(2)、根据随机抽查的这个结果,请估计该校1200名学生中课外阅读5册书的学生人数;(3)、若学校又补查了部分同学的课外阅读情况,得知这部分同学中课外阅读最少的是6册,将补查的情况与之前的数据合并后发现中位数并没有改变,试求最多补查了多少人?23. 在一次海上救援中,两艘专业救助船 同时收到某事故渔船的求救讯息,已知此时救助船 在 的正北方向,事故渔船 在救助船 的北偏西30°方向上,在救助船 的西南方向上,且事故渔船 与救助船 相距120海里.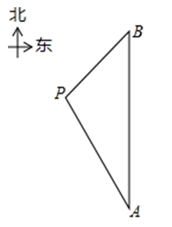 (1)、求收到求救讯息时事故渔船 与救助船 之间的距离;(2)、若救助船A , 分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船 处搜救,试通过计算判断哪艘船先到达.24. 双曲线 (k为常数,且 )与直线 交于 两点.
(1)、求收到求救讯息时事故渔船 与救助船 之间的距离;(2)、若救助船A , 分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船 处搜救,试通过计算判断哪艘船先到达.24. 双曲线 (k为常数,且 )与直线 交于 两点.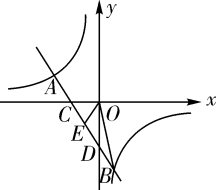 (1)、求k与b的值;(2)、如图,直线AB交x轴于点C,交y轴于点D,若点E为CD的中点,求△BOE的面积.25. 如图, 为 直径, 点为半径 上异于 点和 点的一个点,过 点作与直径 垂直的弦 ,连接 ,作 , 交 于 点,连接 、 , 交 于 点.
(1)、求k与b的值;(2)、如图,直线AB交x轴于点C,交y轴于点D,若点E为CD的中点,求△BOE的面积.25. 如图, 为 直径, 点为半径 上异于 点和 点的一个点,过 点作与直径 垂直的弦 ,连接 ,作 , 交 于 点,连接 、 , 交 于 点. (1)、求证: 为 的切线;(2)、若 的半径为 , ,求 ;(3)、请猜想 与 的数量关系,并加以证明.26. 如图①,在平面直角坐标系中,直线 与 轴交于点 ,与 轴交于点 ;抛物线 过 , 两点,与 轴交于另一点 ,抛物线的顶点为 .
(1)、求证: 为 的切线;(2)、若 的半径为 , ,求 ;(3)、请猜想 与 的数量关系,并加以证明.26. 如图①,在平面直角坐标系中,直线 与 轴交于点 ,与 轴交于点 ;抛物线 过 , 两点,与 轴交于另一点 ,抛物线的顶点为 . (1)、求抛物线的解析式;(2)、在直线 上方的抛物线上有一动点 ,求出点 到直线 的距离的最大值;(3)、如图②,直线 与抛物线的对称轴相交于点 ,请直接写出 的平分线与 轴的交点 的坐标.
(1)、求抛物线的解析式;(2)、在直线 上方的抛物线上有一动点 ,求出点 到直线 的距离的最大值;(3)、如图②,直线 与抛物线的对称轴相交于点 ,请直接写出 的平分线与 轴的交点 的坐标.