河北省石家庄市2020年中考数学一模试卷

试卷更新日期：2020-07-14 类型：中考模拟

进入出卷网下载

一、单选题

1. 古人使用下面的几何图形研究勾股定理，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 中国政府在2020年3月7日，向世界卫生组织捐款2000万美元，支持世卫组织开展抗击新冠肺炎疫情国际合作.2000万用科学记数法表示为 $2 \times 10^{n} ， n$ 的值为（）

A、5 B、6 C、7 D、8

查看试题解析
3. 下列计算正确的是（）

A、 $| - 2 | = - 2$ B、 ${(\frac{1}{3})}^{2} = \frac{1}{6}$ C、 ${(- 3)}^{0} = 0$ D、 $2^{- 1} = \frac{1}{2}$

查看试题解析
4. 如图， $A B$ 是河堤横断面的迎水坡，堤高 $A C = \sqrt{3}$ ，水平距离 $B C = 1$ ，则斜坡 $A B$ 的坡度为（）

A、 $\sqrt{3}$ B、 $\frac{\sqrt{3}}{3}$ C、 $30^{\circ}$ D、 $60^{\circ}$

查看试题解析
5. 如果 $a > b ， c < 1$ ，那么下列不等式一定成立的是（）

A、 $a c > b c$ B、 $a + c > b$ C、 $a c < b c$ D、 $a - c > b - c$

查看试题解析
6. 在底面为正三角形，且底面周长为 $9$ 的直棱柱上，截去一个底面为正三角形，且底面周长为 $3$ 的直棱柱后(如图所示)，所得几何体的俯视图的周长为（）

A、 $6$ B、 $7$ C、 $7.5$ D、 $8$

查看试题解析
7. 为了解某校九年级学生跳远成绩的情况，随机抽取 $30$ 名学生的跳远成绩(满分 $10$ 分).绘制成下表：

成绩/分

$5$

$6$

$7$

$8$

$9$

$10$

人数/人

$x$

$y$

$6$

$8$

$5$

$4$

关于跳远成绩的统计量中，一定不随 $x ， y$ 的变化而变化的是（）

A、众数，中位数 B、中位数，方差 C、平均数，方差 D、平均数，众数

查看试题解析
8. 为防止森林火灾的发生，会在森林中设置多个观测点.如图.若起火点 $M$ 在观测台 $B$ 的南偏东 $46^{\circ}$ 的方向上.点 $A$ 表示另一处观测台，若 $A M ⊥ B M ，$ 那么起火点 $M$ 在观测台 $A$ 的（）

A、南偏东 $44^{\circ}$ B、南偏西 $44^{\circ}$ C、北偏东 $46^{\circ}$ D、北偏西 $46^{\circ}$

查看试题解析
9. 已知三个数 $- π$ ，-3， $- 2 \sqrt{2}$ ，它们的大小关系是（）

A、 $- π < - 2 \sqrt{2} < - 3$ B、 $- 3 < - π < - 2 \sqrt{2}$ C、 $- 2 \sqrt{2} < - π < - 3$ D、 $- π < - 3 < - 2 \sqrt{2}$

查看试题解析
10. 如图，以正五边形 $A B C D E$ 的对角线 $B E$ 为边，作正方形 $B E F G ，$ 使点 $A$ 落在正方形 $B E F G$ 内，则 $∠ A B G$ 的度数为（）

A、 $18^{\circ}$ B、 $36^{\circ}$ C、 $54^{\circ}$ D、 $72^{\circ}$

查看试题解析
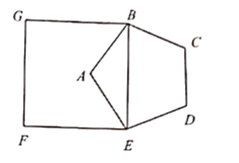11. 关于 $x$ 的方程 $x^{2} - m x + \frac{m}{2} - \frac{1}{4} = 0$ 有两个相等的实数根.则反比例函数 $y = \frac{m}{x} (x > 0)$ 的图象在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
12. 如图，在平面直角坐标系中，以 $O$ 为圆心，适当长为半径画弧，交 $x$ 轴于点 $A ，$ 交 $y$ 轴于点 $B ，$ 再分别以点 $A ， B$ 为圆心，大于 $\frac{1}{2} A B$ 的长为半径画弧，两弧交于点 $P$ .若点 $P$ 的坐标为 $(\frac{1}{a - 1} ， \frac{2}{a}) ，$ 则 $a$ 的值为（）

A、 $\frac{1}{2}$ B、 $2$ C、 $1$ D、 $- 1$

查看试题解析
13. 现有两种礼包，甲种礼包里面含有 $4$ 个毛绒玩具和 $1$ 套文具.乙种礼包里面含有 $3$ 个毛绒玩具和 $2$ 套文具.现在需要 $37$ 个毛绒玩具， $18$ 套文具，则需要采购甲种礼包的数量为（）

A、 $2$ 件 B、 $3$ 件 C、 $4$ 件 D、 $5$ 件

查看试题解析
14. 如图，有一块形状为 $R t △ A R C$ 的铁板余料，已知 $∠ A = 90 ° ， A B = 6 c m ， A C = 8 c m .$ 要把它加工成一个形状为 $▱ D E F G$ 的工件，使 $G F$ 在 $B C$ 上， $D ， E$ 两点分别在 $A B ， A C$ 上，且 $D E = 5 c m$ ，则 $▱ D E F G$ 的面积为（）

A、 $24 c m^{2}$ B、 $12 c m^{2}$ C、 $9 c m^{2}$ D、 $6 c m^{2}$

查看试题解析
15. 如图，直线 $l_{1} ： y = 2 x + 2$ 交 $x$ 轴、 $y$ 轴于 $A ， C$ 两点，直线 $l_{2} ： y = - \frac{1}{2} x + 2$ 交 $x$ 轴、 $y$ 轴于 $B ， C$ 两点，点 $P (m ， 1)$ 是 $△ A B C$ 内部(包括边界)的一点，则 $m$ 可能是（）

A、 $3$ B、 $- 1 \frac{1}{2}$ C、 $0 \leq m \leq 2$ D、 $- 1 \leq m \leq 4$

查看试题解析
16. 如图，以点 $O$ 为圆心， $4$ 为半径作扇形 $A O B ，$ 已知： $A O ⊥ B O ，$ 点 $E$ 在 $O A$ 上，且 $0 E = 2 \sqrt{3} ， C D$ 垂直平分 $O B ，$ 动点 $P$ 在线段 $C D$ 上运动(不与点 $D$ 重合)，设 $△ O D P$ 的外心为 $I$ ，则 $E I$ 的最小值为（）

A、 $1$ B、 $2$ C、 $2 \sqrt{3} - 1$ D、 $\sqrt{3} + 1$

查看试题解析

二、填空题

17. 8的立方根是．

查看试题解析
18. 下图是嘉琪同学计算 $\frac{m + 1}{m - 1} - \frac{4 m}{m^{2} - 1}$ 的过程.其中错误的是第步，正确的化简结果是．

查看试题解析
19. 如图， $△ O A_{1} B_{1} ， △ B_{1} A_{2} B_{2} ， △ B_{2} A_{3} B_{3}$ ...，都是等腰直角三角形，点 $B_{1} ， B_{2} ， B_{3} ，$ ...均在 $x$ 轴正半轴上，直角顶点 $A_{1} (2 ， 2) ， A_{2} ， A_{3}$ ...，均在直线 $l ： y = - \frac{1}{2} x + 3$ 上.设 $△ O A_{1} B_{1} ， △ B_{1} A_{2} B_{2} ， △ B_{2} A_{3} B_{3}$ 的面积分别为 $S_{1} ， S_{2} ， S_{3} ，$ ···，则 $S_{1} =$ ；依据图形所反映的规律， $S_{2020} =$ ．

查看试题解析

三、解答题

20. 数学老师给出这样一个题： □ $- 2 \times$ △ $= - x^{2} + 2 x$ .

(1)、若“ □ ”与“ △ ”相等，求“ △ ”(用含 $x$ 的代数式表示)；

(2)、若“□”为 $3 x^{2} - 2 x + 6$ ，当 $x = 1$ 时，请你求出“ △ ”的值.

查看试题解析
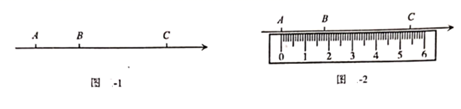21. 如图1，点 $A ， B ， C$ 是数轴上：从左到右排列的三个点，分别对应的数为 $- 5 ， b ， 4.$ 某同学将刻度尺如图2放置.使刻度尺上的数字 $0$ 对齐数轴上的点 $A$ ，发现点 $B$ 对齐刻度 $1.8 c m$ ，点 $C$ 对齐刻度 $5.4 c m$ .

(1)、在图1的数轴上， $A C =$ 个单位长度；数轴上的一个单位长度对应刻度尺上的 $c m$ .

(2)、求数轴上点 $B$ 所对应的数 $b$ ；

(3)、在图1的数轴上，点 $Q$ 是线段 $A B$ 上一点，满足 $A Q = 2 Q B ，$ 求点 $Q$ 所表示的数.

查看试题解析

22. 我市各学校积极响应上级“停课不停教、修课不停学”的要求，开展了空中在线教学.其校就“网络直播课”的满意度进行了随机在线问卷调在，调在结果分为四类： A．非常满意；B．很满意；C．一般；D．不满意，将收集到的信息进行了统计，绘制成如下不完整的统计表和统计图(如图所示).请你根据统计图表所提供的信息解答下列问题：

(1)、接受问卷调查的学生共有人；

m =

；

n =

；

(2)、补全条形统计图；

频数分布统计表

类别	频数	频率
$A$	$60$	$n$
$B$	$m$	$0.4$
$C$	$90$	$0.3$
$D$	$30$	$0.1$

(3)、若该校共有学生

3000

人，请你根据上述调查结果，估计该校对“网络直播课”满意度为

A

类和

B

类的学生共有多少人；

(4)、为改进教学，学校决定从选填结果是

D

类的学生中，选取甲、乙、丙、丁四人，随机抽取两名同学参与网络座谈会，求甲、乙两名同学同时被抽中的概率．

查看试题解析

23. 如图1.在 $▱ A B C D$ 中， $A B < B C ，$ 把 $▱ A B C D$ 沿对角线 $A C$ 所在的直线折叠，使点 $B$ 落在点 $E$ 处， $C E$ 交 $A D$ 于点 $F$ .连接 $D E$ .

(1)、求证： $△ A D E ≌ △ C E D$ ；

(2)、求证： $△ D E F$ 为等腰三角形；

(3)、将图1中 $△ A E C$ 的沿射线 $C A$ 方向平移得到 $△ A^{'} E^{'} C'$ (如图2所示) .若在 $▱ A B C D$ 中， $A B = A C = 2 ， B C = 2 \sqrt{3}$ . 当 $B A' = B C$ 时，直接写出 $△ A E C$ 平移的距离.

查看试题解析
24. 有甲、乙两家草莓采摘园，草莓的销售价格相间，在生长旺季，两家均排出优惠方案.甲园的优惠方案是：采摘的草莓不超过 $4 k g$ 时，按原价销售；若超过 $4 k g ，$ 超过部分 $6$ 折优惠；乙园的优惠方案是：游客进园需购买 $20$ 元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓 $14 k g$ 时，所需费用相同.
在乙采摘园所需费用 $y_{乙}$ ( 元)与草梅采摘量 $x$ (千克)满足一次函数关系，如下表：

数量 $x$ /千克

$0.5$

$1$

$1.5$

$2$

···

费用 $y_{乙} /$ 元

$y_{1}$

$y_{2}$

$50$

$60$

···

(1)、求 $y_{乙}$ 与 $x$ 的函数关系式(不必写出 $x$ 的范围)；

(2)、求两个采摘园的草莓在生长旺季前的销售价格.并求在甲采摘园所需费用 $y_{甲}$ (元)与草莓采摘量 $x$ (千克)的函数关系式 $(x > 4)$ ；

(3)、若嘉琪准备花费 $200$ 元去采摘草莓，去哪个园采摘，可以得到更多数量的草莓？说明理由.

查看试题解析
25. 如图1，在矩形 $A B C D$ 中， $A B = 9 ， B C = 12$ ，点 $P$ 是线段 $A D$ 上的一个动点，以点 $P$ 为圆心， $P D$ 为半径作 $⊙ P$ ，连接 $C P$ .

(1)、当 $⊙ P$ 经过 $P C$ 的中点时， $P C$ 的长为；

(2)、当 $C P$ 平分 $∠ A C D$ 时，判断 $A C$ 与 $⊙ P$ 的位置关系.说明理由，并求出 $P D$ 的长；

(3)、如图2，当 $⊙ P$ 与 $A C$ 交于 $E ， F$ 两点，且 $E F = 9.6$ 时，求点 $P$ 到 $A C$ 的距离．

查看试题解析
26. 如图，抛物线 $L ： y = a (x - 1) (x - 5)$ 与 $x$ 铀交于 $A ， B$ 两点(点 $A$ 作点 $B$ 的左侧)，与 $y$ 轴交于点 $C .$ 且 $O B = O C$ ，点 $P (m ， n)$ 为抛物线 $L$ 的对称轴右侧图象上的一点.

(1)、a的值为，抛物线的顶点坐标为；

(2)、设抛物线 $L$ 在点 $C$ 和点 $P$ 之间部分(含点 $C$ 和点 $P$ )的最高点与最低点的纵坐标之差为 $h$ ，求 $h$ 关于 $m$ 的函数表达式，并写出自变量 $m$ 的取值范围；

(3)、当点 $P (m ， n)$ 的坐标满足： $m + n = 19$ 时，连接 $P C ， P B ， A C$ ，若 $M$ 为线段 $P C$ 上一点，且 $B M$ 分四边形 $A B P C$ 的面积为相等两部分，求点 $M$ 的坐标.

查看试题解析

数量 $x$ /千克	$0.5$	$1$	$1.5$	$2$	···
费用 $y_{乙} /$ 元	$y_{1}$	$y_{2}$	$50$	$60$	···

成绩/分	$5$	$6$	$7$	$8$	$9$	$10$
人数/人	$x$	$y$	$6$	$8$	$5$	$4$