河北省蠡县2020年中考数学模拟试卷
试卷更新日期:2020-07-14 类型:中考模拟
一、单选题
-
1. 数学文化《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是:今有两数,若其意义相反,则分别叫做正数与负数.若向东走9米记作 米,则 米表示( )A、向东走5米 B、向西走5米 C、向东走4米 D、向两走4米2. 下列设计的图案中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、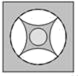 C、
C、 D、
D、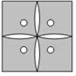 3. 在这次抗击新冠疫情的斗争中,全国共有13000多名90后医护驰援湖北.习近平主席在给北京大学援鄂医疗队全体“90后”党员的信中写到:“广大青年用行动证明,新时代的中国青年是好样的,是堪当大任的!”将13000用科学记数法表示应为( )A、 B、 C、 D、4.
3. 在这次抗击新冠疫情的斗争中,全国共有13000多名90后医护驰援湖北.习近平主席在给北京大学援鄂医疗队全体“90后”党员的信中写到:“广大青年用行动证明,新时代的中国青年是好样的,是堪当大任的!”将13000用科学记数法表示应为( )A、 B、 C、 D、4.如图所示某几何体的三视图,则这个几何体是( )
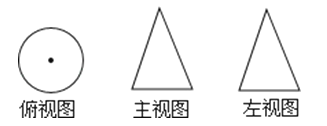 A、三棱锥 B、圆柱 C、球 D、圆锥5. 已知数轴上 , 两点间的距离为 ,若 表示数 ,则 表示的数为( )A、1 B、 C、0 D、26. 如图, ,则下列说法正确的是( )
A、三棱锥 B、圆柱 C、球 D、圆锥5. 已知数轴上 , 两点间的距离为 ,若 表示数 ,则 表示的数为( )A、1 B、 C、0 D、26. 如图, ,则下列说法正确的是( )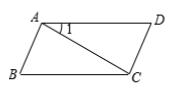 A、 B、 C、 D、7. 已知 ,则 的值为( )A、 B、0 C、1 D、不能确定8. 某生物小组观察一植物生长,得到的植物高度 (单位:厘米)与观察时间 (单位:天)的关系,并画出如下图所示的图象( 是线段,直线 平行于 轴).下列说法错误的是( )
A、 B、 C、 D、7. 已知 ,则 的值为( )A、 B、0 C、1 D、不能确定8. 某生物小组观察一植物生长,得到的植物高度 (单位:厘米)与观察时间 (单位:天)的关系,并画出如下图所示的图象( 是线段,直线 平行于 轴).下列说法错误的是( )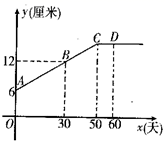 A、从开始观察时起,50天后该植物停止长高; B、直线 的函数表达式为 ; C、第40天,该植物的高度为14厘米; D、该植物最高为15厘米.9. 如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,则∠BCD的度数是( )
A、从开始观察时起,50天后该植物停止长高; B、直线 的函数表达式为 ; C、第40天,该植物的高度为14厘米; D、该植物最高为15厘米.9. 如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,则∠BCD的度数是( )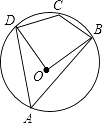 A、88° B、92° C、106° D、136°10. 一副三角板按如图方式摆放,且∠1的度数比∠2的度数大50°,若设∠1=x°,∠2=y°,则可得到方程组为( )
A、88° B、92° C、106° D、136°10. 一副三角板按如图方式摆放,且∠1的度数比∠2的度数大50°,若设∠1=x°,∠2=y°,则可得到方程组为( )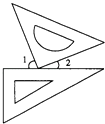 A、 B、 C、 D、11. 如图,在直角坐标系中,菱形 的顶点 在原点,点 的坐标为 ,点 的纵坐标是 ,则菱形 的边长为( )
A、 B、 C、 D、11. 如图,在直角坐标系中,菱形 的顶点 在原点,点 的坐标为 ,点 的纵坐标是 ,则菱形 的边长为( )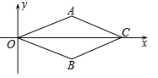 A、3 B、 C、5 D、12. 若实数a、b满足关系式: ( ),则直线 的图象经过的象限是( )A、第二、三、四象限 B、第一、三、四象限 C、第一、二、四象限 D、第一、二、三象限13. 如图,已知:图1,在 中, .小明的作法如图2所示,则他作出的两条线的交点 是 的( )
A、3 B、 C、5 D、12. 若实数a、b满足关系式: ( ),则直线 的图象经过的象限是( )A、第二、三、四象限 B、第一、三、四象限 C、第一、二、四象限 D、第一、二、三象限13. 如图,已知:图1,在 中, .小明的作法如图2所示,则他作出的两条线的交点 是 的( )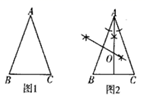 A、中心 B、内心 C、外心 D、垂心14. 某公司生产的一种产品按照质量由高到低分为A,B,C,D四级,为了增加产量、提高质量,该公司改进了一次生产工艺,使得生产总量增加了一倍.为了解新生产工艺的效果,对改进生产工艺前、后的四级产品的占比情况进行了统计,绘制了如下扇形图:
A、中心 B、内心 C、外心 D、垂心14. 某公司生产的一种产品按照质量由高到低分为A,B,C,D四级,为了增加产量、提高质量,该公司改进了一次生产工艺,使得生产总量增加了一倍.为了解新生产工艺的效果,对改进生产工艺前、后的四级产品的占比情况进行了统计,绘制了如下扇形图: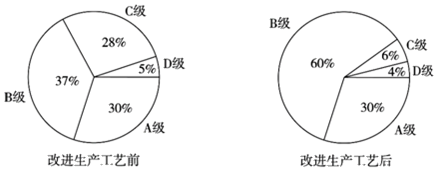
根据以上信息,下列推断合理的是( )
A、改进生产工艺后,A级产品的数量没有变化 B、改进生产工艺后,B级产品的数量增加了不到一倍 C、改进生产工艺后,C级产品的数量减少 D、改进生产工艺后,D级产品的数量减少15. 小明使用电脑软件探究函数 的图象,他输入了一组a,b的值,得到了下面的函数图象,由学习函数的经验,可以推断出小明输入的a,b的值满足( ) A、 , B、 , C、 , D、 ,
A、 , B、 , C、 , D、 ,二、填空题
-
16. 若正多边形的一个外角是40°,则这个正多边形的边数是.17. 分解因式: =。18. 如图,将 沿 方向平移 得到 ,如果 的周长为 ,那么四边形 的周长为 .
 19. 如图,在平面直角坐标系 中, , , , ,…,以 为对角线作第一个正方形 ,以 为对角线作第二个正方形 ,以 为对角线作第三个正方形 ,…,如果所作正方形的对角线 都在 轴上,且 的长度依次增加1个单位长度,顶点 都在第一象限内( ,且 为整数)那么 的纵坐标为;用 的代数式表示 的纵坐标.
19. 如图,在平面直角坐标系 中, , , , ,…,以 为对角线作第一个正方形 ,以 为对角线作第二个正方形 ,以 为对角线作第三个正方形 ,…,如果所作正方形的对角线 都在 轴上,且 的长度依次增加1个单位长度,顶点 都在第一象限内( ,且 为整数)那么 的纵坐标为;用 的代数式表示 的纵坐标.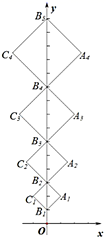
三、解答题
-
20. 老师在课余时间给同学们留下了如图所示的一个等式,让同学自己出题,并写出答案.
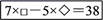 (1)、芳芳提出问题:当◇代表-2时,求□所代表的有理数;(2)、小宇提出的问题:若□和◇所代表的有理数互为相反数,求◇所代表的有理数.21. 在求两位数的平方时,可以用完全平方式及“列竖式”的方法进行速算,求解过程如下.
(1)、芳芳提出问题:当◇代表-2时,求□所代表的有理数;(2)、小宇提出的问题:若□和◇所代表的有理数互为相反数,求◇所代表的有理数.21. 在求两位数的平方时,可以用完全平方式及“列竖式”的方法进行速算,求解过程如下.例如:求 .
解:因为 ,将上式中等号右边的系数填入下面的表格中可得:
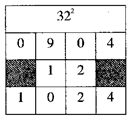
所以 .
(1)、下面是丽丽仿照例题求 的一部分过程,请你帮他写出最后结果;解:因为 ,将上式中等号右边的系数填入下面的表格中可得:
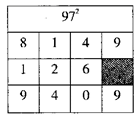
所以 ;
(2)、仿照例题,速算 ;
(备用表格)
(3)、琪琪用“列竖式”的方法计算一个两位数的平方,部分过程如下图所示.若这个两位数的个位数字为 ,则这个两位数为(用含 的代数式表示). 22. 某学校组织了一次体育测试,测试项目有A“立定跳远”、B“掷实心球”、C“仰卧起坐”、D“100米跑”、E“800米跑”.规定:每名学生测试三项,其中A、B为必测项目,第三项在C、D、E中随机抽取,每项10分(成绩均为整数且不低于0分).
22. 某学校组织了一次体育测试,测试项目有A“立定跳远”、B“掷实心球”、C“仰卧起坐”、D“100米跑”、E“800米跑”.规定:每名学生测试三项,其中A、B为必测项目,第三项在C、D、E中随机抽取,每项10分(成绩均为整数且不低于0分).甲
乙
(1)、完成A、B必测项目后,用列表法,求甲、乙两同学第三项抽取不同项目的概率;(2)、某班有6名男生抽到了E“800米跑”项目,他们的成绩分别(单位:分)为:x , 6,7,8,8,9.已知这组成绩的平均数和中位数相等,且x不是这组成绩中最高的,则x=;
(3)、该班学生丙因病错过了测试,补测抽到了E“800米跑”项目,加上丙同学的成绩后,发现这组成绩的众数与中位数相等,但平均数比原来的平均数小,则丙同学“800米跑”的成绩为多少?23. 如图, 是 的外接圆,连接 ,过点 作 交 的延长线于点 , . (1)、求证: 是 的切线;(2)、若 , 的半径为 ,求 的长.24. 如图,在平面直角坐标系 中,曲线 经过点 ,直线 与曲线 围成的封闭区域为图象 .
(1)、求证: 是 的切线;(2)、若 , 的半径为 ,求 的长.24. 如图,在平面直角坐标系 中,曲线 经过点 ,直线 与曲线 围成的封闭区域为图象 .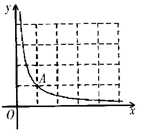 (1)、求曲线 的表达式;(2)、求出直线与曲线的交点坐标;(3)、直接写出图象 上的整数点个数有个,它们是.
(1)、求曲线 的表达式;(2)、求出直线与曲线的交点坐标;(3)、直接写出图象 上的整数点个数有个,它们是.(注:横,纵坐标均为整数的点称为整点,图象 包含边界)
25. 综合与实践问题情境
如图1, 和 均为等边三角形,点 , , 在同一条直线上,连接 ;
 (1)、探究发现
(1)、探究发现善思组发现: ,请你帮他们写出推理过程;
(2)、钻研组受善思组的启发,求出了 度数,请直接写出 等于度;(3)、奋进组在前面两组的基础上又探索出了 与 的位置关系为(请直接写出结果);(4)、拓展探究如图2, 和 均为等腰直角三角形, ,点 , , 在同一条直线上, 为 中 边上的高,连接 ,试探究 , , 之间有怎样的数量关系.

创新组类比善思组的发现,很快证出 ,进而得出 .请你写出 , , 之间的数量关系并帮创新组完成后续的证明过程.
26. 在平面直角坐标系xOy中,抛物线y=x2﹣2mx+m2﹣1与y轴交于点C.(1)、试用含m的代数式表示抛物线的顶点坐标;(2)、将抛物线y=x2﹣2mx+m2﹣1沿直线y=﹣1翻折,得到的新抛物线与y轴交于点D.若m>0,CD=8,求m的值;(3)、已知A(2k,0),B(0,k),在(2)的条件下,当线段AB与抛物线y=x2﹣2mx+m2﹣1只有一个公共点时,直接写出k的取值范围.