河北省保定市雄县2020年中考数学一模试卷
试卷更新日期:2020-07-14 类型:中考模拟
一、单选题
-
1. 计算: 的结果等于( )A、 B、 C、27 D、62. 下列运算正确的是( )A、 B、 C、 D、3. 下列各式正确的是( )A、 B、 C、 D、4. 将不等式组 的解集表示在数轴上,正确的是( )A、
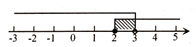 B、
B、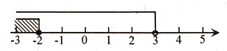 C、
C、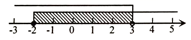 D、
D、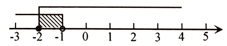 5. 若y轴上的点P到x轴的距离为3,则点P的坐标是( )A、(3,0) B、(0,3) C、(3,0)或(﹣3,0) D、(0,3)或(0,﹣3)6. 华为 手机搭载了全球首款7纳米制程芯片,7纳米就是0.000000007米.数据0.000000007用科学记数法表示为( ).A、 B、 C、 D、7. 计算 的结果为( )A、 B、 C、 D、8. 计算 ,正确的结果是( )A、1 B、 C、 a D、9. 小明同学对数据26,36,46,5■,52进行统计分析,发现其中一个两位数的个位数字被墨水涂污看不到了,则分析结果与被涂污数字无关的是 ( )A、平均数 B、方 C、中位数 D、众数10. 解分式方程 时,去分母变形正确的是( )A、 B、 C、 D、11. 如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是( )
5. 若y轴上的点P到x轴的距离为3,则点P的坐标是( )A、(3,0) B、(0,3) C、(3,0)或(﹣3,0) D、(0,3)或(0,﹣3)6. 华为 手机搭载了全球首款7纳米制程芯片,7纳米就是0.000000007米.数据0.000000007用科学记数法表示为( ).A、 B、 C、 D、7. 计算 的结果为( )A、 B、 C、 D、8. 计算 ,正确的结果是( )A、1 B、 C、 a D、9. 小明同学对数据26,36,46,5■,52进行统计分析,发现其中一个两位数的个位数字被墨水涂污看不到了,则分析结果与被涂污数字无关的是 ( )A、平均数 B、方 C、中位数 D、众数10. 解分式方程 时,去分母变形正确的是( )A、 B、 C、 D、11. 如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是( )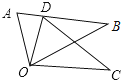 A、34° B、36° C、38° D、40°12. 下列四个函数图象中,当x>0时,y随x的增大而减小的是( )A、
A、34° B、36° C、38° D、40°12. 下列四个函数图象中,当x>0时,y随x的增大而减小的是( )A、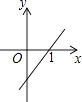 B、
B、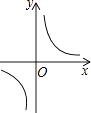 C、
C、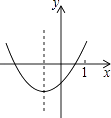 D、
D、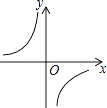 13. 当 时,关于 的一元二次方程 的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定14. 如图,在矩形 中, , ,过对角线交点 作 交 于点 ,交 于点 ,则 的长是( )
13. 当 时,关于 的一元二次方程 的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定14. 如图,在矩形 中, , ,过对角线交点 作 交 于点 ,交 于点 ,则 的长是( ) A、1 B、 C、2 D、15. 如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:
A、1 B、 C、2 D、15. 如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:①线段MN的长;
②△PAB的周长;
③△PMN的面积;
④直线MN,AB之间的距离;
⑤∠APB的大小.
其中会随点P的移动而变化的是( )
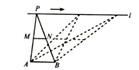 A、②③ B、②⑤ C、①③④ D、④⑤16. 定义:等腰三角形的顶角与其一个底角的度数的比值 称为这个等腰三角形的“特征值”.若等腰 中, ,则它的特征值k为( )A、 或 B、 或 C、 或4 D、 或4
A、②③ B、②⑤ C、①③④ D、④⑤16. 定义:等腰三角形的顶角与其一个底角的度数的比值 称为这个等腰三角形的“特征值”.若等腰 中, ,则它的特征值k为( )A、 或 B、 或 C、 或4 D、 或4二、填空题
-
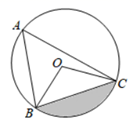
17. 当 时,代数式 的值等于 .18. 分解因式:19. 如图, 内接于 ,若 , 的半径 ,则阴影部分的面积为 .
 20. 如图,在 中, ,将 折叠,使点 , 分别落在点 , 处(点 , 都在 所在的直线上),折痕为 ,则 等于 .
20. 如图,在 中, ,将 折叠,使点 , 分别落在点 , 处(点 , 都在 所在的直线上),折痕为 ,则 等于 .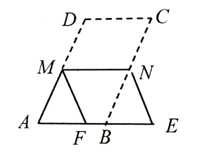
三、解答题
-
21.(1)、计算:(2)、解方程组:22. 方方驾驶小汽车匀速地从A地行使到B地,行驶里程为480千米,设小汽车的行使时间为t(单位:小时),行使速度为v(单位:千米/小时),且全程速度限定为不超过120千米/小时.(1)、求v关于t的函数表达式;(2)、方方上午8点驾驶小汽车从A出发.
①方方需在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v的范围.
②方方能否在当天11点30分前到达B地?说明理由.
23. 某企业为了解员工安全生产知识掌握情况,随机抽取了部分员工进行安全生产知识测试,测试试卷满分100分.测试成绩按 、 、 、 四个等级进行统计,并将统计结果绘制了如下两幅不完整的统计图.(说明:测试成绩取整数, 级:90分~100分; 级:75分-89分; 级:60分~74分; 级:60分以下)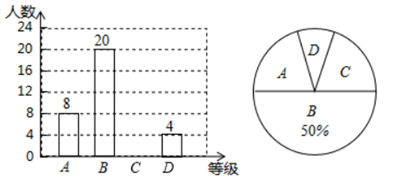
请解答下列问题:
(1)、该企业员工中参加本次安全生产知识测试共有人数;(2)、补全条形统计图;(3)、若该企业共有员工800人,试估计该企业员工中对安全生产知识的掌握能达到 级的人数.24. 如图,线段 ,射线 , 为射线 上一点,以 为边作正方形 ,且点 、 与点 在 两侧,在线段 上取一点 ,使 ,直线 与线段 相交于点 (点 与点 、 不重合).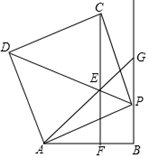 (1)、求证: ;(2)、判断 与 的位置关系,并说明理由;(3)、求 的周长.25. 已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.
(1)、求证: ;(2)、判断 与 的位置关系,并说明理由;(3)、求 的周长.25. 已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.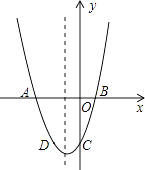 (1)、求抛物线的解析式;(2)、抛物线的对称轴上有一动点P,求出PA+PD的最小值;(3)、若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标.26. 如图,菱形 中,对角线 、 相交于点 , , ,动点 从点 出发,沿线段 以 的速度向点 运动,同时动点 从点 出发,沿线段 以 支向点 运动,当其中一个动点停止时另一个动点也随之停止,设运动时间为 (单位: )( ),以点 为圆心, 长为半径的⊙M与射线 、线段 分别交于点 、 ,连接 .
(1)、求抛物线的解析式;(2)、抛物线的对称轴上有一动点P,求出PA+PD的最小值;(3)、若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标.26. 如图,菱形 中,对角线 、 相交于点 , , ,动点 从点 出发,沿线段 以 的速度向点 运动,同时动点 从点 出发,沿线段 以 支向点 运动,当其中一个动点停止时另一个动点也随之停止,设运动时间为 (单位: )( ),以点 为圆心, 长为半径的⊙M与射线 、线段 分别交于点 、 ,连接 . (1)、求 的长(用含有 的代数式表示),并求出 的取值范围;(2)、当 为何值时,线段 与⊙M相切?(3)、若⊙M与线段 只有一个公共点,求 的取值范围.
(1)、求 的长(用含有 的代数式表示),并求出 的取值范围;(2)、当 为何值时,线段 与⊙M相切?(3)、若⊙M与线段 只有一个公共点,求 的取值范围.