2020年暑期衔接训练青岛版数学八年级下册：第6讲有理数、实数

试卷更新日期：2020-07-13 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列说法：（1）带根号的数是无理数；（2）无理数是带根号的数；（3）开方开不尽的都是无理数；（4）无理数都是开方开不尽的；（5）无理数是无限小数；（6）无限小数是无理数；正确的有（）.

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 下列实数 $\sqrt{π^{2}}$ ， $\sqrt{0.09}$ ，0， $\frac{22}{7}$ ，0.123456，0.1010010001，﹣ $\sqrt[3]{\frac{27}{8}}$ ， $\sqrt{0.4}$ ，﹣ $\sqrt[3]{100}$ ，无理数的个数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
3. 如图，矩形 $A B C D$ 中， $A B = 3$ ， $A D = 1$ ，点 $A$ ， $B$ 在数轴上，若以点 $A$ 为圆心，对角线 $A C$ 的长为半径作弧交数轴的正半轴于点 $M$ ，则点 $M$ 表示的数为（）．

A、 $\sqrt{10} - 1$ B、 $\sqrt{10}$ C、 $\sqrt{5} - 1$ D、 $\sqrt{5}$

查看试题解析
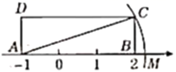4. 比较下列3个数： $2 \sqrt{7}$ ， $3 \sqrt{3}$ ， $\frac{1}{2} \sqrt{122}$ ，其中正确的顺序是（）

A、 $2 \sqrt{7} < 3 \sqrt{3} < \frac{1}{2} \sqrt{122}$ B、 $2 \sqrt{7} < \frac{1}{2} \sqrt{122} < 3 \sqrt{3}$ C、 $3 \sqrt{3} < 2 \sqrt{7} < \frac{1}{2} \sqrt{122}$ D、 $3 \sqrt{3} < \frac{1}{2} \sqrt{122} < 2 \sqrt{7}$

查看试题解析
5. 如图，数轴上的点A，B，O，C，D分别表示数-2，-1，0，1，2，则表示数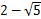的点P应落在

A、线段AB上 B、线段BO上 C、线段OC上 D、线段CD上

查看试题解析
6. 下列说法：（1）开方开不尽的数是无理数；（2）无理数包括正无理数、零、负无理数；（3）无限不循环小数是无理数；（4）无理数都可以用数轴上的点来表示
其中错误的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 下列说法，正确的有（）个
①m是一个实数，m²的算术平方根是m；②m是一个实数，则﹣m没有平方根；③带根号的数是无理数；④无理数是无限小数．

A、0 B、1 C、2 D、3

查看试题解析
8. 按如图所示的程序计算，若开始输入的n值为 $\sqrt{2}$ ，则最后输出的结果是（）

A、14 B、16 C、8+5 $\sqrt{2}$ D、14+ $\sqrt{2}$

查看试题解析
9. 实数a在数轴上的位置如图所示，则 $\sqrt{{(a - 2)}^{2}}$ + $\sqrt{{(a - 7)}^{2}}$ 化简后为（）

A、5 B、﹣5 C、2a﹣9 D、2a+5

查看试题解析
10. 如图，直径为1个单位长度的圆从A点沿数轴向右滚动（无滑动）两周到达点B，则点B表示的数是（）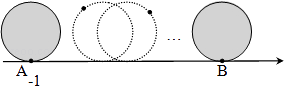

A、π B、2π C、2π﹣1 D、2π+1．

查看试题解析
11.
在数轴上标注了四段范围，如图所示，则表示﹣ $\sqrt{10}$ 的点落在（　　）

A、段① B、段② C、段③ D、段④

查看试题解析
12. 三个实数﹣ $\sqrt{6}$ ， ﹣2，﹣ $\sqrt{7}$ 之间的大小关系是（　　）

A、﹣ $\sqrt{7}$ ＞﹣ $\sqrt{6}$ ＞﹣2 B、﹣ $\sqrt{7}$ ＞﹣2＞﹣ $\sqrt{6}$ C、﹣2＞﹣ $\sqrt{6}$ ＞﹣ $\sqrt{7}$ D、﹣ $\sqrt{6}$ ＜﹣2＜﹣ $\sqrt{7}$

查看试题解析

二、填空题

13. 已知关于 $x$ 的一元一次不等式 $m x + 1 > 5 - 2 x$ 的解集是 $x < \frac{4}{m + 2}$ ，如图，数轴上的A，B，C，D四个点中，实数m对应的点可能是．

查看试题解析
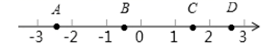14. 如图所示的数轴上，点B与点C关于点A对称，A、B两点对应的实数是 $\sqrt{3}$ 和﹣1，则点C所对应的实数是．

查看试题解析
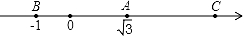15. 如图，点A，B在数轴上分别表示a，b，化简： $\sqrt{{(a + 1)}^{2}} - \sqrt{{(1 - b)}^{2}} + | a - b | + {(\sqrt{- a})}^{2}$ =.

查看试题解析
16. 对于任意不相等的两个数a，b，定义一种运算如下：a※b= $\frac{\sqrt{a + b}}{a - b}$ ，如3※2= $\frac{\sqrt{3 + 2}}{3 - 2}$ = $\sqrt{5}$ ，那么7※5= ．

查看试题解析
17. 下列说法：①如果两个三角形全等，那么这两个三角形一定成轴对称；②数轴上的点和实数一一对应；③ $\sqrt{3}$ 是3的一个平方根；④两个无理数的和一定为无理数；⑤6.9 $\times$ 10³精确到十分位；⑥ $\sqrt{16}$ 的平方根是 $\pm$ 4.其中正确的.（填序号）

查看试题解析
18. 如图，将有一边重合的两张直角三角形纸片放在数轴上，纸片上的点A表示的数是-2，AC=BC=BD=1。若以点A为圆心、AD的长为半径画弧，与数轴交于点E(点E位于点A右侧)，则点E表示的数为。

查看试题解析

三、作图题

19. 用直尺和圆规在如图所示的数轴上作出 $- \sqrt{2}$ 、 $\sqrt{13}$ 的点．保留作图痕迹

查看试题解析

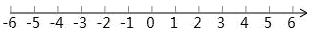
四、解答题

20. 计算： $| \sqrt{3} - 2 | + {(\frac{1}{2})}^{- 1} - {(3.14 - π)}^{0} - \sqrt{{(- 3)}^{2}}$ .

查看试题解析
21. 已知实数a、b、c、d、m，若a、b互为相反数，c、d互为倒数，m的绝对值是2，求 $\frac{a + b + m^{2} + 1}{\sqrt{c d}}$ 的平方根．

查看试题解析
22. 交通警察通常根据刹车后车轮滑过的距离估计车辆行驶的速度，所用的经验公式是v=16 $\sqrt{d f}$ ，其中v表示车速（单位：km/h），d表示刹车后车轮滑过的距离（单位：m），f表示摩擦因数．在某次交通事故中，测得d=6m，f=1.5，求肇事汽车的车速．

查看试题解析
23. 如图，数轴上有A．B两点，AB=12，原点O是线段AB上的一点，OA=2OB．

(1)、写出A，B两点所表示的实数；

(2)、若点C是线段AB上一点，且满足AC=CO+CB，求C点所表示的实数；

(3)、若动点P、Q分别从A．B同时出发，向右运动，点P的速度为每秒2个单位长度，点Q的速度为每秒1个单位长度，设运动时间为t秒，当点P与点Q重合时，P、Q两点停止运动．
①当t为何值时，2OP﹣OQ=4；
②当点P到达点O时，动点M从点O出发，以每秒3个单位长的速度也向右运动，当点M追上点Q后立即返回，以同样的速度向点P运动，遇到点P后再立即返回，以同样的速度向点Q运动，如此往返，直到点P、Q停止时，点M也停止运动，求在此过程中，点M行驶的总路程和点M最后位置在数轴上对应的实数．

查看试题解析
24. 我们知道：任意一个有理数与无理数的和为无理数，任意一个不为零的有理数与一个无理数的积为无理数，而零与无理数的积为零．由此可得：如果ax+b=0，其中a、b为有理数，x为无理数，那么a=0且b=0．
运用上述知识，解决下列问题：

(1)、如果（a+2） $\sqrt{2}$ -b+3=0，其中a、b为有理数，那么a= ， b=；

(2)、如果2b-a-（a+b-4） $\sqrt{3}$ =5，其中a、b为有理数，求3a+2b的平方根．

查看试题解析
25. 探究题：

(1)、若 $a$ 、 $b$ 、 $c$ 是有理数，且满足等式 $a + b \sqrt{2} + c \sqrt{3} = 2 - \sqrt{2} + 3 \sqrt{3}$ ，
试计算： ${(a - c)}^{2018} + b^{2017}$ 的值。

(2)、观察下列各式：
① $\sqrt{1 + \frac{1}{3}} = 2 \sqrt{\frac{1}{3}}$ ， $\sqrt{2 + \frac{1}{4}} = 3 \sqrt{\frac{1}{4}}$ ， $\sqrt{3 + \frac{1}{5}} = 4 \sqrt{\frac{1}{5}}$ ，
猜想： $\sqrt{5 + \frac{1}{7}}$ =；
②规律：用含 $n$ ( $n$ ≥1)的等式表示.

查看试题解析

2020年暑期衔接训练青岛版数学八年级下册：第6讲 有理数、实数

一、单选题

二、填空题

三、作图题

四、解答题

2020年暑期衔接训练青岛版数学八年级下册：第6讲有理数、实数