2020年暑期衔接训练青岛版数学八年级下册:第1讲 平行四边形的性质及判定
试卷更新日期:2020-07-13 类型:复习试卷
一、单选题
-
1. 在下列性质中,平行四边形不一定具有的是( )A、对边相等 B、对角互补 C、对边平行 D、对角相等2. 如图,在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=7,EF=3,则BC的长为( )
 A、11 B、12 C、13 D、143. 在四边形ABCD中,现有以下条件:①AB//CD,②A B=CD,③BC//AD,④BC=AD,从中任选两个使四边形ABCD为平行四边形的选法有( ).A、3种 B、4种 C、5种 D、6种4. 如图,平行四边形ABCD的周长为24cm , AC与BD相交于点O , OE⊥AC交AD于E , 则△DCE的周长为( )
A、11 B、12 C、13 D、143. 在四边形ABCD中,现有以下条件:①AB//CD,②A B=CD,③BC//AD,④BC=AD,从中任选两个使四边形ABCD为平行四边形的选法有( ).A、3种 B、4种 C、5种 D、6种4. 如图,平行四边形ABCD的周长为24cm , AC与BD相交于点O , OE⊥AC交AD于E , 则△DCE的周长为( )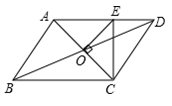 A、4cm B、16cm C、12cm D、24cm5. 如图,在平行四边形ABCD中,对角线AC和BD相交于O,∠BCA的平分线CE与边AB相交于E,若EB=EA=EC,那么下列结论正确的个数有( )
A、4cm B、16cm C、12cm D、24cm5. 如图,在平行四边形ABCD中,对角线AC和BD相交于O,∠BCA的平分线CE与边AB相交于E,若EB=EA=EC,那么下列结论正确的个数有( )①∠ACE=30°;②OE∥DA;③S▱ABCD=AC•AD;④CE⊥DB
 A、1 B、2 C、3 D、46. 如图,在▱ABCD中,AB=4,∠BAD的平分线与BC的延长线相交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的长为( )
A、1 B、2 C、3 D、46. 如图,在▱ABCD中,AB=4,∠BAD的平分线与BC的延长线相交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的长为( )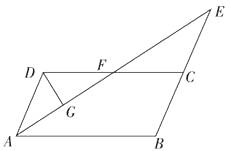 A、2 B、4 C、4 D、87. 如图,在平行四边形ABCD中,点A1 , A2 , A3 , A4和C1 , C2 , C3 , C4分别是AB和CD的五等分点,点B1 , B2和D1 , D2分别是BC和DA的三等分点.已知四边形A4B2C4D2的面积为18,则平行四边形ABCD的面积为( )
A、2 B、4 C、4 D、87. 如图,在平行四边形ABCD中,点A1 , A2 , A3 , A4和C1 , C2 , C3 , C4分别是AB和CD的五等分点,点B1 , B2和D1 , D2分别是BC和DA的三等分点.已知四边形A4B2C4D2的面积为18,则平行四边形ABCD的面积为( ) A、22 B、25 C、30 D、158.
A、22 B、25 C、30 D、158.小敬不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃.其编号应该是( )
 A、①,② B、①,④ C、③,④ D、②,③9. 如图,已知平行四边形ABCD的对角线的交点是0,直线EF过O点,且平行于AD,直线GH过0点且平行于AB,则图中平行四边形共有( )
A、①,② B、①,④ C、③,④ D、②,③9. 如图,已知平行四边形ABCD的对角线的交点是0,直线EF过O点,且平行于AD,直线GH过0点且平行于AB,则图中平行四边形共有( ) A、15个 B、16个 C、17个 D、18个10. 如图,在▱ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF,CF,则下列结论中不一定成立的是( )
A、15个 B、16个 C、17个 D、18个10. 如图,在▱ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF,CF,则下列结论中不一定成立的是( ) A、S△BEC=2S△CEF B、EF=CF C、∠DCF= ∠BCD D、∠DFE=3∠AEF
A、S△BEC=2S△CEF B、EF=CF C、∠DCF= ∠BCD D、∠DFE=3∠AEF二、填空题
-
11. 在平行四边形ABCD中,若 与 的度数之比为 ,则 的度数为 .12. 在平行四边形ABCD中,已知AB、BC、CD三条边的长度分别为(x+3),(x﹣4)和16,则这个四边形的周长是.13. 如图,在平行四边形ABCD中,AC=8,BD=6,AD=a,则a的取值范围是.
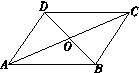 14. 如图,在平面直角坐标系中,四边形OABC是平行四边形,O(0,0),A(1,-2),B(3,1)则C点坐标为 .
14. 如图,在平面直角坐标系中,四边形OABC是平行四边形,O(0,0),A(1,-2),B(3,1)则C点坐标为 . 15. 如图,已知▱OABC的顶点A、C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为 .
15. 如图,已知▱OABC的顶点A、C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为 .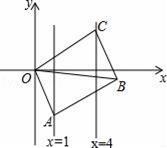 16. 在▱ABCD中,AB、BC、CD三条边的长度分别为(a﹣3)cm、(a﹣4)cm、(9﹣a)cm,则这个平行四边形的周长为 cm.17. 已知在直角坐标系中有A、B、C、D四个点,其中A,B,C三个点的坐标分别为(0,2),(﹣1,0),(2,0),则当点D的坐标为 时,以A、B、C、D四个点为顶点的四边形是平行四边形.18. 阅读下面材料:
16. 在▱ABCD中,AB、BC、CD三条边的长度分别为(a﹣3)cm、(a﹣4)cm、(9﹣a)cm,则这个平行四边形的周长为 cm.17. 已知在直角坐标系中有A、B、C、D四个点,其中A,B,C三个点的坐标分别为(0,2),(﹣1,0),(2,0),则当点D的坐标为 时,以A、B、C、D四个点为顶点的四边形是平行四边形.18. 阅读下面材料:在数学课上,老师提出如下问题:
已知:如图, 及 边的中点 .
求作:平行四边形 .

①连接 并延长,在延长线上截取 ;
②连接 、 .
所以四边形 就是所求作的平行四边形.

老师说:“小敏的作法正确.
请回答:小敏的作法正确的理由是 .
19. 如图,在四边形 中, ,点 分别从点 同时出发,点 以 的速度由点 向点 运动,点 以 的速度由点 向点 运动设运动时间为 .当 .时, 为平行四边形的一边. 20. 如图,平行四边形ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=2BG,连接AP,若S△PBG=2,则S四边形AEPH=.
20. 如图,平行四边形ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=2BG,连接AP,若S△PBG=2,则S四边形AEPH=.
三、作图题
-
21. 图①,图②均是 的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,点A在格点上.试在网格中画出顶点在格点上,面积为6,且符合相应条件的图形.
 (1)、在图①中,画出以点A为顶点的非特殊的平行四边形.(2)、在图②中,画出以点A为对角线交点的非特殊的平行四边形.
(1)、在图①中,画出以点A为顶点的非特殊的平行四边形.(2)、在图②中,画出以点A为对角线交点的非特殊的平行四边形.四、解答题
-
22. 如图,四边形ABCD是平行四边形,且DE∥BF,分别交对角线AC于点E、F,连接EB,FD.
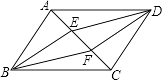
求证:BE∥DF.
23. 如图,把▱ABCD分成4个小平行四边形,已知▱AEOG,▱BFOG,▱CFOH的面积分别为8,10,30,求▱OEDH的面积.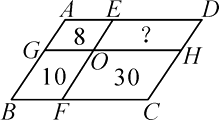 24. 如图,▱ABCD中, 的角平分线 交AD于点E, 的角平分线 交 于点 , ,DE=3, =50°.
24. 如图,▱ABCD中, 的角平分线 交AD于点E, 的角平分线 交 于点 , ,DE=3, =50°. (1)、求 的度数;(2)、求▱ABCD的周长.25. 如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,BE=DF.
(1)、求 的度数;(2)、求▱ABCD的周长.25. 如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,BE=DF. (1)、求证:∠1=∠2;(2)、求证:AF∥CE.26. 如图,在平面直角坐标系中,点A (0,4).动点P从原点O出发,沿x轴正方向以每秒2个单位的速度运动,同时动点Q从点A出发,沿y轴负方向以每秒1个单位的速度运动,以QO、QP为邻边构造平行四边形OQPB,在线段OP的延长线长取点C,使得PC=2,连接BC、CQ.设点P、Q运动的时间为t(0<t<4)秒.
(1)、求证:∠1=∠2;(2)、求证:AF∥CE.26. 如图,在平面直角坐标系中,点A (0,4).动点P从原点O出发,沿x轴正方向以每秒2个单位的速度运动,同时动点Q从点A出发,沿y轴负方向以每秒1个单位的速度运动,以QO、QP为邻边构造平行四边形OQPB,在线段OP的延长线长取点C,使得PC=2,连接BC、CQ.设点P、Q运动的时间为t(0<t<4)秒. (1)、用含t的代数式表示:
(1)、用含t的代数式表示:点B的坐标 , 点C的坐标;
(2)、当t=1时:①四边形QOBC的面积为;②在平面内存在一点D,使得以点Q、B、C、D为顶点的四边形是平行四边形,直接写出此时点D的坐标.
-