2020年暑期衔接训练青岛版数学八年级下册:第5讲 勾股定理
试卷更新日期:2020-07-13 类型:复习试卷
一、单选题
-
1. 已知直角三角形的两边长分别为3,5,则第三边长为( )A、4 B、4或 C、 D、4或2. 将一根 24cm 的筷子,置于底面直径为 15cm , 高 8cm 的装满水的无盖圆柱形水杯中,设筷子浸没在杯子里面的长度为 hcm , 则 h 的取值范围是( )A、h≤15cm B、h≥8cm C、8cm≤h≤17cm D、7cm≤h≤16cm3. 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为 ,则正方形A,B,C,D的面积之和为( )
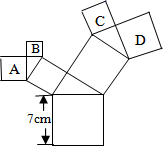 A、 B、 C、 D、4. 边长为5的菱形ABCD按如图所示放置在数轴上, 其中A点表示数-2,C点表示数6,则BD=( )
A、 B、 C、 D、4. 边长为5的菱形ABCD按如图所示放置在数轴上, 其中A点表示数-2,C点表示数6,则BD=( )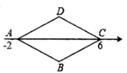 A、4 B、6 C、8 D、105. 如图,Rt△ABC中,∠ACB=90°,以AC,BC为直径作半圆S1和S2 , 且S1+S2=2π,则AB的长为( )
A、4 B、6 C、8 D、105. 如图,Rt△ABC中,∠ACB=90°,以AC,BC为直径作半圆S1和S2 , 且S1+S2=2π,则AB的长为( )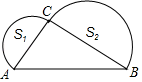 A、16 B、8 C、4 D、26. 下列说法正确的是( )A、若 a、b、c是△ABC的三边,则a2+b2=c2 B、若 a、b、c是Rt△ABC的三边,则a2+b2=c2 C、若 a、b、c是Rt△ABC的三边, ,则a2+b2=c2 D、若 a、b、c是Rt△ABC的三边, ,则a2+b2=c27. 如图,在平面直角坐标系中,点P的坐标为(-2,3),以点O为圆心,OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标为( )
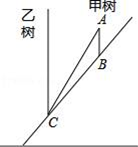
A、16 B、8 C、4 D、26. 下列说法正确的是( )A、若 a、b、c是△ABC的三边,则a2+b2=c2 B、若 a、b、c是Rt△ABC的三边,则a2+b2=c2 C、若 a、b、c是Rt△ABC的三边, ,则a2+b2=c2 D、若 a、b、c是Rt△ABC的三边, ,则a2+b2=c27. 如图,在平面直角坐标系中,点P的坐标为(-2,3),以点O为圆心,OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标为( ) A、 B、 C、 D、8. 如图,一棵大树在离地面3 ,5 两处折成三段,中间一段 恰好与地面平行,大树顶部落在离大树底部6 处,则大树折断前的高度是( )
A、 B、 C、 D、8. 如图,一棵大树在离地面3 ,5 两处折成三段,中间一段 恰好与地面平行,大树顶部落在离大树底部6 处,则大树折断前的高度是( ) A、 B、 C、 D、9. 如图,设小方格的面积为1,则图中以格点为端点且长度为 的线段有( )
A、 B、 C、 D、9. 如图,设小方格的面积为1,则图中以格点为端点且长度为 的线段有( )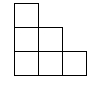 A、2条 B、3条 C、4条 D、5条10. 我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的大正方形,如图所示,如果大正方形的面积是13,小正方形的面积为1,直角三角形的较短直角边长为a , 较长直角边长为b , 那么(a+b)2的值为( )
A、2条 B、3条 C、4条 D、5条10. 我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的大正方形,如图所示,如果大正方形的面积是13,小正方形的面积为1,直角三角形的较短直角边长为a , 较长直角边长为b , 那么(a+b)2的值为( ) A、13 B、19 C、25 D、16911. 如图,长方体的底面是边长为6的正方形,高为8,点A离点C的距离是3,点B离点D的距离是2.一只蚂蚁沿长方体表面从点A爬到点B,其最短距离是()
A、13 B、19 C、25 D、16911. 如图,长方体的底面是边长为6的正方形,高为8,点A离点C的距离是3,点B离点D的距离是2.一只蚂蚁沿长方体表面从点A爬到点B,其最短距离是()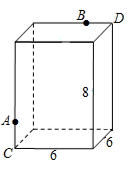 A、 B、 C、 D、1012. 如图,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为( )
A、 B、 C、 D、1012. 如图,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为( )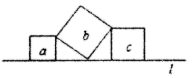 A、6 B、8 C、16 D、55
A、6 B、8 C、16 D、55二、填空题
-
13. 生活经验表明:靠墙摆放梯子时,若梯子底端离墙约为梯子长度的 时,则梯子比较稳定.现有一长度为9 m的梯子,当梯子稳定摆放时,它的顶端能到达8.5 m高的墙头吗?(填“能”或“不能”).14. 我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为 4 的正方形ABCD的边AB在轴x上,AB的中点是坐标原点O固定点A,B, 把正方形沿箭头方向推,使点 D落在y 轴正半轴上点 D′处,则点C的对应点C′的坐标为
 15. 如图,Rt△ABC中,∠C=90°,D、E分别是边AB、AC的点,将△ABC沿DE折叠,使点A的对称点A′恰好落在BC的中点处.若AB=10,BC=6,则AE的长为 .
15. 如图,Rt△ABC中,∠C=90°,D、E分别是边AB、AC的点,将△ABC沿DE折叠,使点A的对称点A′恰好落在BC的中点处.若AB=10,BC=6,则AE的长为 . 16. 如图,用两个边长分别为a、b、c的直角三角形(c为斜边)和一个腰长为c的等腰直角三角形拼成一个梯形,用两种不同方法计算这个图形的面积,得到的一个关于a、b、c的等式是 .
16. 如图,用两个边长分别为a、b、c的直角三角形(c为斜边)和一个腰长为c的等腰直角三角形拼成一个梯形,用两种不同方法计算这个图形的面积,得到的一个关于a、b、c的等式是 . 17. 如图,A、B是网格中的两个格点,点C也是网格中的一个格点,连接AB、BC、AC,当△ABC为等腰三角形时,设网格中的每个小正方形的边长为1,则所有满足题意的等腰三角形ABC的面积之和等于 .
17. 如图,A、B是网格中的两个格点,点C也是网格中的一个格点,连接AB、BC、AC,当△ABC为等腰三角形时,设网格中的每个小正方形的边长为1,则所有满足题意的等腰三角形ABC的面积之和等于 .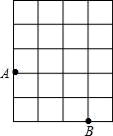 18. 如图,OP=1,过P作PP1⊥OP , 得OP1= ;再过P1作P1P2⊥OP1且P1P2=1,得OP2= ;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依此法继续作下去,得OP2019= .
18. 如图,OP=1,过P作PP1⊥OP , 得OP1= ;再过P1作P1P2⊥OP1且P1P2=1,得OP2= ;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依此法继续作下去,得OP2019= . 19. 如图,圆柱形玻璃杯高为13cm,底面周长为40cm,在杯内壁离底1cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁到内壁B处的最短距离为 .
19. 如图,圆柱形玻璃杯高为13cm,底面周长为40cm,在杯内壁离底1cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁到内壁B处的最短距离为 . 20. 如图,在矩形 中, , ,点 从点 出发,以每秒2个单位长度的速度沿 向点 运动,同时点 从点 出发,以每秒1个单位长度的速度沿 向点 运动,当点 到达点 时,点 , 同时停止运动.连接 , ,设点 运动的时间为 ,若 是以 为底的等腰三角形,则 的值为 .
20. 如图,在矩形 中, , ,点 从点 出发,以每秒2个单位长度的速度沿 向点 运动,同时点 从点 出发,以每秒1个单位长度的速度沿 向点 运动,当点 到达点 时,点 , 同时停止运动.连接 , ,设点 运动的时间为 ,若 是以 为底的等腰三角形,则 的值为 .
三、作图题
-
21. 如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
 (1)、在图(1)中以格点为顶点画一个面积为10的正方形;(2)、在图(2)中以格点为顶点画一个三角形,使三角形三边长分别为2, , .
(1)、在图(1)中以格点为顶点画一个面积为10的正方形;(2)、在图(2)中以格点为顶点画一个三角形,使三角形三边长分别为2, , .四、解答题
-
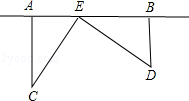
22. 为了丰富少年儿童的业余生活,某社区要在如图中的AB所在的直线上建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B.已知AB=2.5km,CA=1.5km,DB=1.Okm,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?
 23. 数学综合实验课上,同学们在测量学校旗杆的高度时发现:将旗杆顶端升旗用的绳子垂到地面还多2米;当把绳子的下端拉开8米后,下端刚好接触地面,如图,根据以上数据,同学们准确求出了旗杆的高度,你知道他们是如何计算出来的吗?
23. 数学综合实验课上,同学们在测量学校旗杆的高度时发现:将旗杆顶端升旗用的绳子垂到地面还多2米;当把绳子的下端拉开8米后,下端刚好接触地面,如图,根据以上数据,同学们准确求出了旗杆的高度,你知道他们是如何计算出来的吗?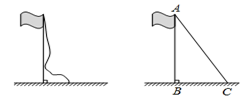 24. 如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF,通过用不同方法计算梯形ABEF的面积可验证一条我们学过的定理,该定理的名称是 , 请你写出证明的过程。
24. 如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF,通过用不同方法计算梯形ABEF的面积可验证一条我们学过的定理,该定理的名称是 , 请你写出证明的过程。 25. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,顶端距离地面的高度AC为2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面的高度A′D为2米,求小巷的宽度.
25. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,顶端距离地面的高度AC为2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面的高度A′D为2米,求小巷的宽度.
-