2020年山东省高考数学真题试卷（新高考Ⅰ卷)

试卷更新日期：2020-07-13 类型：高考真卷

进入出卷网下载

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 设集合A={x|1≤x≤3}，B={x|2<x<4}，则A∪B=（）

A、{x|2<x≤3} B、{x|2≤x≤3} C、{x|1≤x<4} D、{x|1<x<4}

查看试题解析
2. $\frac{2 - i}{1 + 2 i} =$ （）

A、1 B、−1 C、i D、−i

查看试题解析
3. 6名同学到甲、乙、丙三个场馆做志愿者，每名同学只去1个场馆，甲场馆安排1名，乙场馆安排2名，丙场馆安排3名，则不同的安排方法共有（）

A、120种 B、90种 C、60种 D、30种

查看试题解析
4. 日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球(球心记为O)，地球上一点A的纬度是指OA与地球赤道所在平面所成角，点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷，若晷面与赤道所在平面平行，点A处的纬度为北纬40°，则晷针与点A处的水平面所成角为（）

A、20° B、40° C、50° D、90°

查看试题解析
5. 某中学的学生积极参加体育锻炼，其中有96%的学生喜欢足球或游泳，60%的学生喜欢足球，82%的学生喜欢游泳，则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是（）

A、62% B、56% C、46% D、42%

查看试题解析
6. 基本再生数R₀与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数，世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段，可以用指数模型： $I (t) = e^{r t}$ 描述累计感染病例数I(t)随时间t(单位:天)的变化规律，指数增长率r与R₀ ， T近似满足R₀ =1+rT.有学者基于已有数据估计出R₀=3.28，T=6.据此，在新冠肺炎疫情初始阶段，累计感染病例数增加1倍需要的时间约为(ln2≈0.69) （）

A、1.2天 B、1.8天 C、2.5天 D、3.5天

查看试题解析
7. 已知P是边长为2的正六边形ABCDEF内的一点，则 $\vec{A P} \cdot \vec{A B}$ 的取值范围是（）

A、 $(- 2 ， 6)$ B、 $(- 6 ， 2)$ C、 $(- 2 ， 4)$ D、 $(- 4 ， 6)$

查看试题解析
8. 若定义在R的奇函数f(x)在 $(- \infty ， 0)$ 单调递减，且f(2)=0，则满足 $x f (x - 1) \geq 0$ 的x的取值范围是（）

A、 $[- 1 ， 1] \cup [3 ， + \infty)$ B、 $[- 3 ， - 1] \cup [0 ， 1]$ C、 $[- 1 ， 0] \cup [1 ， + \infty)$ D、 $[- 1 ， 0] \cup [1 ， 3]$

查看试题解析

二、选择题：本小题共4小题，每小题5分，共20分。在每小题给出的选项中，有多项符合题目要求。全部选对的得5分，有选错的得0分，部分选对的得3分。

9. 已知曲线 $C : m x^{2} + n y^{2} = 1$ .（）

A、若m>n>0，则C是椭圆，其焦点在y轴上 B、若m=n>0，则C是圆，其半径为 $\sqrt{n}$ C、若mn<0，则C是双曲线，其渐近线方程为 $y = \pm \sqrt{- \frac{m}{n}} x$ D、若m=0，n>0，则C是两条直线

查看试题解析
10. 下图是函数y= sin(ωx+φ)的部分图像，则sin(ωx+φ)= （）

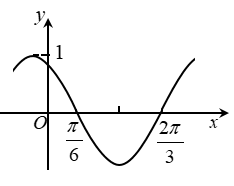
A、 $sin(x + \frac{π}{3} ）$ B、 $sin(\frac{π}{3} - 2 x)$ C、 $cos(2 x + \frac{π}{6} ）$ D、 $cos(\frac{5 π}{6} - 2 x)$

查看试题解析
11. 已知a>0，b>0，且a+b=1，则（）

A、 $a^{2} + b^{2} \geq \frac{1}{2}$ B、 $2^{a - b} > \frac{1}{2}$ C、 $\log_{2} a + \log_{2} b \geq - 2$ D、 $\sqrt{a} + \sqrt{b} \leq \sqrt{2}$

查看试题解析
12. 信息熵是信息论中的一个重要概念.设随机变量X所有可能的取值为 $1, 2, \dots, n$ ，且 $P (X = i) = p_{i} > 0 (i = 1, 2, \dots, n), \sum_{i = 1}^{n} p_{i} = 1$ ，定义X的信息熵 $H (X) = - \sum_{i = 1}^{n} p_{i} \log_{2} p_{i}$ .（）

A、若n=1，则H(X)=0 B、若n=2，则H(X)随着 $p_{1}$ 的增大而增大 C、若 $p_{i} = \frac{1}{n} (i = 1, 2, \dots, n)$ ，则H(X)随着n的增大而增大 D、若n=2m，随机变量Y所有可能的取值为 $1, 2, \dots, m$ ，且 $P (Y = j) = p_{j} + p_{2 m + 1 - j} (j = 1, 2, \dots, m)$ ，则H(X)≤H(Y)

查看试题解析

三、填空题(本大题共4小题，每小题5分，共20分)

13. 斜率为 $\sqrt{3}$ 的直线过抛物线C：y²=4x的焦点，且与C交于A，B两点，则 $| A B |$ = ．

查看试题解析
14. 将数列{2n–1}与{3n–2}的公共项从小到大排列得到数列{a_n}，则{a_n}的前n项和为．

查看试题解析
15. 某中学开展劳动实习，学生加工制作零件，零件的截面如图所示．O为圆孔及轮廓圆弧AB所在圆的圆心，A是圆弧AB与直线AG的切点，B是圆弧AB与直线BC的切点，四边形DEFG为矩形，BC⊥DG，垂足为C，tan∠ODC= $\frac{3}{5}$ ， $B H ∥ D G$ ，EF=12 cm，DE=2 cm，A到直线DE和EF的距离均为7 cm，圆孔半径为1 cm，则图中阴影部分的面积为cm² ．

查看试题解析
16. 已知直四棱柱ABCD–A₁B₁C₁D₁的棱长均为2，∠BAD=60°．以 $D_{1}$ 为球心， $\sqrt{5}$ 为半径的球面与侧面BCC₁B₁的交线长为．

查看试题解析

四、解答题(本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤)

17. 在① $a c = \sqrt{3}$ ，② $c sin A = 3$ ，③ $c = \sqrt{3} b$ 这三个条件中任选一个，补充在下面问题中，若问题中的三角形存在，求 $c$ 的值；若问题中的三角形不存在，说明理由．
问题：是否存在 $△ A B C$ ，它的内角 $A, B, C$ 的对边分别为 $a, b, c$ ，且 $sin A = \sqrt{3} sin B$ ， $C = \frac{π}{6}$ ， ▲ ?

注：如果选择多个条件分别解答，按第一个解答计分．

查看试题解析
18. 已知公比大于1的等比数列 ${a_{n}}$ 满足 $a_{2} + a_{4} = 20, a_{3} = 8$ ．

(1)、求 ${a_{n}}$ 的通项公式；

(2)、记 $b_{m}$ 为 ${a_{n}}$ 在区间 $(0, m] (m \in N^{*})$ 中的项的个数，求数列 ${b_{m}}$ 的前100项和 $S_{100}$ ．

查看试题解析

19. 为加强环境保护，治理空气污染，环境监测部门对某市空气质量进行调研，随机抽查了100天空气中的

PM 2.5

和

{SO}_{2}

浓度（单位：

μ {g/m}^{3}

），得下表：

${SO}_{2}$ $PM 2.5$	$[0, 50]$	$(50, 150]$	$(150, 475]$

$[0, 35]$	32	18	4
$(35, 75]$	6	8	12
$(75, 115]$	3	7	10

附： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，

$P (K^{2} \geq k)$	0.050 0.010 0.001
$k$	3.841 6.635 10.828

(1)、估计事件“该市一天空气中

PM 2.5

浓度不超过75，且

{SO}_{2}

浓度不超过150”的概率；

(2)、根据所给数据，完成下面的

2 \times 2

列联表：

${SO}_{2}$

$PM 2.5$

$[0, 150]$

$(150, 475]$

$[0, 75]$

$(75, 115]$

(3)、根据（2）中的列联表，判断是否有

99 %

的把握认为该市一天空气中

PM 2.5

浓度与

{SO}_{2}

浓度有关？

查看试题解析

20. 如图，四棱锥P-ABCD的底面为正方形，PD⊥底面ABCD．设平面PAD与平面PBC的交线为l．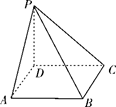

(1)、证明：l⊥平面PDC；

(2)、已知PD=AD=1，Q为l上的点，求PB与平面QCD所成角的正弦值的最大值．

查看试题解析
21. 已知函数 $f (x) = a e^{x - 1} - \ln x + \ln a$ ．

(1)、当 $a = e$ 时，求曲线y=f（x）在点（1，f（1））处的切线与两坐标轴围成的三角形的面积；

(2)、若f（x）≥1，求a的取值范围．

查看试题解析
22. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{\sqrt{2}}{2}$ ，且过点A（2，1）．

(1)、求C的方程：

(2)、点M，N在C上，且AM⊥AN，AD⊥MN，D为垂足．证明：存在定点Q，使得|DQ|为定值．

查看试题解析