2020年高考数学真题试卷(天津卷)
试卷更新日期:2020-07-13 类型:高考真卷
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 设全集 ,集合 ,则 ( )A、 B、 C、 D、2. 设 ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件3. 函数 的图象大致为( )A、
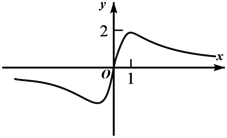 B、
B、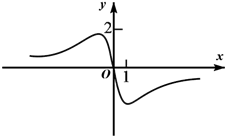 C、
C、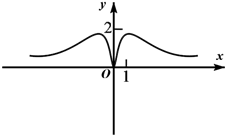 D、
D、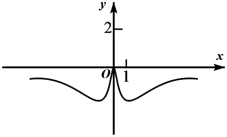 4. 从一批零件中抽取80个,测量其直径(单位: ),将所得数据分为9组: ,并整理得到如下频率分布直方图,则在被抽取的零件中,直径落在区间 内的个数为( )
4. 从一批零件中抽取80个,测量其直径(单位: ),将所得数据分为9组: ,并整理得到如下频率分布直方图,则在被抽取的零件中,直径落在区间 内的个数为( )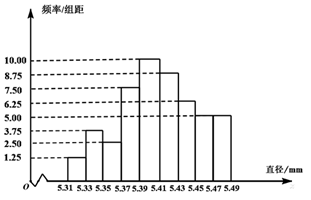
A、10 B、18 C、20 D、365. 若棱长为 的正方体的顶点都在同一球面上,则该球的表面积为( )A、 B、 C、 D、6. 设 ,则 的大小关系为( )A、 B、 C、 D、7. 设双曲线 的方程为 ,过抛物线 的焦点和点 的直线为l.若C的一条渐近线与 平行,另一条渐近线与l垂直,则双曲线C的方程为( )A、 B、 C、 D、8. 已知函数 .给出下列结论:① 的最小正周期为 ;② 是 的最大值;③把函数 的图象上所有点向左平移 个单位长度,可得到函数 的图象.其中所有正确结论的序号是( )
A、① B、①③ C、②③ D、①②③9. 已知函数 若函数 恰有4个零点,则k的取值范围是( )A、 B、 C、 D、二、填空题:本大题共6小题,每小题5分,共30分.试题中包含两个空的,答对1个的给3分,全部答对的给5分,
-
10. i是虚数单位,复数 .11. 在 的展开式中, 的系数是 .12. 已知直线 和圆 相交于 两点.若 ,则 的值为 .13. 已知甲、乙两球落入盒子的概率分别为 和 .假定两球是否落入盒子互不影响,则甲、乙两球都落入盒子的概率为;甲、乙两球至少有一个落入盒子的概率为 .14. 已知 ,且 ,则 的最小值为 .15. 如图,在四边形 中, , ,且 ,则实数 的值为 , 若 是线段 上的动点,且 ,则 的最小值为 .
三、解答题:本大题共5小题,共75分,解答应写出文字说明,证明过程或演算步骤.
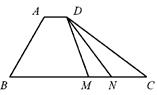
-
16. 在 中,角 所对的边分别为 .已知 .
(Ⅰ)求角C的大小;
(Ⅱ)求 的值;
(Ⅲ)求 的值.
17. 如图,在三棱柱 中, 平面 , ,点 分别在棱 和棱 上,且 为棱 的中点.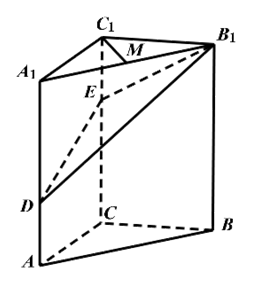
(Ⅰ)求证: ;(Ⅱ)求二面角 的正弦值;
(Ⅲ)求直线 与平面 所成角的正弦值.