2020年高考数学真题试卷（浙江卷）

试卷更新日期：2020-07-13 类型：高考真卷

进入出卷网下载

一、选择题：本大题共10小题，每小题4分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 已知集合P＝{x|1＜x＜4}，Q＝{x|2＜x＜3}，则P∩Q＝（）

A、{x|1＜x≤2} B、{x|2＜x＜3} C、{x|3≤x＜4} D、{x|1＜x＜4}

查看试题解析
2. 已知a∈R，若a﹣1+（a﹣2）i（i为虚数单位）是实数，则a＝（）

A、1 B、﹣1 C、2 D、﹣2

查看试题解析
3. 若实数x，y满足约束条件 ${\begin{matrix} x - 3 y + 1 \leq 0 \\ x + y - 3 \geq 0 \end{matrix}$ ，则z＝x+2y的取值范围是（）

A、（﹣∞，4] B、[4，+∞） C、[5，+∞） D、（﹣∞，+∞）

查看试题解析
4. 函数y＝xcosx+sinx在区间[﹣π，+π]的图象大致为（）

A、 B、 C、 D、

查看试题解析
5. 某几何体的三视图（单位：cm）如图所示，则该几何体的体积（单位：cm³）是（）

A、 $\frac{7}{3}$ B、 $\frac{14}{3}$ C、3 D、6

查看试题解析
6. 已知空间中不过同一点的三条直线m，n，l，则“m，n，l在同一平面”是“m，n，l两两相交”的（）

A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
7. 已知等差数列{a_n}的前n项和S_n ，公差d≠0， $\frac{a_{1}}{d}$ ≤1．记b₁＝S₂ ， b_n+1＝S_2n+2﹣S_2n ， n∈N*，下列等式不可能成立的是（）

A、2a₄＝a₂+a₆ B、2b₄＝b₂+b₆ C、a₄²＝a₂a₈ D、b₄²＝b₂b₈

查看试题解析
8. 已知点O（0，0），A（﹣2，0），B（2，0）．设点P满足|PA|﹣|PB|＝2，且P为函数y＝3 $\sqrt{4 - x^{2}}$ 图象上的点，则|OP|＝（）

A、 $\frac{\sqrt{22}}{2}$ B、 $\frac{4 \sqrt{10}}{5}$ C、 $\sqrt{7}$ D、 $\sqrt{10}$

查看试题解析
9. 已知a，b∈R且ab≠0，若（x﹣a）（x﹣b）（x﹣2a﹣b）≥0在x≥0上恒成立，则（）

A、a＜0 B、a＞0 C、b＜0 D、b＞0

查看试题解析
10. 设集合S，T，S⊆N*，T⊆N*，S，T中至少有两个元素，且S，T满足：
①对于任意x，y∈S，若x≠y，都有xy∈T；②对于任意x，y∈T，若x＜y，则 $\frac{y}{x}$ ∈S；下列命题正确的是（）

A、若S有4个元素，则S∪T有7个元素 B、若S有4个元素，则S∪T有6个元素 C、若S有3个元素，则S∪T有4个元素 D、若S有3个元素，则S∪T有5个元素

查看试题解析

二、填空题：本大题共7小题，共36分。多空题每小题6分；单空题每小题4分。

11. 已知数列{a_n}满足a_n＝ $\frac{n (n + 1)}{2}$ ，则S₃＝．

查看试题解析
12. 设（1+2x）⁵＝a₀+a₁x+a₂x²+a₃x³+a₄x⁴+a₅x⁵ ，则a₄＝；a₁+a₂+a₃＝．

查看试题解析
13. 已知tanθ＝2，则cos2θ＝；tan（θ﹣ $\frac{π}{4}$ ）＝．

查看试题解析
14. 已知圆锥展开图的侧面积为2π，且为半圆，则底面半径为．

查看试题解析
15. 设直线l：y＝kx+b（k＞0），圆C₁：x²+y²＝1，C₂：（x﹣4）²+y²＝1，若直线l与C₁ ， C₂都相切，则k＝；b＝．

查看试题解析
16. 一个盒子里有1个红1个绿2个黄四个相同的球，每次拿一个，不放回，拿出红球即停，设拿出黄球的个数为ξ，则P（ξ＝0）＝；E（ξ）＝．

查看试题解析
17. 设 $\vec{e_{1}}$ ， $\vec{e_{2}}$ 为单位向量，满足|2 $\vec{e_{1}}$ ﹣ $\vec{e_{2}}$ |≤ $\sqrt{2}$ ， $\vec{a}$ ＝ $\vec{e_{1}}$ + $\vec{e_{2}}$ ， $\vec{b}$ ＝3 $\vec{e_{1}}$ + $\vec{e_{2}}$ ，设 $\vec{a}$ ， $\vec{b}$ 的夹角为θ，则cos²θ的最小值为．

查看试题解析

三、解答题：本大题共5小题，共74分。解答应写出文字说明，证明过程或演算步骤。

18. 在锐角△ABC中，角A，B，C的对边分别为a，b，c，且2bsinA＝ $\sqrt{3}$ a．
（Ⅰ）求角B；

（Ⅱ）求cosA+cosB+cosC的取值范围．

查看试题解析
19. 如图，三棱台DEF﹣ABC中，面ADFC⊥面ABC，∠ACB＝∠ACD＝45°，DC＝2BC．
（Ⅰ）证明：EF⊥DB；

（Ⅱ）求DF与面DBC所成角的正弦值．

查看试题解析
20. 已知数列{a_n}，{b_n}，{c_n}中，a₁＝b₁＝c₁＝1，c_n+1＝a_n+1﹣a_n ， c_n+1＝ $\frac{b_{n}}{b_{n + 2}}$ •c_n（n∈N*）．
（Ⅰ）若数列{b_n}为等比数列，且公比q＞0，且b₁+b₂＝6b₃ ，求q与a_n的通项公式；

（Ⅱ）若数列{b_n}为等差数列，且公差d＞0，证明：c₁+c₂+…+c_n＜1+ $\frac{1}{d}$ ．

查看试题解析
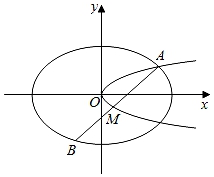
21. 如图，已知椭圆C₁： $\frac{x^{2}}{2}$ +y²＝1，抛物线C₂：y²＝2px（p＞0），点A是椭圆C₁与抛物线C₂的交点，过点A的直线l交椭圆C₁于点B，交抛物线C₂于M（B，M不同于A）．
（Ⅰ）若p＝ $\frac{1}{16}$ ，求抛物线C₂的焦点坐标；
（Ⅱ）若存在不过原点的直线l使M为线段AB的中点，求p的最大值．

查看试题解析
22. 已知1＜a≤2，函数f（x）＝e^x﹣x﹣a，其中e＝2.71828…为自然对数的底数．
（Ⅰ）证明：函数y＝f（x）在（0，+∞）上有唯一零点；

（Ⅱ）记x₀为函数y＝f（x）在（0，+∞）上的零点，证明：

（ⅰ） $\sqrt{a - 1}$ ≤x₀≤ $\sqrt{2 (a - 1)}$ ；

（ⅱ）x₀f（ $e^{x_{0}}$ ）≥（e﹣1）（a﹣1）a．

查看试题解析