初中数学浙教版九年级上册第一章 二次函数 单元检测(提高篇)
试卷更新日期:2020-07-12 类型:单元试卷
一、单选题
-
1. 如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是(
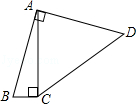 A、y= B、 y= C、 y= D、y=2. 二次函数 ( )的图象如图所示,分析下列四个结论:① ;② ;③ ;④ .其中正确的结论有( )
A、y= B、 y= C、 y= D、y=2. 二次函数 ( )的图象如图所示,分析下列四个结论:① ;② ;③ ;④ .其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个3. 如图,在正方形ABCD中,AB= ,P为对角线AC上的动点,PQ⊥AC交折线A﹣D﹣C于点Q,设AP=x,△APQ的面积为y,则y与x的函数图象正确的是( )
A、1个 B、2个 C、3个 D、4个3. 如图,在正方形ABCD中,AB= ,P为对角线AC上的动点,PQ⊥AC交折线A﹣D﹣C于点Q,设AP=x,△APQ的面积为y,则y与x的函数图象正确的是( )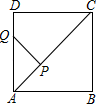 A、
A、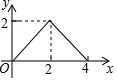 B、
B、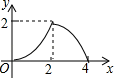 C、
C、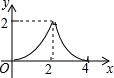 D、
D、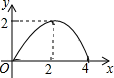 4. 已知函数 ,则使y=k成立的x值恰好有三个,则k的值为( )A、0 B、1 C、2 D、35. 已知二次函数 ( 为常数,且 )的图像过点 , ,若 的长不小于2,则 的取值范围是( )A、 B、 C、 D、6. 对于代数式 ,下列说法正确的是( )
4. 已知函数 ,则使y=k成立的x值恰好有三个,则k的值为( )A、0 B、1 C、2 D、35. 已知二次函数 ( 为常数,且 )的图像过点 , ,若 的长不小于2,则 的取值范围是( )A、 B、 C、 D、6. 对于代数式 ,下列说法正确的是( )①如果存在两个实数p≠q,使得ap2+bp+c=aq2+bq+c,则 ②存在三个实数m≠n≠s,使得am2+bm+c=an2+bn+c=as2+bs+c③如果ac<0,则一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c④如果ac>0,则一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c
A、① B、③ C、②④ D、①③7. 如果我们把函数 称为二次函数 的“镜子函数”,那么对于二次函数 : 的“镜子函数” : ,下列说法:① 的图像关于y轴对称;② 有最小值,最小值为 ;③当方程 有两个不相等的实数根时, ;④直线 与 的图像有三个交点时, 中,正确的有( )A、1个 B、2个 C、3个 D、4个8. 如图,若抛物线y=x2-2x与x轴正半轴相交于点A,点P是y轴上一动点,过点P作直线l∥x轴,与抛物线相交于B,C两点(B在C的左侧),过点C作CD⊥x轴于点D,连接AB、DP,若OC将四边形BADP的面积分成2:1的两部分,则OC的解析式为( ) A、y=x B、y=2x C、y=4x D、y=8x9. 已知抛物线 与y轴交于点A , 与直线 (k为任意实数)相交于B , C两点,则下列结论错误的是( )A、存在实数k , 使得 为等腰三角形 B、存在实数k , 使得 的内角中有两角分别为30°和60° C、任意实数k , 使得 都为直角三角形 D、存在实数k , 使得 为等边三角形10. 定义符号min{a,b}的含义为:当a≥b时min{a,b}=b;当a<b时min{a,b}=a .如min{1,-3}=-3, min{-4,-2}=-4 ,则min{-x2+1,-x}的最大值是( )
A、y=x B、y=2x C、y=4x D、y=8x9. 已知抛物线 与y轴交于点A , 与直线 (k为任意实数)相交于B , C两点,则下列结论错误的是( )A、存在实数k , 使得 为等腰三角形 B、存在实数k , 使得 的内角中有两角分别为30°和60° C、任意实数k , 使得 都为直角三角形 D、存在实数k , 使得 为等边三角形10. 定义符号min{a,b}的含义为:当a≥b时min{a,b}=b;当a<b时min{a,b}=a .如min{1,-3}=-3, min{-4,-2}=-4 ,则min{-x2+1,-x}的最大值是( )
A、 B、 C、1 D、0二、填空题
-
11. 抛物线y=2x²-8x+6与x轴交于点A、B,把抛物线在x轴及其下方的部分记为C1 , 将C1向右平移得到C2 , C2与x轴交于点B、D,若直线y=-x+m与C1、C2共有3个不同的交点,则m的取值范围是。
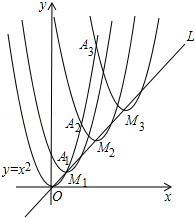
 12. 如图,抛物线y=x2在第一象限内经过的整数点(横坐标,纵坐标都为整数的点)依次为A1 , A2 , A3 , …An , ….将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:
12. 如图,抛物线y=x2在第一象限内经过的整数点(横坐标,纵坐标都为整数的点)依次为A1 , A2 , A3 , …An , ….将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:①抛物线的顶点M1 , M2 , M3 , …Mn , …都在直线L:y=x上;
②抛物线依次经过点A1 , A2 , A3…An , ….
则M2016顶点的坐标为 .
 13. 如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1 , 它与x轴交于两点O,A;将C1绕点A旋转180°得到C2 , 交x轴于A1;将C2绕点A1旋转180°得到C3 , 交x轴于点A2 . .....如此进行下去,直至得到C2018 , 若点P(4035,m)在第2018段抛物线上,则m的值为 .
13. 如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1 , 它与x轴交于两点O,A;将C1绕点A旋转180°得到C2 , 交x轴于A1;将C2绕点A1旋转180°得到C3 , 交x轴于点A2 . .....如此进行下去,直至得到C2018 , 若点P(4035,m)在第2018段抛物线上,则m的值为 .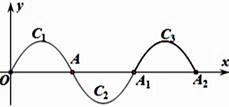 14. 如图,在平面直角坐标系中抛物线y=x2-3x+2与x轴交于A、B两点,与y轴交于点C,D是对称轴右侧抛物线上一点,且tan∠DCB=3,则点D的坐标为。
14. 如图,在平面直角坐标系中抛物线y=x2-3x+2与x轴交于A、B两点,与y轴交于点C,D是对称轴右侧抛物线上一点,且tan∠DCB=3,则点D的坐标为。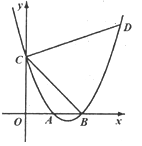 15. 在平面直角坐标系中,函数y=-x+3a+2(a≠0)和y=x2-ax的图象相交于P,Q两点若P,Q都在x轴的上方,则实数a的取值范围是 。
15. 在平面直角坐标系中,函数y=-x+3a+2(a≠0)和y=x2-ax的图象相交于P,Q两点若P,Q都在x轴的上方,则实数a的取值范围是 。
16. 已知抛物线 与 轴相交于A,B两点,其顶点为M,将此抛物线在 轴下方的部分沿 轴翻折,其余部分保持不变,得到一个新的图像,如图,当直线 与此图像有且只有两个公共点时,则 的取值范围为.
三、综合题
-
17. 已知抛物线L:y= x2+ x+c经过点M(2,0),现将抛物线L沿x轴翻折,并向左平移1个单位长度后得到抛物线L1。(1)、求抛物线L1的解析式.(2)、若抛物线L与x轴交于A,B两点(点B在点A右侧),点E在抛物线L1对称轴上一点,O为坐标原点,则抛物线L上是否存在点P,使以A,O,E,P为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由。18. 已知抛物线c:y=-x2-2x+3和直线l:y= x+d。将抛物线c在x轴上方的部分沿x轴翻折180°,其余部分保持不变,翻折后的图象与x轴下方的部分组成一个“M”型的新图象(即新函数m:y=-|x2+2x-3|的图象)。
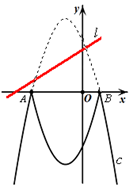 (1)、当直线l与这个新图象有且只有一个公共点时,d=;(2)、当直线l与这个新图象有且只有三个公共点时,求d的值;(3)、当直线l与这个新图象有且只有两个公共点时,求d的取值范围;(4)、当直线l与这个新图象有四个公共点时,直接写出d的取值范围.19. 在平面直角坐标系中,Rt△AOB的位置如图所示,已知∠AOB=90°,AO=BO,点A的坐标为(﹣3,1).
(1)、当直线l与这个新图象有且只有一个公共点时,d=;(2)、当直线l与这个新图象有且只有三个公共点时,求d的值;(3)、当直线l与这个新图象有且只有两个公共点时,求d的取值范围;(4)、当直线l与这个新图象有四个公共点时,直接写出d的取值范围.19. 在平面直角坐标系中,Rt△AOB的位置如图所示,已知∠AOB=90°,AO=BO,点A的坐标为(﹣3,1). (1)、求点B的坐标;(2)、求过A、O、B三点的抛物线的解析式;(3)、设点P为抛物线上到x轴的距离为1的点,点B关于抛物线的对称轴l的对称点为B1 , 求点P的坐标和△B1PB的面积.20. 如图,抛物线 与 x 轴交于点 A、B,与 y 轴交于点 C,且 OC=2OB, 点 D 为线段 OB 上一动点(不与点 B 重合),过点 D 作矩形 DEFH,点 H、F 在抛物线上,点 E 在 x 轴 上.
(1)、求点B的坐标;(2)、求过A、O、B三点的抛物线的解析式;(3)、设点P为抛物线上到x轴的距离为1的点,点B关于抛物线的对称轴l的对称点为B1 , 求点P的坐标和△B1PB的面积.20. 如图,抛物线 与 x 轴交于点 A、B,与 y 轴交于点 C,且 OC=2OB, 点 D 为线段 OB 上一动点(不与点 B 重合),过点 D 作矩形 DEFH,点 H、F 在抛物线上,点 E 在 x 轴 上.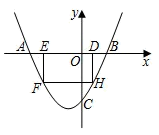 (1)、求抛物线的解析式;(2)、当矩形 DEFH 的周长最大时,求矩形 DEFH 的面积;(3)、在(2)的条件下,矩形 DEFH 不动,将抛物线沿着 x 轴向左平移 m 个单位,抛物线与矩形 DEFH的边交于点 M、N,连接 M、N.若 MN 恰好平分矩形 DEFH 的面积,求 m 的值.21. 某超市拟于中秋节前 天里销售某品牌月饼,其进价为 元/ .设第 天的销售价格为 (元/ ),销售量为 .该超市根据以往的销售经验得出以下的销售规律:①当 时, ;当 时, 与 满足一次函数关系,且当 时, ; 时, .② 与 的关系为 .(1)、当 时, 与 的关系式为;(2)、 为多少时,当天的销售利润 (元)最大?最大利润为多少?(3)、若超市希望第 天到第 天的日销售利润 (元)随 的增大而增大,则需要在当天销售价格的基础上涨 元/ ,求 的最小值.22. 如图,已知二次函数图象的顶点坐标为A(1,9),与坐标轴交于B、C、D三点,且B点的坐标为(-2,0)
(1)、求抛物线的解析式;(2)、当矩形 DEFH 的周长最大时,求矩形 DEFH 的面积;(3)、在(2)的条件下,矩形 DEFH 不动,将抛物线沿着 x 轴向左平移 m 个单位,抛物线与矩形 DEFH的边交于点 M、N,连接 M、N.若 MN 恰好平分矩形 DEFH 的面积,求 m 的值.21. 某超市拟于中秋节前 天里销售某品牌月饼,其进价为 元/ .设第 天的销售价格为 (元/ ),销售量为 .该超市根据以往的销售经验得出以下的销售规律:①当 时, ;当 时, 与 满足一次函数关系,且当 时, ; 时, .② 与 的关系为 .(1)、当 时, 与 的关系式为;(2)、 为多少时,当天的销售利润 (元)最大?最大利润为多少?(3)、若超市希望第 天到第 天的日销售利润 (元)随 的增大而增大,则需要在当天销售价格的基础上涨 元/ ,求 的最小值.22. 如图,已知二次函数图象的顶点坐标为A(1,9),与坐标轴交于B、C、D三点,且B点的坐标为(-2,0)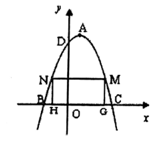
 (1)、求二次函数的解析式;(2)、在二次函数图象位于x轴上方部分有两个动点M、M,且点N在点M的左侧,过M、N作x轴的垂线交x轴于点G、H两点,当四边形MNG为矩形时,求该矩形周长的最大值;(3)、在(2)中的矩形周长最大时,连接BM,已知点P是x轴上一动点,过点P作PQ∥y轴,交直线BM于点Q,是否存在这样的点P,使直线PQ把△BCM分成面积为1:2的两部分?若存在,求出该点的坐标;若不存在,请说明理由。
(1)、求二次函数的解析式;(2)、在二次函数图象位于x轴上方部分有两个动点M、M,且点N在点M的左侧,过M、N作x轴的垂线交x轴于点G、H两点,当四边形MNG为矩形时,求该矩形周长的最大值;(3)、在(2)中的矩形周长最大时,连接BM,已知点P是x轴上一动点,过点P作PQ∥y轴,交直线BM于点Q,是否存在这样的点P,使直线PQ把△BCM分成面积为1:2的两部分?若存在,求出该点的坐标;若不存在,请说明理由。