浙教版2019-2020学年初中数学八年级下学期期末复习专题6 反比例函数
试卷更新日期:2020-07-12 类型:复习试卷
一、单选题
-
1. 下列函数中,是 关于 的反比例函数的是( ).A、 B、 C、 D、2. 函数 的自变量 的取值范围是( )A、 B、 C、 D、3. 若点A(﹣3, ),B(﹣2, ),C(1, )都在反比例函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、4. 关于反比例函数y=
 图象,下列说法正确的是( ) A、必经过点(1,1) B、两个分支分布在第二、四象限 C、两个分支关于x轴成轴对称 D、两个分支关于原点成中心对称5. 如图,点 是反比例函数 的图象上任意一点, 轴交反比例函数 的图象于点B,以AB为边作 ,其中C,D在x轴上,则 为( )
图象,下列说法正确的是( ) A、必经过点(1,1) B、两个分支分布在第二、四象限 C、两个分支关于x轴成轴对称 D、两个分支关于原点成中心对称5. 如图,点 是反比例函数 的图象上任意一点, 轴交反比例函数 的图象于点B,以AB为边作 ,其中C,D在x轴上,则 为( )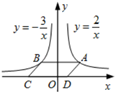 A、2.5 B、3.5 C、4 D、56. 反比例函数 与一次函数y=k(x+1)(其中 x 为自变量,k 为常数)在同一坐标中的图像可能是( )A、
A、2.5 B、3.5 C、4 D、56. 反比例函数 与一次函数y=k(x+1)(其中 x 为自变量,k 为常数)在同一坐标中的图像可能是( )A、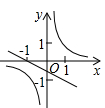 B、
B、 C、
C、 D、
D、 7. 如果反比例函数的图象经过点(3,2),那么下列各点中在此函数图象上的点是( )A、(- ,3 ) B、(9, ) C、(- ,2 ) D、(6, )8. 对于反比例函数 ,下列说法正确的个数是( )
7. 如果反比例函数的图象经过点(3,2),那么下列各点中在此函数图象上的点是( )A、(- ,3 ) B、(9, ) C、(- ,2 ) D、(6, )8. 对于反比例函数 ,下列说法正确的个数是( )①函数图象位于第一、三象限;②函数值 y 随 x 的增大而减小;③若 A(-1, ),B(2, ),C(1, )是图象上三个点,则 < < ;④P 为图象上任一点,过 P 作 PQ⊥y 轴于点 Q,则△OPQ 的面积是定值( )
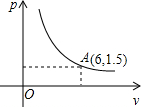
A、1 个 B、2 个 C、3 个 D、4 个9. 下列各点中,同时在直线y=-3x+7和双曲线y= 上的点为( )A、(-3,16) B、(0,7) C、(1,-6) D、(3,-2)10. 在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度 (单位: )与体积 (单位: )满足函数关系式 ( 为常数, ),其图象如图所示,则 的值为()
A、 B、
B、 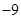 C、 4
D、
C、 4
D、 
二、填空题
-
11. 已知函数 是反比例函数,则m的值为 .12. 如图,点A在双曲线y= 的第一象限的那一支上,AB⊥y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为 ,则k的值为.
 13. 已知点A(3,a)、B(-1,b)在函数 的图像上,那么ab(填“>”或“=”或“<”)14. 已知,反比例函数y= 的图象在第二、四象限内,则k的值可以是 。(写出一个满足条件的k的值即可)15. 某水池容积为300m3 , 原有水100m3 , 现以xm3/min的速度匀速向水池中注水,注满水需要y min,则y关于x的函数表达式为 .16. 已知一次函数y=ax+b,反比例函数y= (a,b,k是常数,且ak≠0),若其中一部分x,y的对应值如下表,则不等式-8<ax+b< 的解集是 .
13. 已知点A(3,a)、B(-1,b)在函数 的图像上,那么ab(填“>”或“=”或“<”)14. 已知,反比例函数y= 的图象在第二、四象限内,则k的值可以是 。(写出一个满足条件的k的值即可)15. 某水池容积为300m3 , 原有水100m3 , 现以xm3/min的速度匀速向水池中注水,注满水需要y min,则y关于x的函数表达式为 .16. 已知一次函数y=ax+b,反比例函数y= (a,b,k是常数,且ak≠0),若其中一部分x,y的对应值如下表,则不等式-8<ax+b< 的解集是 .x
-4
-2
-1
1
2
4
y=ax+b
-6
-4
-3
-1
0
2
y=
-2
-4
-8
8
4
2
三、综合题
-
17. 已知x与y成反比例,且当x= 时,y=(1)、求y关于x的函数表达式(2)、当x= 时,y的值是多少?18. 小林为探索函数 的图象与性经历了如下过程
 (1)、列表:根据表中 的取值,求出对应的 值,将空白处填写完整
(1)、列表:根据表中 的取值,求出对应的 值,将空白处填写完整2.5
3
3.5
4
4.5
5
6
2
1.2
1
(2)、以表中各组对应值为点的坐标,在平面直角坐标系中描点并画出函数图象.(3)、若函数 的图象与 的图象交于点 , ,且 为正整数),则 的值是 .19. 已知反比例函数的图象过点 .(1)、求这个反比例函数的表达式;(2)、这个函数的图象分布在哪些象限? 随 的增大如何变化?(3)、点 , 和 是否在这个函数的图象上?20. 已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货.设平均卸货速度为ν(单位:吨/小时),卸完这批货物所需的时间为t(单位:小时)(1)、求v关于t的函数表达式(2)、若要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?21. 如图,已知点A(2,m)是反比例函数y= (k>0,x>0)的图象上一点,过点A作AB⊥x轴于点B,连结OA,△ABO的面积为4. (1)、求k和m的值(2)、直线y= x+n(n<0)与AB的延长线交于点C,与反比例函数图象交于点E。
(1)、求k和m的值(2)、直线y= x+n(n<0)与AB的延长线交于点C,与反比例函数图象交于点E。①若n=-2,求点C坐标
②若点E到直线AB的距离等于AC,求n的值。
22. 如图,奥运圣火抵达某市奥林匹克广场后,沿图中直角坐标系中的一段反比例函数图象传递.动点 表示火炬位置,火炬从离北京路10米处的M点开始传道,到离北京路1000米的N点时传递活动结束.迎圣火临时指挥部设在坐标原点O(北京路与奥运路的十字路口),OATB为少先队员鲜花方阵,方阵始终保持矩形形状且面积恒为10000(路线宽度均不计). (1)、求图中反比例函数的关系式(不需写出自变量的取值范围);(2)、当鲜花方阵的周长为500米时,确定此时火炬的位置(用坐标表示).23. 如图1,在平面直角坐标系xOy中,已知△ABC,∠ABC=90°,顶点A在第一象限内,BC在x轴的正半轴上(B在C的右侧),AB= ,∠ACB=30°,△ADC与△ABC关于AC所在的直线对称,且函数y= (k>0)的图象过点D.
(1)、求图中反比例函数的关系式(不需写出自变量的取值范围);(2)、当鲜花方阵的周长为500米时,确定此时火炬的位置(用坐标表示).23. 如图1,在平面直角坐标系xOy中,已知△ABC,∠ABC=90°,顶点A在第一象限内,BC在x轴的正半轴上(B在C的右侧),AB= ,∠ACB=30°,△ADC与△ABC关于AC所在的直线对称,且函数y= (k>0)的图象过点D. (1)、当OC=2时,求k的值;(2)、如图2,若点A和点D在同一个反比例函数图象上,求OC的长;(3)、在(2)的条件下,点D与点E关于原点成中心对称,x轴上有一点F,平面内有一点G,若D、E、F、G四点构成的四边形是矩形,求F点的坐标.
(1)、当OC=2时,求k的值;(2)、如图2,若点A和点D在同一个反比例函数图象上,求OC的长;(3)、在(2)的条件下,点D与点E关于原点成中心对称,x轴上有一点F,平面内有一点G,若D、E、F、G四点构成的四边形是矩形,求F点的坐标.
24. 阅读理解:已知:对于实数a≥0,b≥0,满足a+b≥2 ,当且仅当a = b时,等号成立,此时取得代数式a+b的最小值.根据以上结论,解决以下问题:
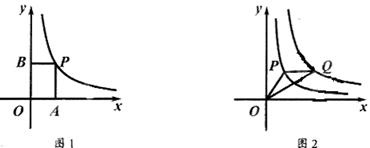 (1)、拓展:若a>0,当且仅当a=时,a+ 有最小值,最小值为;(2)、应用:
(1)、拓展:若a>0,当且仅当a=时,a+ 有最小值,最小值为;(2)、应用:①如图1,已知点P为双曲线y= (x>0)上的任意一点,过点P作PA⊥x轴,PB丄y轴,四边形OAPB的周长取得最小值时,求出点P的坐标以及周长最小值:
②如图2,已知点Q是双曲线y= (x>0)上一点,且PQ∥x轴, 连接OP、OQ,当线段OP取得最小值时,在平面内取一点C,使得以0、P、Q、C为顶点的四边形是平行四边形,求出点C的坐标.