浙教版2019-2020学年初中数学八年级下学期期末复习专题5 特殊平行四边形
试卷更新日期:2020-07-12 类型:复习试卷
一、单选题
-
1. 如图,在长方形钟面示意图中,时钟的中心在长方形对角线的交点上,长方形宽为 40cm , 钟面数字 2 在长方形的顶点处,则长方形的长为( )cm
 A、80 B、60 C、50 D、402. 下列条件中,不能判定平行四边形ABCD为矩形的是( )A、∠A=∠C B、∠A=∠B C、AC=BD D、AB⊥BC3. 如图,在 ABCD中,AB=2 ,AD=4,AC⊥BC,则△DBC比△ABC的周长长( )
A、80 B、60 C、50 D、402. 下列条件中,不能判定平行四边形ABCD为矩形的是( )A、∠A=∠C B、∠A=∠B C、AC=BD D、AB⊥BC3. 如图,在 ABCD中,AB=2 ,AD=4,AC⊥BC,则△DBC比△ABC的周长长( )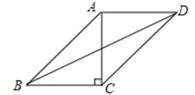 A、2 B、4 C、5 D、4. 在数学活动课上,老师让同学们判定一个四边形门框是否为矩形,下面是某合作小组的四位同学的拟订方案,其中正确的是( )A、测量对角线是否互相平分 B、测量两组对边是否分别相等 C、测量一组对角是否为直角 D、测量两组对边是否相等,再测量对角线是否相等5. 如图,在△ABC中,点D在BC上,DE∥AC,DF∥AB,下列四个判断中错误的是( )
A、2 B、4 C、5 D、4. 在数学活动课上,老师让同学们判定一个四边形门框是否为矩形,下面是某合作小组的四位同学的拟订方案,其中正确的是( )A、测量对角线是否互相平分 B、测量两组对边是否分别相等 C、测量一组对角是否为直角 D、测量两组对边是否相等,再测量对角线是否相等5. 如图,在△ABC中,点D在BC上,DE∥AC,DF∥AB,下列四个判断中错误的是( ) A、四边形AEDF是平行四边形 B、若∠BAC=90°,则四边形AEDF是矩形 C、若AD平分∠BAC,则四边形AEDF是矩形 D、若AD⊥BC且AB=AC,则四边形AEDF是菱形6. 如图,在菱形ABCD中,P、Q分别是AD、AC的中点,如果 ,那么菱形ABCD的周长是( )
A、四边形AEDF是平行四边形 B、若∠BAC=90°,则四边形AEDF是矩形 C、若AD平分∠BAC,则四边形AEDF是矩形 D、若AD⊥BC且AB=AC,则四边形AEDF是菱形6. 如图,在菱形ABCD中,P、Q分别是AD、AC的中点,如果 ,那么菱形ABCD的周长是( )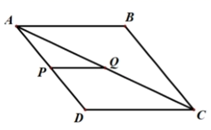 A、16 B、8 C、4 D、27. 菱形具有而矩形不具有的性质是( )A、对边相等 B、对角线互相平分 C、对角线互相垂直 D、对角线相等8. 如图,在一张平行四边形纸片ABCD中,画一个菱形,甲、乙两位同学的画法如下:
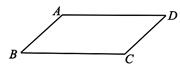
A、16 B、8 C、4 D、27. 菱形具有而矩形不具有的性质是( )A、对边相等 B、对角线互相平分 C、对角线互相垂直 D、对角线相等8. 如图,在一张平行四边形纸片ABCD中,画一个菱形,甲、乙两位同学的画法如下:甲:以B , A为圆心,AB长为半径作弧,分别交BC , AD于点E , F , 则四边形ABEF为菱形;乙:作∠A , ∠B的平分线AE , BF , 分别交BC于点E , 交AD于点F , 则四边形ABEF是菱形;关于甲、乙两人的画法,下列判断正确的是( )
 A、仅甲正确 B、仅乙正确 C、甲、乙均正确 D、甲、乙均错误9. 下列说法不能判断是正方形的是( )A、对角线互相垂直且相等的平行四边形 B、对角线互相垂直的矩形 C、对角线相等的菱形 D、对角线互相垂直平分的四边形10. 一个大矩形按如图方式分割成16个小矩形,且只有标号为①②③的三个大小不同的小矩形为正方形,在满足条件的所有分割中,若知道16个小矩形中n个小矩形的周长,就一定能算出这个大矩形的面积,则n的最小值是( )
A、仅甲正确 B、仅乙正确 C、甲、乙均正确 D、甲、乙均错误9. 下列说法不能判断是正方形的是( )A、对角线互相垂直且相等的平行四边形 B、对角线互相垂直的矩形 C、对角线相等的菱形 D、对角线互相垂直平分的四边形10. 一个大矩形按如图方式分割成16个小矩形,且只有标号为①②③的三个大小不同的小矩形为正方形,在满足条件的所有分割中,若知道16个小矩形中n个小矩形的周长,就一定能算出这个大矩形的面积,则n的最小值是( )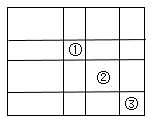 A、3 B、4 C、5 D、611. 如图,四边形ABCD是正方形,直线L1、L2、L3 , 若L1与L2的距离为5,L2与L3的距离7,则正方形ABCD的面积等于( )
A、3 B、4 C、5 D、611. 如图,四边形ABCD是正方形,直线L1、L2、L3 , 若L1与L2的距离为5,L2与L3的距离7,则正方形ABCD的面积等于( )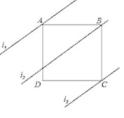 A、70 B、74 C、144 D、14812. 如图,将n个边长都为2的正方形按如图所示摆放,点A1、A2、A3 , …,An分别是正方形的中心,则这n个正方形重叠的面积之和是( )
A、70 B、74 C、144 D、14812. 如图,将n个边长都为2的正方形按如图所示摆放,点A1、A2、A3 , …,An分别是正方形的中心,则这n个正方形重叠的面积之和是( )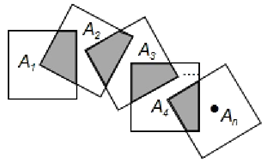 A、n B、n-1 C、4n D、4(n-1)
A、n B、n-1 C、4n D、4(n-1)二、填空题
-
13. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,P为AB边上不与A,B重合的一动点,过点P分别作PE⊥AC于点E,PF⊥BC于点F,则线段EF的最小值是 .
 14. 如图所示,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为.
14. 如图所示,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为.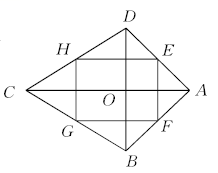 15. 矩形 中, , ,点E、点F在直线AD上,且四边形BCFE为菱形,若点M为线段EF的中点,则线段AM的长为 .16. 菱形的面积为24,一条对角线长为6,则它的周长是.17. 如图,正方形ABCD的对角线长为8,E为AB上一点,若EF⊥AC于点F,EG⊥BD于点G,则EF+EG=.
15. 矩形 中, , ,点E、点F在直线AD上,且四边形BCFE为菱形,若点M为线段EF的中点,则线段AM的长为 .16. 菱形的面积为24,一条对角线长为6,则它的周长是.17. 如图,正方形ABCD的对角线长为8,E为AB上一点,若EF⊥AC于点F,EG⊥BD于点G,则EF+EG=.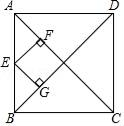 18. 小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得 ,接着活动学具成为图2所示正方形,并测得正方形的对角线 ,则图1中对角线AC的长为 .
18. 小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得 ,接着活动学具成为图2所示正方形,并测得正方形的对角线 ,则图1中对角线AC的长为 .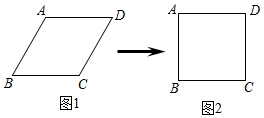
三、解答题
-
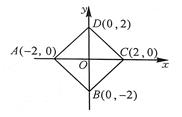
19. 如图,在平面直角坐标系中,四边形ABCD的顶点坐标分别是A(-2,0)、B(0,-2)、C(2,0)、D(0,2),求证:四边形ABCD是正方形.
 20. 如图,在平行四边形ABCD中,AQ、BN、CN、DQ分別是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AQ与BN相交于点P,CN与DQ相交于点M,判断四边形MNPQ的形状,并证明你的结论.
20. 如图,在平行四边形ABCD中,AQ、BN、CN、DQ分別是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AQ与BN相交于点P,CN与DQ相交于点M,判断四边形MNPQ的形状,并证明你的结论.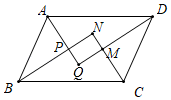 21. 如图,在正方形方格纸中,线段AB的两个端点和点P都在小方格的格点上,分别按下列要求画格点四边形.
21. 如图,在正方形方格纸中,线段AB的两个端点和点P都在小方格的格点上,分别按下列要求画格点四边形.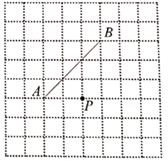 (1)、在图甲中画一个以AB为边的平行四边形,使点P落在AB的对边上(不包括端点).(2)、在图乙中画一个以AB为对角线的菱形,使点P落在菱形的内部(不包括边界).
(1)、在图甲中画一个以AB为边的平行四边形,使点P落在AB的对边上(不包括端点).(2)、在图乙中画一个以AB为对角线的菱形,使点P落在菱形的内部(不包括边界).(注:图甲、图乙在答卷纸上)
22. 如图,已知在矩形ABCD中,AB=8,AD=6,点E、F分别在边CD、AB上,且DE=BF. (1)、 求证:四边形AFCE是平行四边形;(2)、若▱AFCE是菱形,求菱形AFCE的周长.23. 如图,在▱ABCD中,AC=8,BD=12,点E、F在对角线BD上,点E从点B出发以1个单位每秒的速度向点D运动,同时点F从点D出发以相同速度向点B运动,到端点时运动停止,运动时间为t秒.
(1)、 求证:四边形AFCE是平行四边形;(2)、若▱AFCE是菱形,求菱形AFCE的周长.23. 如图,在▱ABCD中,AC=8,BD=12,点E、F在对角线BD上,点E从点B出发以1个单位每秒的速度向点D运动,同时点F从点D出发以相同速度向点B运动,到端点时运动停止,运动时间为t秒.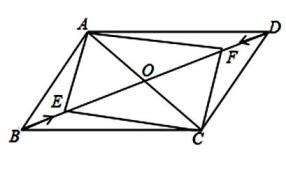 (1)、求证:四边形AECF为平行四边形.(2)、求t为何值时,四边形AECF为矩形.24. 我们给出如下定义:把对角线互相垂直的四边形叫做“正交四边形”.
(1)、求证:四边形AECF为平行四边形.(2)、求t为何值时,四边形AECF为矩形.24. 我们给出如下定义:把对角线互相垂直的四边形叫做“正交四边形”.如图1,在四边形 中, ,四边形 就是“正交四边形”.
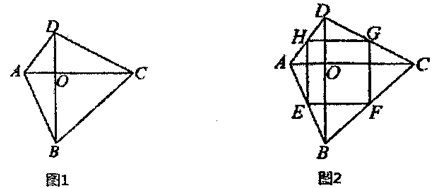 (1)、下列四边形,一定是“正交四边形”的是.
(1)、下列四边形,一定是“正交四边形”的是.①平行四边形②矩形③菱形④正方形
(2)、如图2,在“正交四边形” 中,点 分别是边 的中点,求证:四边形 是矩形.(3)、小明说:“计算‘正交四边形’的面积可以仿照菱形的方法,面积是对角线之积的一半.”小明的说法正确吗?如果正确,请给出证明;如果不正确,请给出反例.25. 已知,如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,动点P在线段BC上以每秒2个单位长的速度由点C向B 运动.设 动点P的运动时间为t秒.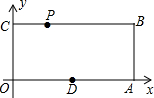
 (1)、当t为何值时,四边形PODB是平行四边形;(2)、在直线CB上是否存在一点Q,使得O、D、Q、P四点为顶点的四边形是菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由;(3)、在线段PB上有一点M,且PM=5,当P运动 ▲ 秒时,四边形OAMP的周长最小, 并画图标出点M的位置.26. 如图,等腰△ABC中,已知AC=BC=2 , AB=4,作∠ACB的外角平分线CF,点E从点B沿着射线BA以每秒2个单位的速度运动,过点E作BC的平行线交CF于点F.
(1)、当t为何值时,四边形PODB是平行四边形;(2)、在直线CB上是否存在一点Q,使得O、D、Q、P四点为顶点的四边形是菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由;(3)、在线段PB上有一点M,且PM=5,当P运动 ▲ 秒时,四边形OAMP的周长最小, 并画图标出点M的位置.26. 如图,等腰△ABC中,已知AC=BC=2 , AB=4,作∠ACB的外角平分线CF,点E从点B沿着射线BA以每秒2个单位的速度运动,过点E作BC的平行线交CF于点F. (1)、求证:四边形BCFE是平行四边形;(2)、当点E是边AB的中点时,连接AF,试判断四边形AECF的形状,并说明理由;(3)、设运动时间为t秒,是否存在t的值,使得以△EFC的其中两边为邻边所构造的平行四边形恰好是菱形?不存在的,试说明理由;存在的,请直接写出t的值.答:t= .
(1)、求证:四边形BCFE是平行四边形;(2)、当点E是边AB的中点时,连接AF,试判断四边形AECF的形状,并说明理由;(3)、设运动时间为t秒,是否存在t的值,使得以△EFC的其中两边为邻边所构造的平行四边形恰好是菱形?不存在的,试说明理由;存在的,请直接写出t的值.答:t= .