浙教版2019-2020学年初中数学八年级下学期期末复习专题4 平行四边形
试卷更新日期:2020-07-12 类型:复习试卷
一、单选题
-
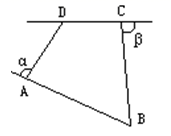
1. 如图,在四边形ABCD中,∠α、∠β分别是与∠BAD、∠BCD相邻的补角,且∠B+∠CDA=140°,则∠α+∠β=( ).
 A、260° B、150° C、135° D、140°2. 内角和为540°的多边形是( )A、三角形 B、四边形 C、五边形 D、六边形3. 七边形的对角线总共有( )A、12条 B、13条 C、14条 D、15条4. 如图,▱ABCD的对角线AC、BD相交于点O , 且AC+BD=24.若△OAB的周长是20,则AB的长为( )
A、260° B、150° C、135° D、140°2. 内角和为540°的多边形是( )A、三角形 B、四边形 C、五边形 D、六边形3. 七边形的对角线总共有( )A、12条 B、13条 C、14条 D、15条4. 如图,▱ABCD的对角线AC、BD相交于点O , 且AC+BD=24.若△OAB的周长是20,则AB的长为( )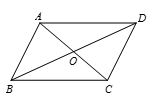 A、8 B、9 C、10 D、125. 若平行四边形的周长为120cm,相邻两边长度之比为5:7,那么较长的边长为( )A、35 cm B、28cm C、42 cm D、25 cm6. 下列图案中,是中心对称图形的是( )A、
A、8 B、9 C、10 D、125. 若平行四边形的周长为120cm,相邻两边长度之比为5:7,那么较长的边长为( )A、35 cm B、28cm C、42 cm D、25 cm6. 下列图案中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
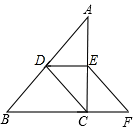
D、 7. 在四边形ABCD中,AB∥CD,再添加下列其中一个条件后,四边形ABCD不一定是平行四边形的是( )A、AB=CD B、AD=BC C、AD∥BC D、∠A=∠C8. 如图,在平行四边形ABCD中,EF∥AD , GH∥AB , 则图中的平行四边形的个数共有( )个.
7. 在四边形ABCD中,AB∥CD,再添加下列其中一个条件后,四边形ABCD不一定是平行四边形的是( )A、AB=CD B、AD=BC C、AD∥BC D、∠A=∠C8. 如图,在平行四边形ABCD中,EF∥AD , GH∥AB , 则图中的平行四边形的个数共有( )个. A、12个 B、9个 C、5个 D、7个9. 下面给出的四边形ABCD中,∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的条件是( )A、3∶4∶3∶4 B、3∶3∶4∶4 C、2∶3∶4∶5 D、3∶4∶4∶310. 如图,在 ABCD中,对角经AC,BD交于点O,BD=2AD,点E,F,G分别是OA,OB,CD的中点,EG交FD于点H。有下列4个结论:①ED⊥CA;②EF=EG;③FH= FD;④S△EFD= S△CED , 其中说法正确的有( )
A、12个 B、9个 C、5个 D、7个9. 下面给出的四边形ABCD中,∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的条件是( )A、3∶4∶3∶4 B、3∶3∶4∶4 C、2∶3∶4∶5 D、3∶4∶4∶310. 如图,在 ABCD中,对角经AC,BD交于点O,BD=2AD,点E,F,G分别是OA,OB,CD的中点,EG交FD于点H。有下列4个结论:①ED⊥CA;②EF=EG;③FH= FD;④S△EFD= S△CED , 其中说法正确的有( ) A、1个 B、2个 C、3个 D、4个11. 用反证法证明命题“在三角形中,至多有一个内角是直角”时,应先假设( )A、至多有两个内角是直角 B、至少有一个内角是直角 C、至多有一个内角是直角 D、至少有两个内角是直角12. 如图,∠A=∠B=∠C=∠D=∠E=∠F=60°,AB=3,BC=DE=1,CD=2,EF=0.5,则AG的长是( )
A、1个 B、2个 C、3个 D、4个11. 用反证法证明命题“在三角形中,至多有一个内角是直角”时,应先假设( )A、至多有两个内角是直角 B、至少有一个内角是直角 C、至多有一个内角是直角 D、至少有两个内角是直角12. 如图,∠A=∠B=∠C=∠D=∠E=∠F=60°,AB=3,BC=DE=1,CD=2,EF=0.5,则AG的长是( ) A、5.5 B、6 C、6.5 D、7
A、5.5 B、6 C、6.5 D、7二、填空题
-
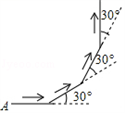
13. 若点P(﹣2,b)与点M(a,3)关于原点对称,则a+b= .14. 如图,小新从A点出发,沿直线前进50米后向左转30°,再沿直线前进50米,又向左转30°,…照这样下去,小新第一次回到出发地A点时,一共走了米.
 15. 在平行四边形ABCD中,若 与 的度数之比为 ,则 的度数为 .16. 如图,在▱ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连结OE.若∠ABC=60,∠BAC=80°,则∠1的度数为 .
15. 在平行四边形ABCD中,若 与 的度数之比为 ,则 的度数为 .16. 如图,在▱ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连结OE.若∠ABC=60,∠BAC=80°,则∠1的度数为 . 17. 用反证法证明命题“在直角三角形中,至少有一个锐角不大于 45°”时第一步先假设所求证的结论不成立,即问题表述为.18. 如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有次.
17. 用反证法证明命题“在直角三角形中,至少有一个锐角不大于 45°”时第一步先假设所求证的结论不成立,即问题表述为.18. 如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有次.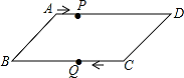
三、解答题
-
19. 如图,已知四边形ABCD和点O,求作一个四边形A’B’C’D’与四边形ABCD关于点O成中心对称.(不写作法,保留作图痕迹)
 20. 如图,五边形ABCDE的每个内角都相等,已知EF⊥BC,求证:EF平分∠AED。
20. 如图,五边形ABCDE的每个内角都相等,已知EF⊥BC,求证:EF平分∠AED。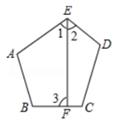 21. 如图,已知E,F分别是 ABCD的边CD,AB上的点,且DE=BF。求证:AE∥CF。
21. 如图,已知E,F分别是 ABCD的边CD,AB上的点,且DE=BF。求证:AE∥CF。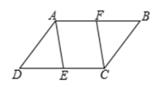 22. 如图7,已知平行四边形ABCD的周长是32cm,AB︰BC=5︰3,AE⊥BC,垂足为E,AF⊥CD,垂足为F,∠EAF=2∠C.
22. 如图7,已知平行四边形ABCD的周长是32cm,AB︰BC=5︰3,AE⊥BC,垂足为E,AF⊥CD,垂足为F,∠EAF=2∠C. (1)、求∠C的度数;(2)、已知DF的长是关于 的方程 - -6=0的一个根,求该方程的另一个根.
(1)、求∠C的度数;(2)、已知DF的长是关于 的方程 - -6=0的一个根,求该方程的另一个根.