浙教版2019-2020学年初中数学八年级下学期期末复习专题2 一元二次方程

试卷更新日期：2020-07-12 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列方程是一元二次方程的是 $($ $)$

A、 $- 6 x + 2 = 0$ B、 $2 x^{2} - y + 1 = 0$ C、 $x^{2} + 2 x = 0$ D、 $\frac{1}{x^{2}} + x = 2$

查看试题解析
2. 如果关于x的一元二次方程（m+1）x²+x+m²﹣2m﹣3＝0有一个根为0，则m的值（　　）

A、﹣1 B、3 C、﹣1或3 D、以上答案都不对

查看试题解析
3. 将方程x(x-2)=x+3化成一般形式后，二次项系数和常数项分别为（）

A、-3，3 B、-1，-3 C、1，3 D、1，-3

查看试题解析
4. 一元二次方程2x²＋6x＋3= 0 经过配方后可变形为（）

A、 ${(x + 3)}^{2}$ =6 B、 ${(x - 3)}^{2}$ =12 C、 ${(x + \frac{3}{2})}^{2} = \frac{3}{4}$ D、 ${(x - \frac{3}{2})}^{2} = \frac{15}{4}$

查看试题解析
5. 用公式法解方程 $\sqrt{2}$ x²+4 $\sqrt{3}$ x=2 $\sqrt{2}$ ,其中求的Δ的值是（）

A、16 B、 $\pm$ 4 C、 $\sqrt{32}$ D、64

查看试题解析
6. 方程x（x﹣1）＝5（x﹣1）的解是（）

A、1 B、5 C、1或5 D、无解

查看试题解析
7. 如果关于x的方程x²﹣ $\sqrt{k}$ x+1=0有实数根，那么k的取值范围是（）

A、k＞0 B、k≥0 C、k＞4 D、k≥4

查看试题解析
8. 受新冠肺炎疫情影响，某企业生产总值从1月份的300万元，连续两个月降至260万元，设每月平均下降率为x，则可列方程（）

A、 $300 {(1 + x)}^{2} = 260$ B、 $300 (1 - x^{2}) = 260$ C、 $300 (1 - 2 x) = 260$ D、 $300 {(1 - x)}^{2} = 260$

查看试题解析
9. 如图，有一长方形鸡场，鸡场的一边靠墙（墙长 18 米），另三边用竹篱笆围成，竹篱笆的总长为 35 米，与墙平行的边留有 1 米宽的门（门用其它材料做成），若鸡场的面积为 160 平方米，则鸡场与墙垂直的边长为（）

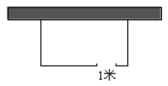A、7.5 米 B、8米 C、10米 D、10米或8米

查看试题解析
10. 若α，β是方程x²﹣2x﹣3＝0的两个实数根，则α²+β²+αβ的值为（　　）

A、10 B、9 C、7 D、5

查看试题解析

二、填空题

11. 关于x的一元二次方程ax²+bx－2020=0有一个根为x=－1，写出一组满足条件的实数a，b的值：a＝， b＝．

查看试题解析
12. 若关于x的一元二次方程 $2 x^{2} + (2 k + 1) x - (4 k - 1) = 0$ 的二次项系数、一次项系数、常数项的和是0，则 $k =$ .

查看试题解析
13. 若2(x-1)²-8=0，则x的值为．

查看试题解析
14. 关于x的一元二次方程(a＋1)x²－2x＋3＝0有实数根，则整数a的最大值是.

查看试题解析
15. 某服装店经销一种品牌服装，平均每天可销售20件，每件赢利44元，经市场预测发现：在每件降价不超过10元的情况下，若每件降价1元，则每天可多销售5件，若该专卖店要使该品牌服装每天的赢利为1600元，则每件应降价____元．

查看试题解析
16. 如图，已知AB⊥BC，AB=12cm，BC=8cm.一动点N从C点出发沿CB方向以1cm/s的速度向B点运动，同时另一动点M由点A沿AB方向以2cm/s的速度也向B点运动，其中一点到达B点时另一点也随之停止，当△MNB的面积为24cm²时运动的时间t为秒.

查看试题解析

三、解答题

17. 已知x₁ ， x₂是关于x的方程x²﹣kx+5（k﹣5）＝0的两个正实数根，且满足2x₁+x₂＝7，求实数k的值.

查看试题解析
18. 解方程：

(1)、(x+2)²=4(自选方法)

(2)、2x²-x-1=0(配方法)、

(3)、x²-1=4x(公式法)

(4)、x²-1=2x+2(因式分解法)

查看试题解析
19. 已知m是方程 $x^{2} - 3 x = 0$ 的一个根，求 ${(m - 3)}^{2} + (m + 2) (m - 2)$ 的值．

查看试题解析
20. 阅读第（1）题的解题过程，再解答第（2）题：
（ 1 ）例：解方程x²﹣|x|﹣2＝0.

解：当x≥0时，原方程可化为x²﹣x﹣2＝0.

解得：x₁＝2，x₂＝﹣1（不合题意.舍去）

当x＜0时，原方程可化为x²+x﹣2＝0.

解得：x₁＝﹣2，x₂＝1（不合题意.舍去）

∴原方程的解是x₁＝2，x₁＝﹣2.

（ 2 ）请参照上例例题的解法，解方程x²﹣x|x﹣1|﹣1＝0.

查看试题解析
21. 如果关于 $x$ 的一元二次方程 $a x^{2} + b x + c = 0$ 有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“倍根方程”，研究发现了此类方程的一般性结论：设其中一根为 $t$ ，则另一个根为 $2 t$ ，因此 $a x^{2} + b x + c = a (x - t) (x - 2 t) = a x^{2} - 3 a t x + 2 t^{2} a$ ，所以有 $b^{2} - \frac{9}{2} a c = 0$ ；我们记“ $K = b^{2} - \frac{9}{2} a c$ ”即 $K = 0$ 时，方程 $a x^{2} + b x + c = 0$ 为倍根方程；
下面我们根据此结论来解决问题：

(1)、方程① $2 x^{2} - 3 x + 1 = 0$ ；方程② $x^{2} - 2 x - 8 = 0$ ；方程③ $x^{2} + x = - \frac{2}{9}$ 这几个方程中，是倍根方程的是（填序号即可）；

(2)、若 $(x - 1) (m x - n) = 0$ 是倍根方程，则 $\frac{2 n}{m}$ 的值为；

查看试题解析
22. 将 4个数a，b，c，d 排成2 行、2 列，两边各加一条竖直线记成 $|_{b}^{a}$ ${}_{d}^{c}|$ ，定义 $|_{b}^{a}$ ${}_{d}^{c}|$ ＝ad-bc，上述记号就叫做2阶行列式．

(1)、若 $|_{49}^{2 x}$ ${}_{3 x}^{1}|$ ＝0，求x的值；

(2)、若 $|_{1 - x}^{x + 1}$ ${}_{x + 1}^{x - 1}|$ ＝6，求x的值．

查看试题解析
23. 随着粤港澳大湾区建设的加速推进，广东省正加速布局以5G等为代表的战略性新兴产业．据统计，目前广东5G基站的数量约1.5万座，计划到2020年底，全省5G基站数量是目前的4倍，到2022年底，全省5G基站数量将达到17.34万座．

(1)、计划到2020年底，全省5G基站的数量是多少万座？

(2)、按照计划，求2020年底到2022年底，全省5G基站数量的年平均增长率；

(3)、求2021年底全省5G基站的数量．

查看试题解析
24. 如图，在△ABC中，∠B=90°，AB=12cm，BC=16cm．点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动．如果P、Q分别从A、B同时出发，当一个点到达终点时，另一个点也随之停止运动．设运动的时间为t秒．

(1)、当t为何值时，△PBQ的面积等于35cm²？

(2)、当t为何值时，PQ的长度等于8 $\sqrt{2}$ cm？

(3)、若点P，Q的速度保持不变，点P在到达点B后返回点A，点Q在到达点C后返回点B，一个点停止，另一个点也随之停止．问：当t为何值时，△PCQ的面积等于 ${32cm}^{2}$ ？

查看试题解析