浙教版2019-2020学年初中数学七年级下学期期末复习专题4 因式分解

试卷更新日期：2020-07-12 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列各式中，不能分解因式的是（）

A、4x²＋2xy＋ $\frac{1}{4}$ y² B、4x²－2xy＋ $\frac{1}{4}$ y² C、4x²－ $\frac{1}{4}$ y² D、－4x²－ $\frac{1}{4}$ y²

查看试题解析
2. 下列各式从左到右的变形中，属于因式分解的是（）

A、(3-x)(3+x)=9-x² B、(y+1)(y-3)=-(3-y)(y+1) C、4yz-2y²z+z=2y(2z-yz)+z D、-8x²+8x-2=-2(2x-1)²

查看试题解析
3. 下列分解因式中，完全正确的是（）

A、 $x^{3} - x = x (x^{2} - 1)$ B、 $4 a^{2} - 4 a + 1 = 4 a (a - 1) + 1$ C、 $x^{2} + y^{2} = {(x + y)}^{2}$ D、 $6 a - 9 - a^{2} = - {(a - 3)}^{2}$

查看试题解析
4. 下列各组代数式中没有公因式的是（）

A、4a²bc与8abc² B、a³b²+1与a²b³–1 C、b(a–2b)²与a（2b–a）² D、x+1与x²–1

查看试题解析
5. 下列添括号正确是（）

A、 $7 x^{3} - 2 x^{2} - 8 x + 6 = 7 x^{3} - (2 x^{2} - 8 x + 6)$ B、 $a - b + c - d = (a - d) - (b + c)$ C、 $a - 2 b + 7 c = a - (2 b - 7 c)$ D、 $5 a^{2} - 6 a b - 2 a - 3 b = - (5 a^{2} + 6 a b - 2 a) - 3 b$

查看试题解析
6. 若y²+my+9是一个完全平方式，则m的值为（）

A、3 B、±3 C、6 D、±6

查看试题解析
7. 下列多项式哪一项可以用平方差公式分解因式（）

A、 $4 x^{2} + y^{2}$ B、 $a^{2} + 3$ C、 $y^{2} - 4 x^{2}$ D、 $-4 x^{2} - y^{2}$

查看试题解析
8. 下列多项式能直接用完全平方公式进行因式分解的是（）

A、x²+2x﹣1 B、x²﹣x+ $\frac{1}{4}$ C、x²+xy+y² D、9+x²﹣3x

查看试题解析
9. 下列因式分解正确的是（）

A、–4a²+4b²=–4(a²–4b²)=–4(a+2b)(a–2b) B、3m³–12m=3m(m²–4) C、4x⁴y–12x²y²+7=4x²y(x²–3y)+7 D、4–9m²=(2+3m)(2–3m)

查看试题解析
10. 小强是一位密码编译爱好者，在他的密码手册中，有这样一条信息：x﹣y，a﹣b，2，x²﹣y² ， a，x+y，分别对应下列六个字：华、我、爱、美、游、中，现将2a（x²﹣y²）﹣2b（x²﹣y²）因式分解，结果呈现的密码信息可能是（）

A、爱我中华 B、我游中华 C、中华美 D、我爱美

查看试题解析

二、填空题

11. 如果 $(x + 3) (x + a) - 2$ 可以因式分解为 $(x + m) (x + n)$ （其中 $m$ ， $n$ 均为整数），则 $a$ 的值是．

查看试题解析
12. 多项式x²+mx+5因式分解得（x+5）（x+n），则m= ， n= ．

查看试题解析
13. 将–x⁴–3x²+x提取公因式–x后，剩下的因式是.

查看试题解析
14. 多项式 $(x - m) (x - n)$ 的展开结果中的 $x$ 的一次项系数为3，常数项为2，则 $m^{2} n + m n^{2}$ 的值为 .

查看试题解析
15. 多项式 $4 a^{2} + 9$ 加上一个单项式后，可化为一个整式的平方，则这个单项式是.（写一个即可）

查看试题解析
16. 若 $x^{2} + 2 (3 - m) x + 25$ 可以用完全平方式来分解因式，则 $m$ 的值为．

查看试题解析

三、解答题

17. 分解因式：

(1)、a²b－abc；

(2)、x(m+n)-y(m+n)+(m+n)

(3)、9x²-16y²

(4)、3ax²-6axy+3ay²

查看试题解析
18. 数25⁷－5¹²能被120整除吗?请说明理由.

查看试题解析
19. 已知二次三项式x²+px+q的常数项与（x-1）（x-9）的常数项相同，而它的一次项与（x-2）（x-4）的一次项相同，试将此多项式因式分解．

查看试题解析
20.

(1)、因式分解：（x-y）（3x-y）+2x（3x-y）；

(2)、设 y=kx，是否存在实数 k，使得上式的化简结果为 x²？求出所有满足条件的 k 的值．若不能，请说明理由．

查看试题解析
21. 解下列各题：

(1)、分解因式：9a²（x﹣y）+4b²（y﹣x）；

(2)、甲，乙两同学分解因式x²+mx+n，甲看错了n，分解结果为（x+2）（x+4）；乙看错了m，分解结果为（x+1）（x+9），请分析一下m，n的值及正确的分解过程．

查看试题解析
22. 下面是某同学对多项式（x²－4x+2）（x²－4x+6）+4进行因式分解的过程.
解：设x²－4x=y

原式=（y+2）（y+6）+4    （第一步）

= y²+8y+16           （第二步）

=（y+4）²            （第三步）

=（x²－4x+4）²       （第四步）

回答下列问题：

(1)、该同学第二步到第三步运用了因式分解的_______.

A、提取公因式 B、平方差公式 C、两数和的完全平方公式 D、两数差的完全平方公式

(2)、该同学因式分解的结果是否彻底？.（填“彻底”或“不彻底”）
若不彻底，请直接写出因式分解的最后结果.

(3)、请你模仿以上方法尝试对多项式（x²－2x）（x²－2x+2）+1进行因式分解.

查看试题解析
23. 阅读材料
小明遇到这样一个问题：求计算（x+2）（2x+3）（3x+4）所得多项式的一次项系数．

小明想通过计算（x+2）（2x+3）（3x+4）所得的多项式解决上面的问题，但感觉有些繁琐，他想探寻一下，是否有相对简洁的方法．

他决定从简单情况开始，先找（x+2）（2x+3）所得多项式中的一次项系数．通过观察发现：

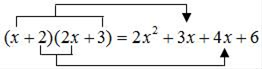
也就是说，只需用x+2中的一次项系数1乘以2x+3中的常数项3，再用x+2中的常数项2乘以2x+3中的一次项系数2，两个积相加1×3+2×2=7，即可得到一次项系数．

延续上面的方法，求计算（x+2）（2x+3）（3x+4）所得多项式的一次项系数．可以先用x+2的一次项系数1，2x+3的常数项3，3x+4的常数项4，相乘得到12；再用2x+3的一次项系数2，x+2的常数项2，3x+4的常数项4，相乘得到16；然后用3x+4的一次项系数3，x+2的常数项2，2x+3的常数项3，相乘得到18．最后将12，16，18相加，得到的一次项系数为46．

参考小明思考问题的方法，解决下列问题：

(1)、计算（2x+1）（3x+2）所得多项式的一次项系数为．

(2)、计算（x+1）（3x+2）（4x﹣3）所得多项式的一次项系数为．

(3)、若计算（x²+x+1）（x²﹣3x+a）（2x﹣1）所得多项式的一次项系数为0，则a= ．

(4)、若x²﹣3x+1是x⁴+ax²+bx+2的一个因式，则2a+b的值为．

查看试题解析