浙教版2019-2020学年初中数学七年级下学期期末复习专题3 整式的乘除

试卷更新日期：2020-07-12 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、x²·x³=x⁶ B、x⁶÷x³=x³ C、x³+x³=2x⁶ D、（-2x）³=-6x³

查看试题解析
2. 要使（﹣6x³）（x²+ax﹣3）的展开式中不含x⁴项，则a＝（）

A、1 B、0 C、﹣1 D、 $\frac{1}{6}$

查看试题解析
3. 若(3x+2)(x+p)=ax²+bx-2，则下列结论正确的是（）

A、a=6 B、b=1 C、p=-2 D、abp=3

查看试题解析
4. 如图，现有正方形卡片A类，B类和长方形卡片C类若干张，若要拼一个长为 $(a + 2 b)$ ，宽为 $(3 a + b)$ 的大长方形，则需要C类卡片（）

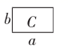A、5张 B、6张 C、7张 D、8张

查看试题解析
5. 有一张边长为 $a$ 的正方形桌面，因实际需要，需将正方形边长增加 $b$ ，木工师傅设计了如图际所示的方案，该方案能验证的等式是（）

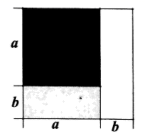A、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ B、 $a^{2} - b^{2} = (a + b) (a - b)$ C、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ D、 $(a + 2 b) (a - b) = a^{2} + a b + b^{2}$

查看试题解析
6. 可以运用平方差公式运算的有（）个
① $(- 1 + 2 x) (- 1 - 2 x)$ ② $(- 1 - 2 x) (1 + 2 x)$ ③ $(a b - 2 b) (- a b - 2 b)$

A、1 B、2 C、3 D、0

查看试题解析
7. 选择计算(-4xy²+3x²y)(4xy²+3x²y)的最佳方法是（）

A、运用多项式乘多项式法则 B、运用平方差公式 C、运用单项式乘多项式法则 D、运用完全平方公式

查看试题解析
8. 已知a＝2 002x＋2 003，b＝2 002x＋2 004，c＝2 002x＋2 005，则多项式a²＋b²＋c²－ab－bc－ca的值为（）

A、0 B、1 C、2 D、3

查看试题解析
9. 纳米是非常小的长度单位，1纳米=10^-7厘米。经研究发现，2019新型冠状病毒(2019-n CoV)的单细胞直径范围为60纳米~140纳米，其最大直径140纳米用科学记数法表示为（）

A、1.40×10^-5厘米 B、140×10^-6厘米 C、1.40×10^-7厘米 D、0.140×10^-4厘米

查看试题解析
10. 若 $({ax}^{m} y^{n}) \div (- 3 x^{2} y^{3}) = 4 x^{3}$ ，则 $a 、 m 、 n$ 取值分别是（）

A、 $- 12 、 6 、 3$ B、 $- 12 、 5 、 3$ C、 $+ 12 、 6 、 9$ D、 $- 12 、 5 、 9$

查看试题解析

二、填空题

11. 计算： ${(- 2020)}^{0} + 3^{- 1} =$ .

查看试题解析
12. 计算： ${(- 0.25)}^{2020} \times 4^{2019} =$ .

查看试题解析
13. 若 ${(- 2 a^{m} b)}^{3} {(\frac{1}{2} a^{n} b^{m})}^{2} = - 2 a^{7} b^{5}$ ，则 $m =$ ， $n =$ .

查看试题解析
14. 下列计算算式中：① ${(- 2 x^{3} y^{2})}^{3} = - 6 x^{9} y^{6}$ ，② $a (a^{2} - 1) = a^{3} - 1$ ，③ ${(- 2)}^{2020} \times {(\frac{1}{2})}^{2019} = 2$ ，④ $(a + b) (a - 2 b) = a^{2} - a b - 2 b^{2}$ ，⑤ $- 2 a \cdot {(a^{2})}^{3} = - 2 a^{9}$ ，正确的是.（填序号）

查看试题解析
15. 已知实数a，b满足ab-3=0，a+b=4，则a-b= 。

查看试题解析
16. 一个长方形的面积为(12ab²-9a²b)，若一边长为3ab，则它的另一边长为。

查看试题解析

三、解答题

17. 若 ${(4 x - 3 y - 5)}^{0}$ 无意义，且3x+2y=8，求x，y的值。

查看试题解析
18. 计算

(1)、-a⁶·a⁵÷a³+(-2a²)⁴-(a⁴)²

(2)、(x-3y)²-4x(2x-y)

(3)、(x-y+z)(x+y+z)

(4)、( $\frac{1}{2}$ )^-3×3^-2+(π-3)⁰÷( $\frac{1}{3}$ )^-1

查看试题解析
19. 计算

(1)、 $a^{m}$ =2, $a^{n}$ =5，求 $a^{2 m - n}$ 的值

(2)、(x+1)(x-p)= $x^{2}$ +qx-3,求 $p^{q}$ 的值．

查看试题解析
20. 化简求值 $(x + 2 y) (x - 2 y) + {(x - 2 y)}^{2} - (6 x^{2} y - 2 x y^{2}) \div (2 y)$ ，其中 $x = - 2$ ， $y = \frac{1}{2}$

查看试题解析
21. 已知，2^m= $a$ ，8ⁿ=b，m、n是正整数，求 $2^{3 m + 6 n}$

查看试题解析
22. 甲乙两人共同计算一道整式乘法： $(2 x + a) (3 x + b)$ ，由于甲抄错了第一个多项式中 $a$ 的符号，得到的结果为 $6 x^{2} + 11 x - 10$ ；由于乙漏抄了第二个多项式中的 $x$ 的系数，得到的结果为 $2 x^{2} - 9 x + 10$ ．请你计算出 $a$ 、 $b$ 的值各是多少，并写出这道整式乘法的符合题意结果．

查看试题解析
23. 已知 $P = 3 x^{2} + m x - \frac{1}{3} y + 4, Q = 2 x - 3 y + 1 - n x^{2}$ ，

(1)、关于 $x, y$ 的式子 $P - 2 Q$ 的取值与字母x的取值无关，求式子 $(m + 3 n) - (3 m - n)$ 的值；

(2)、当 $x \neq 0$ 且 $y \neq 0$ 时,若 $3 P - \frac{1}{3} Q = \frac{35}{3}$ 恒成立，求 $m, n$ 的值。

查看试题解析
24. 好学小东同学，在学习多项式乘以多项式时发现：( $\frac{1}{2}$ x+4)(2x+5)(3x-6)的结果是一个多项式，并且最高次项为： $\frac{1}{2}$ x•2x•3x＝3x³ ，常数项为：4×5×(-6)=-120，那么一次项是多少呢？要解决这个问题，就是要确定该一次项的系数．根据尝试和总结他发现：一次项系数就是： $\frac{1}{2}$ ×5×(-6)+2×(-6)×4+3×4×5＝-3，即一次项为-3x ．
请你认真领会小东同学解决问题的思路，方法，仔细分析上面等式的结构特征．结合自己对多项式乘法法则的理解，解决以下问题．

(1)、计算(x+2)(3x+1)(5x-3)所得多项式的一次项系数为．

(2)、( $\frac{1}{2}$ x+6)(2x+3)(5x-4)所得多项式的二次项系数为．

(3)、若计算(x²+x+1)(x²-3x+a)(2x-1)所得多项式不含一次项，求a的值；

(4)、若(x+1)²⁰²¹=a₀x²⁰²¹+a₁x²⁰²⁰+a₂x²⁰¹⁹+···+a₂₀₂₀x+a₂₀₂₁ ，则a₂₀₂₀= ．

查看试题解析
25. 如果一个正整数能表示为两个连续奇数的平方差，那么我们称这个正整数为“和谐数”，如8=3²-1² ， 16=5²-3² ， 24=7²-5² ，因此，8，16，24这三个数都是“和谐数”．

(1)、在32，75，80这三个数中，是和谐数的是；

(2)、若200为和谐数，即200可以写成两个连续奇数的平方差，则这两个连续奇数的和为；

(3)、小鑫通过观察发现以上求出的“和谐数”均为8的倍数，设两个连续奇数为2n-1和2n+1（其中n取正整数），请你通过运算验证“和谐数是8的倍数”这个结论是否符合题意．

查看试题解析
26. 从边长为a的正方形中剪掉一个边长为b的正方形（如图1），然后将剩余部分拼成一个长方形（如图2）．

(1)、上述操作能验证的等式是（请选择正确的一个）

A、a²-b²=（a+b）（a-b） B、a²-2ab+b²=（a-b）² C、a²+ab=a（a+b）

(2)、若x²-y²=16，x+y=8，求x-y的值；

(3)、计算： $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) \dots (1 - \frac{1}{2018^{2}}) (1 - \frac{1}{2019^{2}})$ ．

查看试题解析
27. 借助图形直观，感受数与形之间的关系，我们常常可以发现一些重要结论．
初步应用

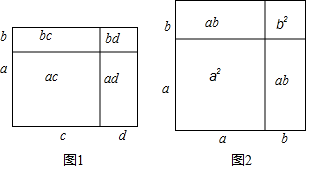(1)、①如图1，大长方形的面积可以看成4个小长方形的面积之和，由此得到多项式乘多项式的运算法，则（用图中字母表示）
②如图2，借助①，写出一个我们学过的公式：（用图中字母表示）

(2)、深入探究
仿照图2，构造图形并计算（a+b+c）²

(3)、拓展延伸
借助以上探究经验，解决下列问题：

①代数式（a₁+a₂+a₂+a₃+a₄+a₅）²展开、合并同类项后，得到的多项式的项数一共有项；

②若正数x、y、z和正数m、n、p，满足x+m=y+n=z+p=t，请通过构造图形比较px+my+nz与t²的大小（画出图形，并说明理由）；

③已知x、y、z满足x+y+z=2m，x²+y²+z²=2n，xyz=p，求x²y²+y²z²+x²z²的值（用含m、n、P的式子表示）

查看试题解析