浙教版2019-2020学年初中数学七年级下学期期末复习专题2 二元一次方程

试卷更新日期：2020-07-12 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列方程中: $① 4 x - 7 = 0$ ； $② 3 x + y = z$ ； $③ x - 7 = x^{2}$ ； $④ 4 x y = 3$ ； $⑤ \frac{x + y}{2} = \frac{y}{3}$ ； $⑥ \frac{3}{x} = 1$ ．属于二元一次方程的个数有（）

A、 $0$ 个 B、 $1$ 个 C、 $2$ 个 D、 $3$ 个

查看试题解析
2. 若 $(a - 2) x^{| a | - 1} + 3 y = 1$ 是关于x、y的二元一次方程，则a=（）

A、1 B、2 C、-2 D、2和-2

查看试题解析
3. 下列方程组中，属于二元一次方程组的是（）

A、 ${\begin{array}{l} x + y = - 3 \\ x + z = - 1 \end{array}$ B、 ${\begin{array}{l} x + y = 3 \\ y = 2 \end{array}$ C、 ${\begin{array}{l} x + y = 3 \\ x^{2} - y = - 3 \end{array}$ D、 ${\begin{array}{l} x + y = 3 \\ x y = - 2 \end{array}$

查看试题解析
4. 下列方程组中，是三元一次方程组的是（）

A、 ${\begin{array}{l} x + y = 0 \\ y + z = 1 \\ z + w = 5 \end{array}$ B、 ${\begin{array}{l} x + y = 0 \\ y + 2 x = 1 \end{array}$ C、 ${\begin{array}{l} 3 x + 4 z = 7 \\ 2 x + 3 y = 9 - z \\ 5 x - 9 y + 7 z = 8 \end{array}$ D、 ${\begin{array}{l} x^{2} - 2 y = 0 \\ y + z = 3 \\ x + y + z = 1 \end{array}$

查看试题解析
5. 已知关于x，y的方程组 ${\begin{cases} 3 x - 5 y = 2 a \\ x - 2 y = a - 5 \end{cases}$ ，则下列结论中正确的个数有（）
①当a=10时，方程组的解是 ${\begin{cases} x = 15 \\ y = 5 \end{cases}$ ；②当x，y的值互为相反数时，a=20；③不存在一个实数a使得x=y；④若3^x-3a=3⁵ ，则a=5

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 用加减消元法解二元一次方程组： ${\begin{cases} x + 3 y = 4 ， ① \\ 2 x - y = 1 ， ② \end{cases}$ 时，下列方法中无法消元的是（）

A、①×2-② B、②×(-3)-① C、①×(-2)+②. D、①-②×3

查看试题解析
7. 解方程组 ${\begin{cases} 3 x + y = 8 (1) \\ x - y = 1 (2) \end{cases}$ ，下列最佳方法是（）

A、代入法消去x，由(2)得：x=1+y B、代入法消去y，由(1)得：y=1-x=0 C、加减法消去x，由(1)-(2)x3得：4y=5 D、加减法消去y，由(1)+(2)得：4x=9

查看试题解析
8. 按如图的运算程序，能使输出结果为3的x、y的值是（）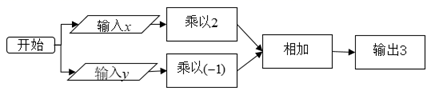

A、 ${\begin{matrix} x = 2 \\ y = 4 \end{matrix}$ B、 ${\begin{matrix} x = 6 \\ y = 12 \end{matrix}$ C、 ${\begin{matrix} x = - 5 \\ y = - 13 \end{matrix}$ D、 ${\begin{matrix} x = - 3 \\ y = - 2 \end{matrix}$

查看试题解析
9. 《九章算术》是中国古代第一部数学专著，它的出现标志着中国古代数学形成了完整的体系，在其方程章中有一道题：“今有五雀，六燕，集称之衡，雀俱重，燕俱轻．一雀一燕交而处，衡适平．并燕雀重一斤．问燕雀一枚各重几何？”其大意是：“现在有5只雀，6只燕，分别集中放在天平上称重，聚在一起的雀重燕轻．将一只雀一只燕交换位置而放，重量相等.5只雀、6只燕重量共一斤，问雀和燕各重多少？”古代记1斤为16两，则设1只雀x两，一只燕y两，可列出方程（）

A、 ${\begin{matrix} 5 x + 6 y = 16 \\ 4 x + y = 5 y + x \end{matrix}$ B、 ${\begin{matrix} 5 x + 6 y = 16 \\ 5 x = 6 y \end{matrix}$ C、 ${\begin{matrix} 5 x + 6 y = 10 \\ 4 x + y = 5 y + x \end{matrix}$ D、 ${\begin{matrix} 5 x + 6 y = 10 \\ 5 x = 6 y \end{matrix}$

查看试题解析
10. 小明在拼图时，发现8个大小一样的小长方形恰好可以拼成一个大的长方形，如图1所示．小红看见了，说“我来试一试”，结果拼成如图2所示的正方形，中间还留有一个洞，恰好是边长为2cm的小正方形．则每个小长方形的长和宽分别为（）．

A、8cm和6cm B、12cm和8cm C、10cm和6cm D、10cm和8cm

查看试题解析

二、填空题

11. 某水果店销售50千克香蕉，第一天售价为9元／千克，第二天降价为6元／千克，第三天再降为3元／千克.三天全部售完，共计所得270元，若该店第二天销售香蕉t千克，则第三天销售香蕉千克.(用含t的代数式表示.)

查看试题解析
12. ${\begin{array}{l} x = 3 \\ y = - 2 \end{array}$ 是二元一次方程 $4 x - 3 y + 2 a - 10 = 0$ 的解，则a= ．

查看试题解析
13. 甲乙两人同解方程组 ${\begin{matrix} a x + b y = 2 \\ c x - 7 y = 8 \end{matrix}$ 时甲正确解得 ${\begin{matrix} x = 3 \\ y = - 2 \end{matrix}$ ，乙因抄错c而得 ${\begin{matrix} x = - 2 \\ y = 2 \end{matrix}$ ，则a+c＝.

查看试题解析
14. 已知a、b都是有理数，观察表中的运算，则m＝.

a、b的运算

a+b

a﹣b

（2a+b）³

运算的结果

﹣4

10

m

查看试题解析
15. 对于问题“若方程组 ${\begin{array}{l} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{array}$ 的解是 ${\begin{array}{l} x = 6 \\ y = 8 \end{array}$ ，求方程组 ${\begin{array}{l} 3 a_{1} x + 2 b_{1} y = 5 c_{1} \\ 3 a_{2} x + 2 b_{2} y = 5 c_{2} \end{array}$ 的解．”有同学提出了把第二个方程组的两个方程的两边都除以5，然后用“换元法”来解决，请用“换元法”求出该方程组的解为．

查看试题解析
16. 中国古代的数学专著《九章算术》有方程组问题“五只雀，六只燕，共重1斤(等于16两)，雀重燕轻．互换其中一只，恰好一样重．”设每只雀、燕的重量各为x两，y两，则根据题意，可得方程组为．

查看试题解析

三、解答题

17. 方程mx+ny=1的两个解是 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ ， ${\begin{array}{l} x = 1 \\ y = 3 \end{array}$ ，求m和n的值．

查看试题解析
18. 已知方程组 ${\begin{array}{l} 2 x + 5 y = - 6 \\ ax-by = - 4 \end{array}$ 和方程组 ${\begin{array}{l} 3 x-5y = 16 ， \\ bx + ay = - 8 \end{array}$ 的解相同，求2a+b的值.

查看试题解析
19. 用指定的方法解方程：

(1)、 ${\begin{cases} x + y = 10 \\ y + 2 x = 0 \end{cases}$ (代入消元法)；

(2)、 ${\begin{cases} 2 x + 5 y = 12 \\ 3 x - 2 y = - 1 \end{cases}$ (加减消元法)

查看试题解析
20. 利用两块完全相同的长方形木块测量一张桌子的高度，首先将木块按图一方式放置，再交换两木块的位置，按图二方式放置，测量数据如图，求桌子的高度.

查看试题解析
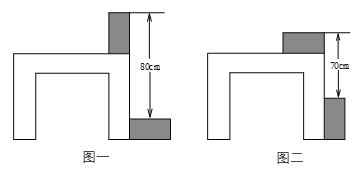
21. 阅读材料：小丁同学在解方程组 ${\begin{cases} \frac{x + y}{3} + \frac{x - y}{5} = 4 \\ \frac{x + y}{3} - \frac{x - y}{5} = - 2 \end{cases}$ 时，他发现：如果直接用代入消元法或加减消元法求解运算量比较大，也容易出错．如果把方程组中的(x+y)看作一个整体，把(x-y)看作一个整体，通过换元，可以解决问题．以下是他的解题过程：
设m=x+y，n=x-y，这时原方程组化为 ${\begin{cases} \frac{m}{3} + \frac{n}{5} = 4 \\ \frac{m}{3} - \frac{n}{5} = - 2 \end{cases}$

解得 ${\begin{cases} m = 3 \\ n = 15 \end{cases}$ ，即 ${\begin{cases} x + y = 3 \\ x - y = 15 \end{cases}$ ，解得 ${\begin{cases} x = 9 \\ y = - 6 \end{cases}$

请你参考小丁同学的做法，解方程组： ${\begin{cases} \frac{2 x + 3 y}{4} + \frac{2 x - 3 y}{3} = 7 \\ \frac{2 x + 3 y}{3} + \frac{2 x - 3 y}{2} = 8 \end{cases}$

查看试题解析
22. 某校举办“迎冬奥会“学生书画展览，现要在长方形展厅中划出3个形状、大小完全一样的小长方形(图中阴影部分)区域摆放作品．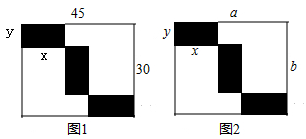

(1)、如图1，若大长方形的长和宽分别为45米和30米，设小长方形的长为x，宽为y，求出x和y的值．

(2)、如图2，若大长方形的长和宽分别为a和b．
①求出1个小长方形周长与大长方形周长之比；

②若作品展览区域(阴影部分)面积占展厅面积的 $\frac{1}{3}$ ，求x和y的数量关系．

查看试题解析
23. 一家商店进行门店升级需要装修，装修期间暂停营业，若请甲乙两个装修组同时施工，8天可以完成，需付费用共3520元；若先请甲组单独做6天，再请乙组单独做12天可以完成，需付费用3480元，问：

(1)、甲、乙两组工作一天，商店各应付多少钱？

(2)、已知甲组单独完成需12天，乙组单独完成需24天，单独请哪个组，商店所需费用最少？

(3)、装修完毕第二天即可正常营业，且每天仍可盈利200元(即装修前后每天盈利不变)，你认为商店应如何安排施工更有利？说说你的理由．(可用（1）（2）问的条件及结论)

查看试题解析
24. 如图1是某机场的平地电梯，电梯AB的长度为120米，如图2所示.若两人不乘电梯在地面匀速行走，小明每分钟的路程是小王的1.5倍，且1.5分钟后，小明比小王多行走30米.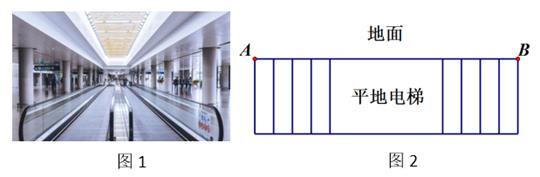

(1)、求两人在地面上每分钟各行走多少米？

(2)、若两人在平地电梯上行走，电梯向前行驶，两人也同时在电梯上行走.当小明到达B处时，小王还剩 $\frac{80}{3}$ 米.
①求平地电梯每分钟行驶多少米？

②当小明到达B处时，发现有一袋行李忘在A处，同时关注此时为7点55分，小明马上从地面返回A处，拿了行李后立即乘平地电梯（同时行走）去B处.问小明能否在8点前和小王汇合，并说明理由.

查看试题解析

a、b的运算	a+b	a﹣b	（2a+b）³
运算的结果	﹣4	10	m