2020年暑期衔接训练青岛版数学八年级下册:第3讲 三角形的中位线定理
试卷更新日期:2020-07-12 类型:复习试卷
一、单选题
-
1. 如图,点D、E、F分别是△ABC的边AB、BC、CA的中点,连接DE、EF、FD得△DEF,如果△ABC的周长是24cm,那么△DEF的周长是( )
 A、6cm B、12cm C、18cm D、32cm2. 如图是一块等腰三角形空地ABC,已知点D,E分别是边AB,AC的中点,量得AC=10米,AB=BC=6米,若用篱笆围成四边形BCED来放养小鸡,则需要篱笆的长是( )
A、6cm B、12cm C、18cm D、32cm2. 如图是一块等腰三角形空地ABC,已知点D,E分别是边AB,AC的中点,量得AC=10米,AB=BC=6米,若用篱笆围成四边形BCED来放养小鸡,则需要篱笆的长是( ) A、22米 B、17米 C、14米 D、11米3. 如图,已知四边形ABCD中,R、P分别是BC、CD上的点,E、F分别是AP、RP的中点,当点P在CD上从C向D移动而点R不动时,那么下列结论成立的是( )
A、22米 B、17米 C、14米 D、11米3. 如图,已知四边形ABCD中,R、P分别是BC、CD上的点,E、F分别是AP、RP的中点,当点P在CD上从C向D移动而点R不动时,那么下列结论成立的是( ) A、线段EF的长逐渐增大 B、线段EF的长逐渐减小 C、线段EF的长不变 D、线段EF的长与点P的位置有关4. 如图,四边形ABCD中,点E、F、G分别是线段AD、BC、AC的中点,则△EFG的周长( )
A、线段EF的长逐渐增大 B、线段EF的长逐渐减小 C、线段EF的长不变 D、线段EF的长与点P的位置有关4. 如图,四边形ABCD中,点E、F、G分别是线段AD、BC、AC的中点,则△EFG的周长( ) A、与AB,BC,AC的长有关 B、与AD,DC,AC的长有关 C、与AB,DC,EF的长有关 D、与AD,BC,EF的长有关5. 如图,在△ABC中,BD、CE是△ABC的中线,BD与CE相交于点0,点F、G分别是BO、CO的中点,连接AO.若AO=6cm,BC=8cm,则四边形DEFG的周长是( )
A、与AB,BC,AC的长有关 B、与AD,DC,AC的长有关 C、与AB,DC,EF的长有关 D、与AD,BC,EF的长有关5. 如图,在△ABC中,BD、CE是△ABC的中线,BD与CE相交于点0,点F、G分别是BO、CO的中点,连接AO.若AO=6cm,BC=8cm,则四边形DEFG的周长是( ) A、14 cm B、18 cm C、24 cm D、28 cm6. 直角三角形斜边上的中线与连结两直角边中点的线段的关系是( )
A、14 cm B、18 cm C、24 cm D、28 cm6. 直角三角形斜边上的中线与连结两直角边中点的线段的关系是( )
A、相等且平分 B、相等且垂直 C、垂直平分 D、垂直平分且相等7. 如图,点D、E、F分别是△ABC中AB、BC、AC边上的中点,点M、N、P分别是DE、EF、DF的中点.若△ABC的周长为24,则△PMN的周长为( ) A、6 B、8 C、10 D、128. 如图,△ABC的周长为26,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P.若BC=10,则PQ的长是( )
A、6 B、8 C、10 D、128. 如图,△ABC的周长为26,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P.若BC=10,则PQ的长是( ) A、1.5 B、2 C、3 D、49. 如图,四边形ABCD中,AB与CD不平行,M,N分别是AD,BC的中点,AB=4,DC=2,则MN的长不可能是( )
A、1.5 B、2 C、3 D、49. 如图,四边形ABCD中,AB与CD不平行,M,N分别是AD,BC的中点,AB=4,DC=2,则MN的长不可能是( ) A、3 B、2.5 C、2 D、1.510. 如图,以任意△ABC的边AB和AC向形外作等腰Rt△ABD和等腰Rt△ACE,F、G分别是线段BD和CE的中点,则的值等于( )
A、3 B、2.5 C、2 D、1.510. 如图,以任意△ABC的边AB和AC向形外作等腰Rt△ABD和等腰Rt△ACE,F、G分别是线段BD和CE的中点,则的值等于( )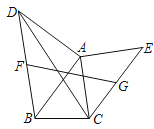 A、 B、 C、 D、11. 如图,在△ABC中,D,E,F分别为BC,AC,AB边的中点,AH⊥BC于H,FD=8,则HE等于( )
A、 B、 C、 D、11. 如图,在△ABC中,D,E,F分别为BC,AC,AB边的中点,AH⊥BC于H,FD=8,则HE等于( ) A、20 B、16 C、12 D、812. 如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )
A、20 B、16 C、12 D、812. 如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )
A、1 B、2 C、3 D、4二、填空题
-
13. 如图所示,DE为 的中位线,点F在DE上,且 ,若 , ,则 的长为.
 14. 如图,在四边形 中,点E、F分别是线段AD、BC的中点,G、H分别是线段BD、AC的中点,当四边形 的边满足时,四边形 是菱形.
14. 如图,在四边形 中,点E、F分别是线段AD、BC的中点,G、H分别是线段BD、AC的中点,当四边形 的边满足时,四边形 是菱形. 15. 已知:如图,在△ABC中,点A1 , B1 , C1分别是BC、AC、AB的中点,A2 , B2 , C2分别是B1C1 , A1C1 , A1B1的中点,依此类推….若△ABC的周长为1,则△AnBnCn的周长为.
15. 已知:如图,在△ABC中,点A1 , B1 , C1分别是BC、AC、AB的中点,A2 , B2 , C2分别是B1C1 , A1C1 , A1B1的中点,依此类推….若△ABC的周长为1,则△AnBnCn的周长为.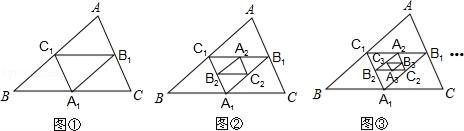 16. 如图是跷跷板的示意图,立柱 与地面垂直,以 为横板 的中点, 绕点 上下转动,横板 的 端最大高度 是否会随横板长度的变化而变化呢?一位同学做了如下研究:他先设 , ,通过计算得到此时的 ,再将横板 换成横板 , 为横板 的中点,且 ,此时 点的最大高度为 ,由此得到 与 的大小关系是: (填“ 、“ ”或“ ”)可进一步得出, 随横板的长度的变化而(填“不变”或“改变”).
16. 如图是跷跷板的示意图,立柱 与地面垂直,以 为横板 的中点, 绕点 上下转动,横板 的 端最大高度 是否会随横板长度的变化而变化呢?一位同学做了如下研究:他先设 , ,通过计算得到此时的 ,再将横板 换成横板 , 为横板 的中点,且 ,此时 点的最大高度为 ,由此得到 与 的大小关系是: (填“ 、“ ”或“ ”)可进一步得出, 随横板的长度的变化而(填“不变”或“改变”).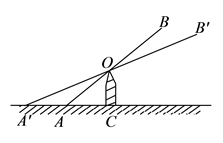 17. 如图,在三角形ABC中,∠ACB=90°,M,N分别是AB、AC的中点,延长BC至点D,使CD= BD,连结DM、DN、MN。若AB=5,则DN=。
17. 如图,在三角形ABC中,∠ACB=90°,M,N分别是AB、AC的中点,延长BC至点D,使CD= BD,连结DM、DN、MN。若AB=5,则DN=。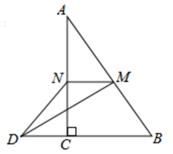 18. 如图,∠ACB=90°,D为AB的中点,连接DC并延长到E,使CE=CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为
18. 如图,∠ACB=90°,D为AB的中点,连接DC并延长到E,使CE=CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为 19. 如图,△ABC中,AB=AC,以AC为斜边作Rt△ADC,使∠ADC=90°,∠CAD=∠CAB=26°,E、F分别是BC、AC的中点,则∠EDF等于
19. 如图,△ABC中,AB=AC,以AC为斜边作Rt△ADC,使∠ADC=90°,∠CAD=∠CAB=26°,E、F分别是BC、AC的中点,则∠EDF等于 20. 如图,在△ABC中,AB=4,AC=3,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为
20. 如图,在△ABC中,AB=4,AC=3,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为
三、解答题
-
21. 如图,在△ABC中,AD是BC边上的中线,点F在AC上,AF=FC,AD与BF交于点E.求证:点E是AD的中点.
 22. 【知识链接】连接三角形两边中点的线段,叫做三角形的中位线
22. 【知识链接】连接三角形两边中点的线段,叫做三角形的中位线【动手操作】小明同学在探究证明中位线性质定理时,是沿着中位线将三角形剪开然后将他们无缝隙、无重叠
的拼在一起构成平行四边形,从而得出:三角形中位线平行于第三边且等于第三边的一半
【定理证明】小明为证明定理,画出了图形,写出了不完整的已知和求证(如图1);
 (1)、在图1方框中填空,以补全已知和求证;(2)、按图2小明的想法写出证明.23. 如图,四边形ABCD中,已知AB=CD,点E、F分别为AD、BC的中点,延长BA、CD,分别交射线FE于P、Q两点.求证:∠BPF=∠CQF.
(1)、在图1方框中填空,以补全已知和求证;(2)、按图2小明的想法写出证明.23. 如图,四边形ABCD中,已知AB=CD,点E、F分别为AD、BC的中点,延长BA、CD,分别交射线FE于P、Q两点.求证:∠BPF=∠CQF. 24. D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
24. D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?(直接写出答案,不需要说明理由.)


