2020年暑期衔接训练人教版数学七年级下册：第13讲 平面直角坐标系
试卷更新日期：2020-07-11 类型：复习试卷
一、单选题
-
1. 已知线段AB与x轴平行，点A坐标为(3，2)，AB=4，则点B的坐标为（ ）A、(7，2) B、(-1，2)或(7，2) C、(3，6) D、(3，6)或(3，-2)2. 已知点A(2，1)，过点A作x轴的垂线，垂足为C，则点C的坐标为（ ）．A、(1，2) B、（1，0） C、（0，1） D、（2，0）3. 已知y轴上点P到x轴的距离为3，则点P坐标为（ ）A、(0，3) B、(3，0) C、(0，3)或(0，-3) D、(3，0)或(-3，0)4. 已知点M（a﹣2，a+1）在x轴上，则点M的坐标为（ ）A、（0，3） B、（﹣1，0） C、（﹣3，0） D、无法确定5. 如图，在中国象棋棋盘中，如果将“卒”的位置记作（3，1），那么“相”的位置可记作（ ）
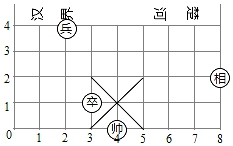A、（2，8） B、（2，4） C、（8，2） D、（4，2）6. 若点 在第四象限，且到 轴， 轴的距离分别是2和3，则点 的坐标为（ ）A、 B、 C、 D、7. 如图，若在象棋盘上建立直角坐标系xOy，使“帥”位于点（-1，-2），“馬”位于点（2，-2），则“兵”位于点（ ）
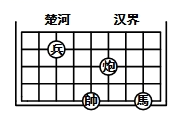A、（-2，3） B、（-2，1） C、（-3，1） D、（-3，3）8. 如图，在平面直角坐标系中，A(1，1)， B(-1，1)， C(-1，-2)，D(1，-2)，把一条长为 2021 个单位长度且没有弹性的细线(线的粗细不略不计)的一端固定在点 A 处， 并按 A﹣B﹣C﹣D﹣A﹣的规律绕在四边形 ABCD 的边上，则细线另一端所在位置的点的坐标是（ ）
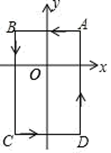A、(1，0) B、(1，1) C、(0，1) D、( -1， - 2)二、填空题
-
9. 若点P（a－4，2a－6）在x轴上，则点P的坐标为 ．10. 已知AB//y轴，A点的坐标为(3，2)，并且AB=5，则B的坐标为 ．11. 如图，各个小正方形格子的边长均为 1，图中 A，B 两点的坐标分别为（－3，5），（3，5），则点 C 在同一坐标系下的坐标为 ．
12. 若 的坐标为 ，且点 到 轴的距离是1，则点 的坐标是.13. 如图所示，△ABC三个顶点的坐标分别是A（ ， ）、B（ ， ）、C（ ， ）．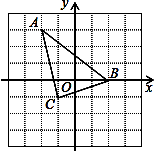
14. 在平面直角坐标系中，y轴的左侧有一点P(x ， y)，且满足 =2， =9，则点P的坐标是.15. 如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“ ”方向排列，如 ， ， ， ， ， ， .根据这个规律探索可得，第110个点的坐标为.
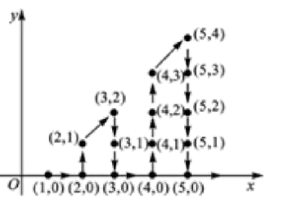16. 在平面直角坐标系中，对于P（x，y）作变换得到P（﹣y+1，x+1），例如：A1（3，1）作上述变换得到A2（0，4），再将作上述变换得到A3（﹣3，1），这样依次得到A2 ， A3 ， A1 ， …，A0 ， ……，则A2020的坐标是.三、解答题
-
17. 已知： 的三个顶点坐标 ， ， ，在平面直角坐标系中画出 ，并求 的面积．
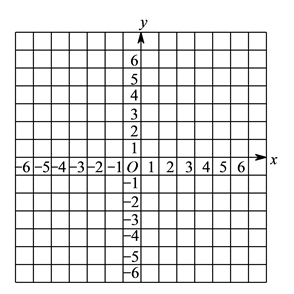18. 已知平面直角坐标中有一点M（2﹣a，3a+6），点M到两坐标轴的距离相等，求M的坐标．四、综合题
