2020年暑期衔接训练人教版数学七年级下册:第2讲 垂线
试卷更新日期:2020-07-11 类型:复习试卷
一、单选题
-
1. 如图,已知直线 AB,CD 相交于点 O,EF⊥AB 于点 O,若∠BOC=55°,则∠DOF=( )
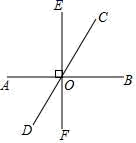 A、35° B、45° C、55° D、90°2. 如图,把小河里的水引到田地A处就作AB⊥l,垂足为B,沿AB挖水沟,水沟最短,理由是( )
A、35° B、45° C、55° D、90°2. 如图,把小河里的水引到田地A处就作AB⊥l,垂足为B,沿AB挖水沟,水沟最短,理由是( ) A、垂线段最短 B、两点确定一条直线 C、点到直线的距离 D、两点之间线段最短3. 如图,点P在直线l外,点A,B在直线l上,PA=3,PB=7,点P到直线l的距离可能是( )
A、垂线段最短 B、两点确定一条直线 C、点到直线的距离 D、两点之间线段最短3. 如图,点P在直线l外,点A,B在直线l上,PA=3,PB=7,点P到直线l的距离可能是( ) A、2 B、4 C、7 D、84. 过一点画已知直线的垂线,可画垂线的条数是( )A、0 B、1 C、2 D、无数5. 如图,A是直线l外一点,点B,E,D,C在直线l上,且 ,D为垂足,如果量得 , , , ,则点A到直线l的距离为( )
A、2 B、4 C、7 D、84. 过一点画已知直线的垂线,可画垂线的条数是( )A、0 B、1 C、2 D、无数5. 如图,A是直线l外一点,点B,E,D,C在直线l上,且 ,D为垂足,如果量得 , , , ,则点A到直线l的距离为( ) A、11 cm B、7 cm C、6 cm D、5 cm6. 点P为直线外一点,点A、B在直线l上,若PA=4cm,PB=5cm,则点P到直线l的距离是( )A、4cm B、小于4cm C、不大于4cm D、5cm7. 下列图形中,线段AD的长表示点A到直线BC距离的是( )
A、11 cm B、7 cm C、6 cm D、5 cm6. 点P为直线外一点,点A、B在直线l上,若PA=4cm,PB=5cm,则点P到直线l的距离是( )A、4cm B、小于4cm C、不大于4cm D、5cm7. 下列图形中,线段AD的长表示点A到直线BC距离的是( )
A、 B、
B、 C、
C、 D、
D、 8. 如图,平行河岸两侧各有一城镇P,Q,根据发展规划,要修建一条公路连接P,Q两镇.已知相同长度造桥总价远大于陆上公路造价,为了尽量减少总造价,应该选择方案( )
8. 如图,平行河岸两侧各有一城镇P,Q,根据发展规划,要修建一条公路连接P,Q两镇.已知相同长度造桥总价远大于陆上公路造价,为了尽量减少总造价,应该选择方案( )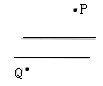 A、
A、 B、
B、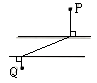 C、
C、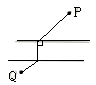 D、
D、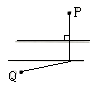 9. 已知点P为直线m外一点,点A,B,C为直线m上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线m的距离为( )A、4 cm B、5 cm C、小于2 cm D、不大于2 cm10.
9. 已知点P为直线m外一点,点A,B,C为直线m上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线m的距离为( )A、4 cm B、5 cm C、小于2 cm D、不大于2 cm10.
在下列语句中,正确的是( ).
A、在平面上,一条直线只有一条垂线; B、过直线上一点的直线只有一条; C、过直线上一点且垂直于这条直线的直线有且只有一条; D、垂线段的长度就是点到直线的距离二、填空题
-
11. 如图,小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段的长度.
 12. 如图,连接直线l外一点P与直线l上各点O,A1 , A2 , A3 , …,其中PO⊥l,这些线段PO,PA1 , PA2 , PA3 , …中,最短的线段是 .
12. 如图,连接直线l外一点P与直线l上各点O,A1 , A2 , A3 , …,其中PO⊥l,这些线段PO,PA1 , PA2 , PA3 , …中,最短的线段是 . 13. 如图是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段BN的长度,这样测量的依据是 .
13. 如图是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段BN的长度,这样测量的依据是 .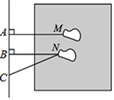 14. 如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠AOE=55°,则∠BOD的度数为.
14. 如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠AOE=55°,则∠BOD的度数为. 15. 如图,直线AB、CD相交于点O,∠COE为直角,∠AOE=60°,则∠BOD=°.
15. 如图,直线AB、CD相交于点O,∠COE为直角,∠AOE=60°,则∠BOD=°. 16. 如图,直线AB,CD相交于点O,射线OE⊥CD, 给出下列结论:①∠2和∠4互为对顶角;②∠3+∠2=180°;③∠5与∠4互补;④∠5=∠3-∠1;其中正确的是。(填序号)
16. 如图,直线AB,CD相交于点O,射线OE⊥CD, 给出下列结论:①∠2和∠4互为对顶角;②∠3+∠2=180°;③∠5与∠4互补;④∠5=∠3-∠1;其中正确的是。(填序号)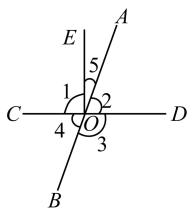 17. 如图,已知直线AD、BE、CF相交于O,OG⊥AD,且∠BOC=35°,∠FOG=30°,则∠DOE= .
17. 如图,已知直线AD、BE、CF相交于O,OG⊥AD,且∠BOC=35°,∠FOG=30°,则∠DOE= .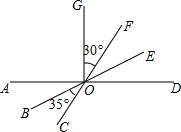 18. 如图,∠1=15°,∠AOC=90°.若点B,O,D在同一条直线上,则∠2= .
18. 如图,∠1=15°,∠AOC=90°.若点B,O,D在同一条直线上,则∠2= .
三、解答题
-
19. 如图,直线AB,CD,EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=28°,求∠BOE,∠AOG的度数.
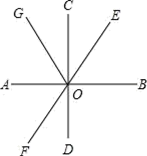 20. 如图,直线AB、CD相交于点O,EO⊥AB,垂足为O,∠EOC:∠AOD=7:11,求∠DOE的度数.
20. 如图,直线AB、CD相交于点O,EO⊥AB,垂足为O,∠EOC:∠AOD=7:11,求∠DOE的度数.