苏教版高中数学必修一3.3幂函数
试卷更新日期:2020-07-10 类型:同步测试
一、单选题
-
1. 若幂函数 的图象过点 ,则函数 的最大值为( )A、1 B、 C、2 D、2. 下图给出四个幂函数的图象,则图象与函数的大致对应是 ( )
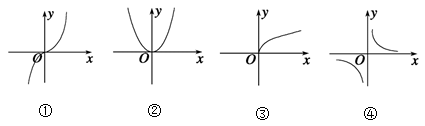 A、①
A、①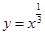 ,②
,②  ,③
,③ 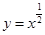 ,④
,④ 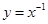 B、①
B、① 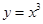 ,②
,②  ,③
,③ 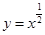 ,④
,④ 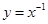 C、①
C、①  ,②
,② 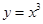
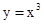 ,③
,③ 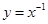 ,④
,④ 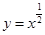 D、①
D、① 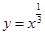 ,②
,② 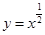 ,③
,③  ,④
,④ 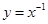 3. 已知幂函数f(x)=(n2+2n-2) (n∈Z)的图像关于y轴对称,且在(0,+∞)上是减函数,则n的值为( )A、1 B、2 C、1或2 D、1或-34. 设 , , ,则下列正确的是( )A、 B、 C、 D、5. 当 时,幂函数y=xα的图象不可能经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 下列函数:①y=x2+1;②
3. 已知幂函数f(x)=(n2+2n-2) (n∈Z)的图像关于y轴对称,且在(0,+∞)上是减函数,则n的值为( )A、1 B、2 C、1或2 D、1或-34. 设 , , ,则下列正确的是( )A、 B、 C、 D、5. 当 时,幂函数y=xα的图象不可能经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 下列函数:①y=x2+1;② ;③y=2x2;④
;③y=2x2;④  ;⑤
;⑤  ,其中幂函数是( )
,其中幂函数是( )
A、①⑤ B、①②③ C、②④ D、②③⑤7. 若函数f(x)是幂函数,且满足 ,则 的值为( )A、-3 B、 C、3 D、8. 函数y=xa , y=xb , y=xc的图像如图所示,则实数a、b、c的大小关系为( ) A、c<b<a B、a<b<c C、b<c<a D、c<a<b9. 下列结论中,正确的是( )
A、c<b<a B、a<b<c C、b<c<a D、c<a<b9. 下列结论中,正确的是( )
A、幂函数的图象都通过点(0,0),(1,1) B、幂函数的图象可以出现在第四象限 C、当幂指数α取1,3, 时,幂函数y=xα是增函数 D、当幂指数α=-1时,幂函数y=xα在定义域上是减函数10. 若 ,则下列结论正确的是( )A、 B、 C、 D、11. 已知幂函数f(x)= ,若f(a+1)<f(10-2a),则a的取值范围是( )A、(3,5) B、(-1,+∞) C、(-∞,5) D、(-1,5)12. 函数 是幂函数,对任意 ,且 ,满足 ,若 ,且 的值为负值,则下列结论可能成立的是( )A、 B、
B、 C、
C、 D、以上都可能
13. 四人赛跑,假设其跑过的路程和时间的函数关系分别是f1(x)=x2 , f2(x)=4x , f3(x)=log2x , f4(x)=2x如果他们一直跑下去,最终跑在最前面的人具有的函数关系是( )A、f1(x)=x2 B、f2(x)=4x C、f3(x)=log2x D、f4(x)=2x
D、以上都可能
13. 四人赛跑,假设其跑过的路程和时间的函数关系分别是f1(x)=x2 , f2(x)=4x , f3(x)=log2x , f4(x)=2x如果他们一直跑下去,最终跑在最前面的人具有的函数关系是( )A、f1(x)=x2 B、f2(x)=4x C、f3(x)=log2x D、f4(x)=2x二、填空题
-
14. 一种产品的产量原来为a,在今后m年内,计划使产量每年比上一年增加p%,则产量y随年数x变化的函数解析式为 , 定义域为 .15. 已知 是幂函数,且 在定义域上单调递增,则 .
16. 幂函数 的图象过点 ,那么 .17. 已知幂函数 的图象关于原点对称且与x轴、y轴均无交点,则整数m的值为 .18. 幂函数 的单调增区间是19. 已知点( ,2)在幂函数y=f(x)的图象上,点(﹣2, )在幂函数y=g(x)的图象上,则f(2)+g(﹣1)= .
三、解答题
-
20. 已知幂函数y=f(x)的图象过点
 .
(1)、求函数f(x)的解析式(2)、记g(x)=f(x)+x , 判断g(x)在(1,+∞)上的单调性,并证明之.21. 已知幂函数f(x)=(m3﹣m+1)x (m∈Z)的图象与x轴,y轴都无交点,且关于y轴对称(1)、求f(x)的解析式;(2)、解不等式f(x+1)>f(x﹣2)22. 函数f(x)=是偶函数.
.
(1)、求函数f(x)的解析式(2)、记g(x)=f(x)+x , 判断g(x)在(1,+∞)上的单调性,并证明之.21. 已知幂函数f(x)=(m3﹣m+1)x (m∈Z)的图象与x轴,y轴都无交点,且关于y轴对称(1)、求f(x)的解析式;(2)、解不等式f(x+1)>f(x﹣2)22. 函数f(x)=是偶函数.(1)试确定a的值,及此时的函数解析式;
(2)证明函数f(x)在区间(﹣∞,0)上是减函数;
(3)当x∈[﹣2,0]时,求函数f(x)=的值域.
23. 已知函数f(x)=(m2﹣m﹣1)x﹣5m﹣3 , m为何值时,f(x):(1)、是幂函数;(2)、是正比例函数;(3)、是反比例函数;(4)、是二次函数.